Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої
Розділ 2. Взаємне розміщення прямих па площині
§ 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої
128. m ⊥ n, MN ⊥ АВ.
129.
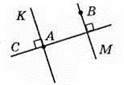
KA ⊥ c, ВМ ⊥ с.
130.
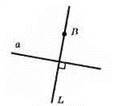
ВL ⊥ a.
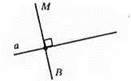
MВ ⊥ a.
131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b.
2) Промінь ЕА і відрізок СМ перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b.
3) Відрізки AB і DE не перпендикулярні, оскільки вони обидва лежать
4) Промені CN і СЕ перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b.
132. 1) Відрізки DE і CN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b.
2) Промені СМ і СА перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b.
3) Промінь СЕ і відрізок СА не перпендикулярні, оскільки вони обидва лежать на прямій а.
4) Відрізки BD і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a i b.
133.

Встановимо косинець так, щоб одна із сторін прямого кута співпала з прямою а, а на другій знайдемо 2,5 см. Відмітимо
134.
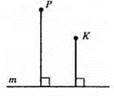
Встановимо косинець так, щоб одна із сторін прямого кута співпала з прямою m, а на другій знайдемо 3 см. Відмітимо точку Р. Аналогічно для точки К.
135.
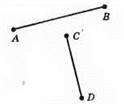
Проведемо довільний відрізок AB. Встановимо косинець так, щоб одна сторона прямого кута збіглася з відрізком AB. По другій стороні прямого кута на деякій відстані від AB проведемо довільний відрізок CD.
136.
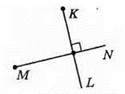
Довільно проведемо промінь MN. За допомогою косинця проведемо промінь KL.
137. 1) Дві прямі перпендикулярні, якщо вони перетинаються під прямим кутом.
∠AON = ∠AOK + ∠KON = 25° + 66° = 91°. Отже, прямі AB і MN не перпендикулярні.
2) ∠BON = ∠LON – ∠LOB = 118° – 28° = 90°. Отже, прямі AB і MN перпендикулярні.
138. 1) Дві прямі перпендикулярні, якщо вони перетинаються під прямим кутом.
∠MOA = ∠MOK – ∠AOK = 122° – 31° = 91°. Отже, прямі AB і MN не перпендикулярні.
2) ∠MOB = ∠MOL + ∠LOB = 59° + 31° = 90°. Отже, прямі AВ і MN перпендикулярні.
140. 1) Оскільки AB ⊥ CD, то ∠AOD = 90°.
∠AOD = ∠AOM + ∠MOD. Звідси ∠MOD = ∠AOD – ∠AOM, ∠AOM = ∠NOB = 25° (яке вертикальні кути). Отже, ∠MOD = 90° – 25° = 65°.
Відповідь: 65°.
2) Оскільки AB ⊥ CD, то ∠BOD = 90°. ∠MOB = ∠MOD + ∠BOD. Звідси ∠MOD = ∠MOB – ∠BOD. ∠MOD = 150° – 90° = 60°. ∠CON = ∠MOD = 60° (як вертикальні кути).
Відповідь: 60°.
141. 1) Оскільки КL ⊥ MN, то ∠LON = 90°. ∠KOP і ∠FOL – вертикальні. За властивістю вертикальних кутів ∠KOP = ∠FOL. Знайдемо ∠FOL.
∠NOF = ∠LON + ∠FOL, звідси ∠FOL = ∠NOF – ∠LON = 140° – 90° = 50°. Звідси ∠KOP = 50°.
Відповідь: 50°.
2) Оскільки KL ⊥ MN, то ∠KOM = 90°. ∠KOF = ∠KOM + ∠MOF.
∠MOF = ∠PON = 37° (як вертикальні кути). Отже, ∠KOF = 90° + 37° = 127°.
Відповідь: 127°.
142. Промінь СВ – спільна сторона кутів ABC та СВМ. Знайдемо суму цих кутів.
∠AВС + ∠CBM = 90° + 90° = 180°. Отже, ці кути суміжні.
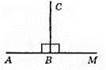
За означенням не спільні сторони суміжних кутів – доповняльні промені. Отже, точки А, В і М лежать на одній прямій.
143.
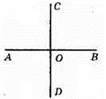
Позначимо кожен з двох суміжних кутів, що утворилися, х. Тоді за властивістю суміжних кутів х + х = 180°, 2х = 180°, х = 90°.
Отже, кут, під яким перетинаються прямі, прямий. Тоді прямі – перпендикулярні.
144.
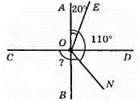
Оскільки AB ⊥ CD, то ∠COB = 90°. ∠АОВ = ∠AOE + ∠EON + ∠BON. Звідси ∠BON = ∠AOB – (∠AOE + ∠EON) = 180° – (20° + 110°) = 180° – 130° = 50°. ∠CON = ∠COB + ∠BON = 90°+ 50° = 140°.
145.
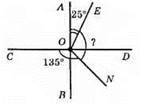
Оскільки AB ⊥ CD, то ∠COB = 90°. ∠CON = ∠COB + ∠BON. Звідси ∠BON = ∠CON – ∠COB = 135° – 90° = 45°.
∠АОВ = ∠AOE + ∠EON + ∠BON. Звідси ∠EON = ∠AOB – (∠AOE + ∠BON) = 180° – (25° + 45°) = 110°.
Відповідь: 110°.
146.
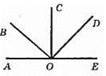
∠AOE – розгорнутий кут, ∠AOE = 180°. ∠AOE = ∠AOB + ∠BOC + ∠COD + ∠DOE = 180°. Оскільки ∠AOB = ∠COD, ∠BOC = ∠DOE, TO 2(∠AOB + ∠BOC) = 180°, ∠AOB + ∠BOC = 90°. Отже, ОС ⊥ AE. 2(∠BOC + ∠COD) = 180°, ∠BOC + ∠COD = 90°. Отже, BO ⊥ OD.
147.
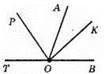
Нехай ∠AOB – заданий кут, OK – бісектриса кута АОВ. PO ⊥ OK, отже, ∠POK = 90°. ∠TOB – розгорнутий кут, ∠TOB = 180°. ∠TOB = ∠TOP + ∠POA + ∠LAOK + ∠KOB = 180°. Оскільки ∠POK = 90°,то ∠POA + ∠AOK = 90°, ∠TOP + 90° + ∠KOB = 180°, звідси ∠TOP + ∠KOB = 90°. Якщо ∠KOB = ∠AOK, TO ∠TOP = ∠POА. Отже, OP – бісектриса кута TOA.
148.
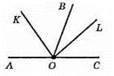
OK – бісектриса кута AOB, OL – бісектриса кута BOC. OK ⊥ OL, отже, ∠KOB + ∠BOL = 90°. Оскільки ∠AOK = ∠KOB, ∠BOL = ∠LOC, то ∠AOK + ∠LOC = 90°. ∠AOC = ∠AOK + ∠KOB + ∠BOL + ∠LOC = 180°. Отже, OA і ОС – доповняльні промені, OB – спільна сторона кутів АОВ і ВОС, тобто ∠AOB і ∠BOC – суміжні.
149. 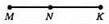
MK = MN + NK, MK = 3 CM 2MM + 4,1 CM; 3 CM 2 MM = 3,2 CM; MK = 3,2 CM + 4,1 CM = 7,3 CM.
2) 2 CM 5 MM = 2,5 CM; MK = MN + NK, звідси MN = MK + NK = 7,8 CM – 2,5 CM = 5,3 CM.
Відповідь: 1) 7,3 CM; 2) 5,3 CM.
150. Нехай один із суміжних кутів х, тоді другий х + 36. Оскільки сума суміжних кутів дорівнює 180°, маємо: х + х + 36° = 180°; 2х = 144°; х = 72°.
Отже, один із кутів дорівнює 72°, другий – 180° – 72° = 108°.
Відповідь: 72°, 108°.
151. Периметр прямокутника дорівнює 32 см, отже, сума двох його сторін дорівнює 16 см. Розглянемо випадки:
Ширина (см) | Довжина (см) | Площа (см2) |
1 | 15 | 15 |
2 | 14 | 28 |
3 | 13 | 39 |
4 | 12 | 48 |
5 | 11 | 55 |
6 | 10 | 60 |
7 | 9 | 63 |
8 | 8 | 64 |
Отже, площа прямокутника може дорівнювати 55 см2, 60 см2, 64 см2.
Відповідь: 55 см2, 60 см2, 64 см2.