Показникові рівняння
УРОК 45
Тема. Показникові рівняння
Мета уроку. Формування умінь учнів розв’язувати найпростіші показникові рівняння.
І. Перевірка домашнього завдання
1. Учитель відповідає на питання учнів, що виникли в процесі виконання домашніх завдань.
2. Самостійна робота
Початковий рівень (2 бали) | |
1) Які з поданих функцій у = 5х; | |
Зростаючими? | Спадними? |
Середній рівень | |
2) Порівняйте числа: | |
А) | А) |
Б) | Б) |
Достатній рівень (3 бали) | |
3) Знайдіть множину значень функції: | |
|
|
Високий рівень (4 бали) | |
4) Побудуйте графік функції | |
| У = |2-х – 2|. |
Відповіді: | |
1 1. Функції у = 5х, 2. a) Оскільки функція у = 0,115х спадна і Б) Оскільки – | 2 варіант. 1. Функції 2. a) Оскільки Б) Оскільки – |
3. Оскільки | 3. |
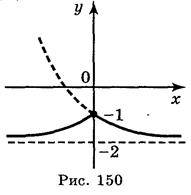
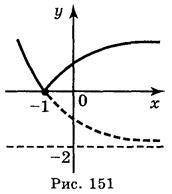
4. (Рис. 150) | 4. (Рис. 151) |
II. Сприймання і усвідомлення нового матеріалу
Показниковими називаються рівняння, у яких невідоме міститься в показнику степеня при постійних основах.
Наприклад. Рівняння 2х + 3 = 0; 3х+1 – 3х – 1 = 0 є показниковими.
Найпростішим показниковим рівнянням є рівняная ах = b, де а > 0, а? 1, Оскільки множина значень функції у = aх – множина додатних чисел, то рівняння aх = b:
1) має один корінь, якщо b > 0 (рис. 152);
2) не має коренів, якщо b < 0 (рис. 153).
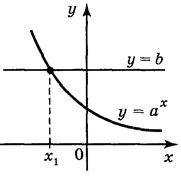
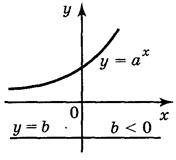
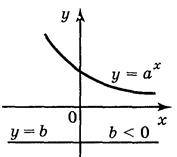
Рис. 152
Рис. 153
Для того щоб розв’язати рівняння aх = b, де а > 0, а? 1, b > 0, треба b подати у вигляді b = аc, тоді будемо мати аx = ac, звідси х = с.
Розглянемо Розв’яжіть приклади.
Приклад 1. рівняння 5х = 125.
Оскільки 5х = 125, а 125 = 53, то маємо 5х = 53, звідси х = 3.
Відповідь: 3.
Приклад 2. Розв’яжіть рівняння 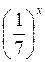 = 49.
= 49.
Оскільки 49 = 72 = 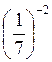 , то
, то 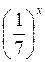 =
= 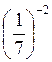 , звідси х = – 2.
, звідси х = – 2.
Відповідь: -2.
Приклад 3. Розв’яжіть рівняння 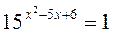 .
.
Оскільки 1 = 150, то 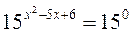 , х2 – 5х + 6 = 0, звідси х1 = 2, х2 = 3.
, х2 – 5х + 6 = 0, звідси х1 = 2, х2 = 3.
Відповідь: 2; 3.
Приклад 4. Розв’яжіть рівняння 2 х – 2 = -2.
Оскільки 2 х – 2 > 0 при всіх значеннях х, то рівняння коренів не має.
Відповідь: немає коренів.
III. Набуття умінь у розв’язуванні простіших показникових рівнянь
1. Які з чисел 0; 1; 2 є коренями рівняння 5х + 2 = 125?
Відповідь: 1.
2. Розв’яжіть рівняння: а) 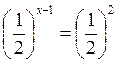 ; б)
; б) 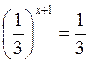 ; в) 52х – 1 = 53; г) 7х – 2 = 73;
; в) 52х – 1 = 53; г) 7х – 2 = 73;
Відповідь: a) 3; 6) 0; в) 2; г) 5.
3. Розв’яжіть рівняння: а) 2х = 32; б) 10х = 1000; в) 3х = 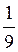 ; г) 5х =
; г) 5х = 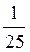 ; д) 13х = 1.
; д) 13х = 1.
Відповідь: а) 5; б) 3; в) -2; г) -2; д) 0.
1. Розв’язати рівняння: а) 2 х – 1 = 4; б) 0,5 2х – 1 = 0,125; в) 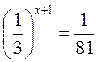 ; г) 27х =
; г) 27х = 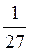 .
.
Відповідь: а) 3; б) 2; в) 3; г) -1.
2. Розв’яжіть рівняння: а) 2х – 2 = 0; б) 3х – 1 = 0; в) 5х – 1 – 1 = 0; г) 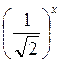 +1 = 0.
+1 = 0.
Відповіді: а) 1; б) 0; в) 1; г) коренів немає.
3. Розв’яжіть рівняння: а) 3х – 3 = 81; б) 2 – 2х = 32; в) 5 – 3х = 15; г) 7 – 2х = 28.
Відповідь: а) 3; б) 4; в) 1; г) 2.
Достатній рівень
1. Розв’яжіть рівняння: а) 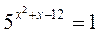 ; б)
; б) 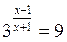 ; в)
; в) 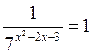 ; г)
; г) 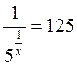 .
.
Відповідь: а) -4; 3; б)-3; в) 3;-1; г) 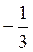 .
.
2. Розв’яжіть рівняння:
А) 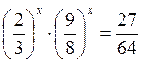 ; б)
; б) 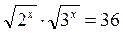 ; в)
; в)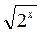 = 4; г)
= 4; г) 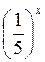 :2х = 0,01.
:2х = 0,01.
Відповідь: а) 3; б) 4; в) 4; г) 2.
3. Розв’яжіть рівняння: а) 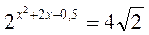 ; б)
; б) 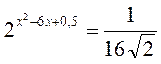 .
.
Відповідь: а) -3; 1; б) 1; 5.
Високий рівень
1. Розв’яжіть рівняння:
А) 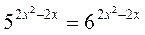 ; б)
; б) 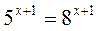 ; в)
; в) 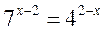 ; г)
; г) 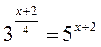 .
.
Відповідь: а) 0; 1; б) -1; в) 2; г) -2.
2. Розв’яжіть рівняння: а) 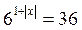 ; б)
; б) 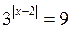 .
.
Відповідь: а) -1; 1; б) 0; 4.
3. Розв’яжіть рівняння: а) 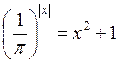 ; б)
; б) 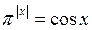 .
.
Відповідь: а) 0; б) 0.
IV. Підсумок уроку
V. Домашнє завдання
Розділ IV § 2 стор. 214-216. № 29, 30 з “Запитання і завдання для повторення”. № 1 (1-10).
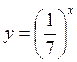 ;
; 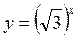 ;
; 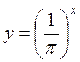 є
є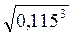 і
і 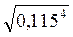 ;
;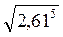 і
і 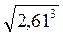 ;
;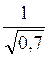 i
i 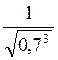 .
.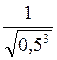 і
і 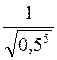 .
.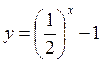 .
.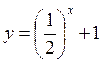
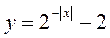 .
.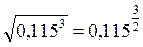 ;
; 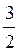 < 2 , то
< 2 , то 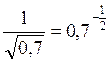 ,
, 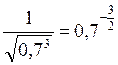 .
. > –
> – 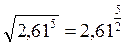 ,
, 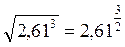 .
.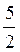 >
> 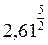 >
> 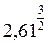 , отже
, отже 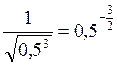 ,
, 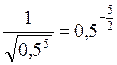 .
.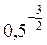 <
< 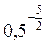 , отже
, отже 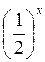 > 0, то
> 0, то