Рівняння прямої
Геометрія
Декартові координати на площині
Рівняння прямої
Будь-яка пряма в декартових координатах x, y має рівняння виду:
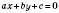 , де a, b, c – деякі числа.
, де a, b, c – деякі числа.
Знаходження координат точки перетину прямих та випадки розміщення прямої відносно системи координат описано в розділі “Алгебра. 8 клас” (“Лінійна функція”).
Рівняння прямої, яка перетинає осі координат в точках 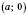 і
і 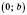 , де
, де 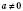 ,
, 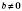 , можна
, можна
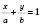 .
.Кутовий коефіцієнт у рівнянні прямої
Якщо рівняння прямої можна записати у вигляді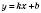 , то коефіцієнт k називається Кутовим коефіцієнтом прямої.
, то коефіцієнт k називається Кутовим коефіцієнтом прямої.
1. Дві прямі паралельні тоді й тільки тоді, коли у них збігаються кутові коефіцієнти, а точки перетину з віссю ординат різні.
2. Кутовий коефіцієнт з точністю до знака дорівнює тангенсу гострого кута, утвореного прямою з віссю абсцис (або дорівнює тангенсу кута між прямою й додатним напрямком осі Ox).
3. Прямі, що задані рівняннями 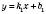 і
і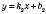 , перпендикулярні тоді й тільки тоді, коли
, перпендикулярні тоді й тільки тоді, коли 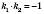 .
.




 (1 votes, average: 5.00 out of 5)
(1 votes, average: 5.00 out of 5)Related posts:
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...
- Рівняння прямої УРОК № 28 Тема. Рівняння прямої Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...
- Рівняння сфери, площини і прямої 79. (x – 1)2 + у2 + (2 – 4)2 = 25. 80. A(10; 0; 0), В(0; 10; 0), С(0; 0; 10). 81. M(3; 2; -1) не належить сфері. X2+ у2 + z2 – 2х + 4у – 6z – 2 = 0, бо 32 + 22 + (-1)2 – 2 × 3 + 4 […]...
- Рівняння з двома змінними 909. Рівняннями з двома змінними є рівняння; 1), 3), 5), 6), 8), 9). 910. 1) 4x + 3y = 1; 4 • (-2) + 3 • 3 = 1 – правильна рівність, тому (-2; 3) – розв’язок даного рівняння. 2) x2 + 5 = у2; (-2)2 + 5 = 32 – правильна рівність, тому (-2; […]...
- Взаємне розміщення кола і прямої – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Взаємне розміщення кола і прямої Коло і пряма не мають спільних точок. Коло і пряма мають одну спільну точку. А – дотична А – точка дотику Коло і пряма мають дві спільні точки. А – січна Рівняння кола (х – а)2 + (y – b)2 = R2, де (а, b) […]...
- Симетрія відносно прямої УРОК № 35 Тема. Симетрія відносно прямої Мета уроку: формування поняття симетрії відносно прямої; вивчення властивостей симетрії відносно прямої; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують симетрію відносно прямої; будує фігури, у які переходять дані […]...
- Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...
- Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...
- Перпендикуляр до прямої Урок № 19 Тема. Перпендикуляр до прямої Мета: домогтися розуміння учнями змісту теореми про існування та єдиність прямої, що проходить через будь-яку точку площини перпендикулярної даній; понять: “перпендикуляр, проведений з точки до прямої”, “відстані від точки до прямої”. Сформувати вміння: – відтворювати зміст зазначеної теореми та застосовувати її під час розв’язування задач; – на рисунку […]...
- Системи рівнянь – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Лінійне рівняння з однією змінною – рівняння, що зводиться до канонічного вигляду ах + b = 0, де х – змінна, а й b – константи. Корінь рівняння ах + b = 0 визначається формулою: х = – b/а – якщо а ≠ 0, множина розв’язків L = {-b/a}. – […]...
- Відстань від точки до прямої. Розв’язування задач на застосування теореми про три перпендикуляри Урок 35 Тема. Відстань від точки до прямої. Розв’язування задач на застосування теореми про три перпендикуляри Мета уроку: формування вмінь учнів застосувати теорему про три перпендикуляри до розв’язування задач, знаходження відстані від точки до прямої. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання. 1. Два учні відтворюють на дошці розв’язування задач № 13, 41. […]...
- Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Урок 13 Тема. Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Мета уроку: формування знань учнів про взаємне розміщення прямої і площини в просторі. Вивчення ознаки паралельності прямої і площини. Обладнання: стереометричний набір, моделі куба і тетраедра, схема “Аксіоми стереометрії”. Хід уроку І. Аналіз виконання тематичного оцінювання № 1. Зібрати зошити наприкінці […]...
- Графік лінійного рівняння з двома змінними Розв’яжіть задачі. 1078. мал. 74. Графіком лінійного рівняння з двома змінними є пряма. 1079. 1) с = 0; 2) а = 0; 3) b = 0; 4) а = 0; с = 0; 5) b = 0; с = 0. 1080. 1) -6 – 2 • 2,5 + 1 ≠ 0; -5 – 5 ≠ […]...
- Перетин прямої з площиною. Перерізи многогранників УРОК 3 Тема. Перетин прямої з площиною. Перерізи многогранників Мета уроку: ознайомлення учнів із взаємним розташуванням прямої і площини у просторі. Вивчення теореми про належність прямої до площини. Формування поняття перерізу многогранника. Обладнання: моделі многогранників, схема “Взаємне розташування прямої і площини”, стереометричний набір. 1. Фронтальне опитування. 1) Скільки площин визначають дві прямі, які перетинаються? 2) […]...
- Властивості прямої і площини, перпендикулярних між собою Урок 30 Тема. Властивості прямої і площини, перпендикулярних між собою Мета уроку: формування знань учнів про властивості перпендикулярних прямих і площин. Обладнання: стереометричний набір, схема “Властивості прямо і площини, перпендикулярних між собою” (с. 116). Хід уроку І. Перевірка домашнього завдання 1. Колективне обговорення розв’язування задачі № 10. 2. Математичний диктант. Дано зображення куба: варіант 1 […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg t = a УРОК 22 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg T = a. Мета уроку: зсвоєння учнями виведення і застосування формули для знаходження коренів рівняння tg t = a (ctg t = а). Обладнання: Таблиця “Рівняння tg t = а і ctg t = a”. І. Перевірка домашнього завдання 1. Перевірити наявність домашніх завдань в зошитах […]...
- Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...
- Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини Урок 27 Тема. Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини Мета уроку: формування поняття прямої, перпендикулярної до площини. Вивчення ознаки перпендикулярності прямої і площини. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Відповіді на запитання, які виникли в учнів при виконанні домашнього завдання. 2. Самостійна робота. Варіант 1 1) Промені OВ, ОС, OD […]...
- Лінійне рівняння з двома змінними та його графік Урок № 70 Тема. Лінійне рівняння з двома змінними та його графік Мета: формувати свідоме розуміння означення лінійного рівняння з двома змінними та вигляду графіка лінійного рівняння з двома змінними (зокрема, його особливих видів); виробляти вміння: відрізняти лінійне рівняння з двома змінними з-поміж інших рівнянь; будувати графіки лінійних рівнянь із двома змінними; подальше вдосконалювати вміння […]...
- Теорема про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій Урок 8 Тема. Теорема про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій Мета уроку: вивчення теореми про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Фронтальне опитування. 1) Які прямі в просторі називаються паралельними? 2) Вкажіть […]...
- Розв’язування задач на застосування ознаки перпендикулярності прямої і площини Урок 28 Тема. Розв’язування задач на застосування ознаки перпендикулярності прямої і площини Мета уроку: формування вмінь учнів застосовувати означення та ознаку перпендикулярності прямої і площини до розв’язування задач. Обладнання: стереометричний набір, модель куба. Хід уроку І. Перевірка домашнього завдання 1. Перевірка правильності розв’язання задачі № 7 за записами (з пропусками), зробленими на дошці до початку […]...
- Координатна площина Математика – Алгебра Раціональні числа Координатна площина Проведемо дві перпендикулярні координатні прямі, які перетинаються в початку їх відліку – точці О. Ці прямі називаються Осями координат. Горизонтальну пряму називають Віссю абсцис І позначають Ox, вертикальну – Віссю ординат І позначають Oy. Точку О називають Початком координат. Ці координатні прямі утворюють Декартову прямокутну систему координат. Площина, […]...
- Означення квадратного рівняння. Неповні квадратні рівняння та їх розв’язування Урок № 48 Тема. Означення квадратного рівняння. Неповні квадратні рівняння та їх розв’язування Мета: закріпити знання учнів щодо означення квадратного рівняння, коефіцієнтів квадратного рівняння та його видів; домогтися засвоєння учнями способів розв’язання неповних квадратних рівнянь; сформувати вміння застосовувати вивчений матеріал для розв’язування неповних квадратних рівнянь. Тип уроку: засвоєння знань та вмінь. Наочність та обладнання: опорний […]...
- ІДЕАЛЬНИЙ ГАЗ. ОСНОВНЕ РІВНЯННЯ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ ІДЕАЛЬНОГО ГАЗУ (РІВНЯННЯ КЛАУЗІУСА) Фізика підготовка до ЗНО комплексне видання МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА 1. ОСНОВИ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ 1.5. ІДЕАЛЬНИЙ ГАЗ. ОСНОВНЕ РІВНЯННЯ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ ІДЕАЛЬНОГО ГАЗУ (РІВНЯННЯ КЛАУЗІУСА) Ідеальний газ – де газ, у якому середня відстань між молекулами набагато більша від розмірів молекул, і тому в ньому потенціальною енергією молекул нехтують (рис. 3). Рис. З Середня квадратична […]...
- ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &22. ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ Ви знаєте, що кожній упорядкованій парі чисел відповідає певна точка на координатній площині. Оскільки кожний розв’язок рівняння з двома змінними х і у – це упорядкована пара чисел, то всі його розв’язки можна зобразити точками па координатній площині. У цих точок […]...
- Поворот і симетрія відносно прямої 373. Із т. А опустимо перпендикуляр AD + l. Відкладемо ∠ΑΟΛ, = α, А1O + l. Виконано поворот т. А навколо прямої l на кут α. Аналогічно вчинимо з т. В. Відрізок АВ у результаті повороту на кут α навколо прямої l відобразиться у відрізок. 374. Таких поворотів безліч. 375. Точка А(1; 2; 0) відобразиться […]...
- Рівняння. Кути. Прямокутник. Трикутник і його види УРОК 41 Тема. Рівняння. Кути. Прямокутник. Трикутник і його види Мета: підготовити учнів до тематичної контрольної роботи. Тип уроку: повторення і систематизація знань. Хід уроку I. Актуалізація опорних знань Усні вправи 1. Знайти корінь рівняння: 1) х + 15 = 29; 2) 30 – х = 17; 3) х – 12 = 19; 4) 12 […]...
- Перпендикуляр Геометрія Основні властивості найпростіших геометричних фігур Перпендикуляр Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом (див. рисунок), тобто, коли вони перетинаються, утворюються чотири прямих кути. Позначення: . Теорема 1. Через кожну точку прямої можна провести перпендикулярну до неї пряму, і до того ж тільки одну. Перпендикуляром до даної прямої називається відрізок прямої, перпендикулярної […]...
- Перетворення подібності та його властивості. Гомотетія УРОК № 38 Тема. Перетворення подібності та його властивості. Гомотетія Мета уроку: формування понять перетворення подібності й гомотетії; вивчення властивостей перетворення подібності; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення подібності” [13]. Вимоги до рівня підготовки учнів: описують перетворення подібності й гомотетію; будують фігури, у […]...
- Рівняння. Кути. Трикутники УРОК 42 Тема. Рівняння. Кути. Трикутники Мета: перевірити рівень засвоєння учнями навчального матеріалу; перевірити рівень сформованості вмінь учнів: вимірювати і будувати кути за допомогою транспортира; обчислювати невідомі сторони й периметр трикутника; розв’язувати рівняння з використанням правил знаходження невідомих компонентів дій додавання і, віднімання. Тип уроку: контроль знань. Хід уроку І. Тематична контрольна робота № 3 […]...
- Точка та прямі § 1. Найпростіші геометричні фігури та їхні властивості 1. Точка та прямі Практичні завдання 1. 2. Прямі ME, МК, ЕК, EM, КМ, КЕ. 3. Точка С належить прямій а, точка С належить прямій b. 4. Утворилося три прямих. 5. 6. Можна отримати три або одну точку перетину. 7. 1) 2) 3) Вправи 8. 1) Прямій […]...
- Графік лінійного рівняння із двома змінними 894. (0; 1); (-1; 0); (2; 3). 895. 2х – у = 1. А) A(1; 1) – належить графіку даного рівняння, бо 2 • 1 – 1 = 1 – правильна рівність; Б) В(2; 1) – не належить графіку даного рівняння, бо 2 • 2 – 1 = 1 – неправильна рівність; В) С(0; 1) […]...
- Описані і вписані кола Розділ 1. Найпростіші геометричні фігури та їх властивості § 17. Описані і вписані кола 671. Коло, описане навколо трикутника, зображено на мал. 372. 672. Коло, вписане у трикутник, зображено на мал. 375. 673. Центр кола, описаного навколо гострокутного трикутника, лежить всередині трикутника. Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи. Центр кола, описаного […]...
- Підсумковий урок з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Урок № 54 Тема. Підсумковий урок з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Мета: повторити, систематизувати та узагальнити знання і вміння учнів щодо виділення квадратних рівнянь серед інших рівнянь з однією змінною, класифікації квадратних рівнянь, а також застосування різних (передбачених програмою з математики) способів розв’язання квадратних рівнянь різного виду. Тип уроку: систематизація […]...
- Тематична контрольна робота з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Урок № 55 Тема. Тематична контрольна робота з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Мета: перевірити рівень засвоєння учнями змісту основних понять теми “Квадратні рівняння” та рівень умінь, сформованих у ході вивчення теми. Тип уроку: контроль знань та вмінь. Хід уроку I. Організаційний етап II. Перевірка домашнього завдання Зібрати зошити із виконаною […]...
- Розв’язання систем лінійних рівнянь способом підстановки Рівень А Відповідь: (1; 3). Відповідь: (7; -4,5). Відповідь: (1; 3). Відповідь: (4; 1). Відповідь: (3; 1). Відповідь: (1;-2). Відповідь: розв’язків немає. Відповідь: (3; 2). Відповідь: (4; 0). Відповідь: (3; 5). Відповідь: (1,5; 2). Відповідь: (3; -1). Відповідь: (7; 1). Відповідь: (1; -1). Рівень Б Відповідь: (2; 1,5). Відповідь: (1; -2). Відповідь: (20; 0,5). Відповідь: […]...
- Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...
- Лінійні рівняння з однією змінною 793. Лінійними рівняннями є рівняння: а) 2/9х = 8; в) -2,7y = 0. 794. а) 56х = 64; рівняння має 1 корінь, Б) 0х = -2; рівняння не має коренів; В) 8х = 0; рівняння має 1 корінь, х = 0; Г) 0у = 0; рівняння має безліч коренів. 795. а) 6х = 42; х […]...
- Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k і b – дані числа. Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до […]...
- ПЕРПЕНДИКУЛЯРНІ І ПАРАЛЕЛЬНІ ПРЯМІ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 5. ПЕРПЕНДИКУЛЯРНІ І ПАРАЛЕЛЬНІ ПРЯМІ Пригадайте, як можуть розташовуватися на площині дві прямі. Якщо вони перетинаються, то утворюють чотири кути – дві пари вертикальних кутів. Йдеться про кути, менші від розгорнутого. Менший із цих кутів вважають кутом між даними прямими. Наприклад, на малюнку 56 прямі АВ і […]...