Рівняння сфери, площини і прямої
79.
(x – 1)2 + у2 + (2 – 4)2 = 25.
80.
A(10; 0; 0), В(0; 10; 0), С(0; 0; 10).
81.
M(3; 2; -1) не належить сфері.
X2+ у2 + z2 – 2х + 4у – 6z – 2 = 0, бо
32 + 22 + (-1)2 – 2 × 3 + 4 × 2 – 6 × (-2) – 2 = 0 – невірно.
Тобто координати точки М не задовольняють рівнянню сфери.
82.
R2 = ВМ2 = (2 – 1)2 + (0 – 1)2 + (-1 – 3)2 = 1 + 1 + 16 = 18.
Тоді рівняння сфери має вигляд: (x – 1)2 + (у – 1)2 + (z – 3)2 = 18.
83.
АВ – діаметр, О – центр сфери – середина АВ.
0(-1; 2; 3); R2 = ОA2 = (-2 + 1)2 + (1 – 2)2 + (4 – 3)2 = 1 + 1 + 1 = 3.
Тоді рівняння сфери має вигляд: (х + 1)2 + (у – 2)2 +
84.
R2 = АВ2 – (0 + 2)2 + (2 – 1)2 + (1 – 3)2 = 4 + 1 + 4 = 9.
Рівняння сфери:
1) Якщо А – центр сфери: (х + 2)2 + (у – 1)2 + (z – 3)2 = 9.
2) Якщо В – центр сфери: x2 +(y – 2)2 + (z – 1)2 = 9.
85.
Якщо сфера перетинає вісь х, то в точках перетину х = 0, у = 0
X2 + 02 + 02 – 4х = 12; х2 – 4x – 12 = 0; x = -2, х = 6.
(-2; 0; 0), (6; 0; 0) – точки перетину сфери з віссю х.
86.
Точки перетину з віссю х:
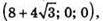
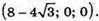
Х2 – 16x + 19 = 0;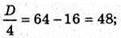 
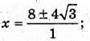
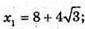
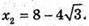
Точки перетину з віссю у: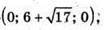 
У2 – 12у + 19 = 0;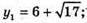 
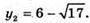
Точки перетину з віссю z: z2 + 19 = 0, рівняння розв’язків немає.
Сфера не перетинає вісь z.
87.
(х – 2)2 + (у – 4)2 + (z – З)2 = 25 – рівняння сфери.
Точки перетину сфери з площиною (ху) мають координати (х; у·, 0).
Тоді (х – 2)2 + (у – 4)2 + 32 = 25 – рівняння лінії перетину сфери і площини (ху).
(x – 2)2 + (у – 4)2 = 16 – рівняння лінії перетину.
Лінія перетину – коло з центром (2; 4; 0), R = 4.
L = 2πR = 2π × 4 = 8π.
88.
А) (-2; 3; 1) – центр. (-2; 3; 0) – точка сфери, R = 1.
(х + 2)2 + (у – 3)2 + (z – 1)2 = 1.
Б) (-2; 3; 1) – центр. (0; 3; 1) – точка сфери, R = 2.
(х + 2)2 + (у – 3)2 + (z -1)2 = 4.
В) (-2; 3; 1) – центр. (-2; 0; 1) – точка сфери, R = 3.
(х + 2)2 + (у – 3)2 + (2 – 1)2 = 9.
89.
А) х2 + у2 + 22 – 2х + 4у – 2z = 31;
(х2 – 2x + 1) + (у2 + 4у + 4) + (z2 – 2х + 1) – 6 = 31;
(х – 1)2 + (у + 2)2 + (z – 1)2 = 37;
(1; -2; 1) – центр,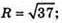 
Б) х2 + у2 + z2 + 6х – 2у = 26;
(х2 + 6х + 9) + (у2 – 2у + 1) + z2= 26 + 10;
(х + 3)2 + (у – 1)2 + z2 = 36;
(-3; 1; 0) – центр, R = 6.
90.
Площина 2x + 4у + Зz – 7 = 0 не проходить через точу А(2; 3; -1),
Бо 2 × 2 + 4 × 3 + 3 × (-1) – 7 = 0 – невірно.
Площина 2х + 4у + Зz – 7 = 0 проходить через точку B(-1; 0; 3),
Бо 2 х (-1) + 4 х 0 + 3 × 3 – 7 = 0 – вірно.
91.
Точка перетину з віссю х: (-3; 0; 0). 2 × x – 0 + 3 × 0 + 6 = 0; x = -3.
Точка перетину з віссю у: (0; 6; 0). 2 × 0 – у + 3 × 0 + 6 = 0; у = 6.
Точка перетину з віссю z: (0; 0; -2). 2 × 0 – 0 + 3 × 2 + 6 = 0; z = -2.
92.
Якщо площина проходить через вісь х, то будь-яка точка осі х лежить на площині, наприклад (0; 0; 0), (5; 0; 0) і за умовою площина проходить через А(1; 1; 1).
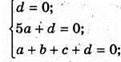
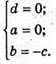
Ах + by + cz + d = 0; 0 × х – су + сz + 0 = 0 або у – z = 0 – рівняння площини, яка проходить через А(1; 1; 1) і вісь х.
93.
Якщо площина проходить через т. А(2; 3; 4) і паралельна площині (ху),
То ця площина проходить через будь-яку точку (х; у; 4), наприклад, (0; 5; 4) і (0; 0; 4).
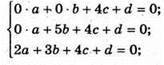
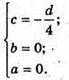
Тоді рівняння площини має вигляд:
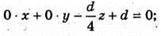
Dz – 4d = 0; z – 4 = 0; z = 4 – шукане рівняння.
94.
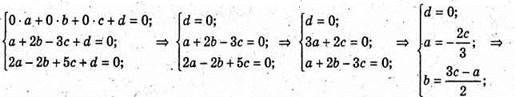
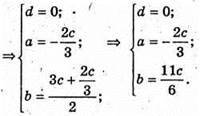
Звідси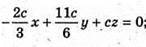 
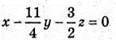або 4х – 11у – 6z = 0.
95.
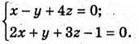
Якщо пряма перетинає площину (ху), то z = 0,
Тоді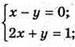 
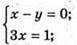
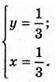
Тоді точка перетину з площиною (ху) має координати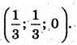 
Якщо пряма перетинає площину (хz), то у = 0.
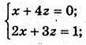
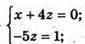
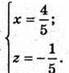
Тоді точка перетину з площиною (хz) має координати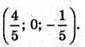 
Якщо пряма перетинає площину (уz), то х = 0.
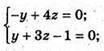
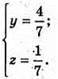
Точка перетину з площиною (уz) має координати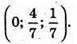 
96.
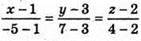або 
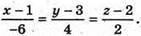
97.
(0; 5,8; -6,2), (8; 1; 5), (13; -2; 12).
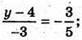y = 5,8; 
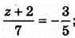z = -6,2.
98.
О – середина MN;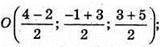 
0(1; 1; 4).
Рівняння прямої P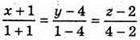О: 
або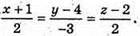 
99.
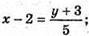5x – 10 = у + 3; у = 5х – 13;
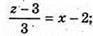z = 3x – 3.
3x – 2(5x – 13) + 3x – 3 – 7 = 0; 3x – 10x + 26 + 3x – 10 = 0;
-4x = -16; x = 4; y = 5 × 4 – 13 = 7; 2 = 3 × 4 – 3 = 9.
(4; 7; 9) – точка перетину прямої і площини.
100.
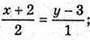x + 2 = 2у – 6; x = 2у – 8;
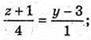z + 1 = 4y – 12; z = 4y – 13;
(2y – 8)2 + y2 + (4y – 13)2 = 13;
4y2 – 32y + 64 + y2 + 16y2 – 104y + 169 = 13; 21y2 – 13y + 220 = 0;
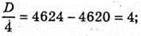
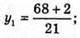
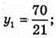
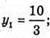
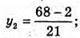
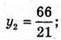
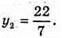
Тоді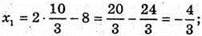 
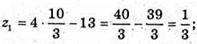
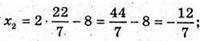
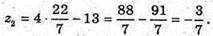
Отже, пряма і сфера перетинаються в точках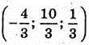 
і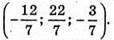 
101.
Площину (ху) сфера перетинає по колу радіуса А2О, 
Центр кола Аz(2; 3; 0), коло задається рівнянням (x – 2)2 + (у – 3)2 + z2= 13.
Площину (хz) сфера перетинає по колу з центром А (2; 0; 4),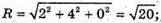 
(x – 2)2 + y2 + (z – 4)2 = 20.
Площину (zy) сфера перетинає по колу з центром (0; 3; 4),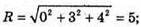 
X2 + (у – 3)2 + (z – 4)2 = 25.
102.
Нехай (x; у; z) – центр кола. Тоді R2 = (x – 4)2 + (y – 4)2 + (z – 2)2;
R2 = x2 + у2 + (z – 2)2; R2 = x2 + (у – 4)2 + z2; R2 = x2 + y2 + х2.
Маємо систему: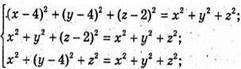 
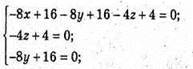
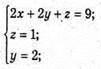
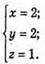R2 = x2 + у2 + z2 = 22 + 22 +12 = 9, (2; 2; 1) – центр кола.
Рівняння має вигляд: (x – 2)2 + (у – 2)2 + (z – 1)2 = 9.
103.
Оскільки центр лежить на осі z, то центр має координати (0; 0; z).
Тоді R = ОА = 0B, звідки ОА2 = ОВ2.
ОА2 = 52 + (1 – z)2; ОB2 = (-2)2 + (4 – z)2; ОА2 = ОB2.
52 + (1 – z)2 = 4 + (4 – z)2; 25 + 1 – 2z + z2 = 4 + 16 – 8z + z2;
6z = -6; z = -1; (0; 0; -1) – центр кола,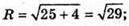 
R2 = 29.
Рівняння має вигляд х2 + у2 + (z + 1)2 = 29.
104.
ГМТ є сфера з центром (2; 1; -4) і R = 7 або R = 3.
105.
Х2 + у2 + z2 – 4х + 2у = 4; (x2 – 4x + 4) + (у2 + 2y + 1) + z2= 4 + 5;
(х – 2)2 + (у + 1)2 + z2= 9 – сфера з центром O(2; -1; 0), R = 3.
(х – 6)2 + (y + 1)2 + (z – З)2 = а2 – сфера з центром O1(6; -1; 3), R = а.
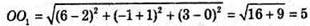– відстань між центрами.
Якщо а = 5 – 3 = 2 або а = 5 + 3 = 8, то сфери мають одну спільну точку
(дотикаються зовнішнім та внутрішнім дотиком).
Якщо а? (2; 8), то сфери перетинаються. Якщо а? (0; 2)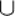 
(8; +∞), то сфери спільних точок не мають.
106.
А)
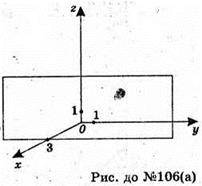
Х = 3 – площина, яка проходить через т. (3; 0; 0) і паралельна площині (уz);
Б)
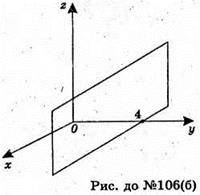
Площина у = 4 проходить через т. (0; 4; 0) паралельно площині (xz);
В)
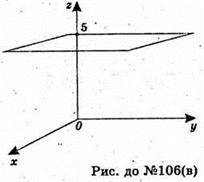
Z = 5 – площина, яка проходить через т. (0; 0; 5) паралельно площині (ху);
Г)
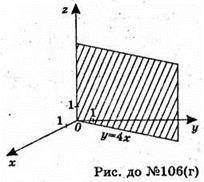
У – 4х = 0 – площина, яка проходить через пряму у – 4х і вісь z;
Г)
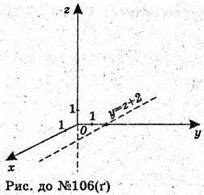
У – z – 2 = 0 – площина, яка проходить через пряму у = z + 2
Перпендикулярно до площини (zу);
Д)
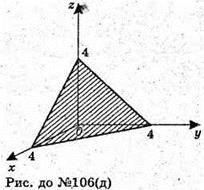
Х + у + z = 4 – площина, яка проходить через точки (4; 0; 0); (0; 4; 0); (0; 0; 4).
107.
Ах + by + сz = 0 – рівняння площини, яка проходить через початок координат
(0; 0; 0), оскільки за будь-яких значень а, b, с координати точки
(0; 0; 0) задовольняють рівнянню.
А × 0 + b × 0 + с × 0 = 0 – вірно.
108.
А(а; b; с) – точка площини, основа перпендикуляра ОА.
Р(х; у; z) – довільна точка площини.
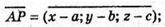
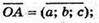
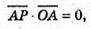бо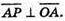 
А(х – а) + b(у – b) + с(z – с) = 0; ах – а2 + by – b2 + сz – с2 = 0;
Ах + by + сz – (а2 + b2 + с2) = 0- рівняння площини а.
109.
Складемо рівняння площини, яка проходить через т. A(2; 0; 0);
Т. B(0; 2; 0) і т. С(0; 0; 2).
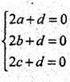
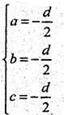
Ax + by + cz + d = 0
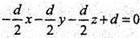або x + y + z – 2 = 0.
110.
A(a; 0; 0); т. B(0; b; 0) і т. C(0; 0; c). Ax + By + Cz + D = 0
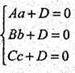
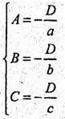
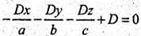або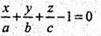 
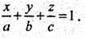
111.
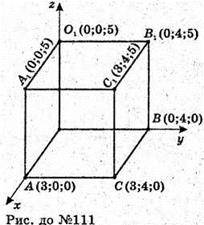
A(4; 0; 0); т. B(0; 4; 0) і т. C(3; 4; 0).
Площина AОВ: z = 0.
Площина AOO1: у = 0.
Площина BOO1: x = 0.
Площина ACC1: x = 3.
Площина СВВ1: у = 4.
Площина А1С1В1: z = 5.
112.
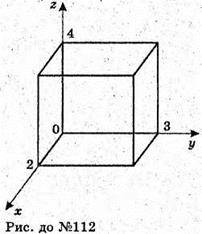
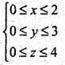
Координати точок прямокутного паралелепіпеда задовольняють
Систему нерівностей.
113.
4х + 3у – 4 = 0 – рівняння площини. x2 + у2 + z2 – 2х + 8у + 8 = 0;
(x2 – 2х + 1) + (у2 + 8у +16) + z2- 17 + 8 = 0;
(x – 1)2 + (у + 4)2 + z2 = 9 – рівняння сфери.
O(1; -4; 0) – центр сфери. Якщо т. О належить даній площині,
То координати точки О задовольняють рівнянню сфери.
Перевіримо: 4 × 1 + 3 × (-4) – 4 = 0 – невірно, тому центр сфери
Не лежить в даній площині.
114.
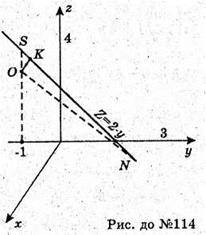
O(0; -1 ; 2) – центр сфери, знаходиться у площині (уz).
Площина z = 2 – у перетинає площину (zу) по прямій z = 2 – у, а сферу перетне по колу, радіус якого г ми знайдемо з ΔOKN, де ON – радіус R сфери; ОK – відстань від т. О до прямої z = 2 – у.
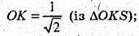
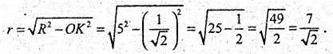
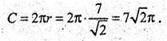
115.
Знайдемо Р – точку перетину відрізка АВ і площини Зх + 2y + z – 17 = 9.
Рівняння АВ: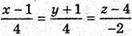 
або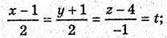 
х = 2t + 1; у = 2t – 1; z = – t + 4.
Підставимо в рівняння площини: 3 × (2t + 1) + 2(2t – 1) – t + 4 – 17 = 0;
6t + 3 + 4t – 2 – t – 13 = 0; 9t = 12;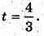 
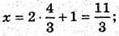
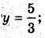
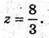
Отже,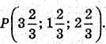 
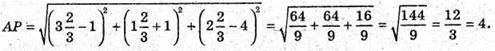
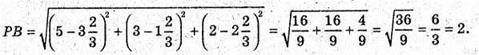
Р – точка перетину відрізка і площини ділить відрізок АВ у відношенні 
(1 votes, average: 5.00 out of 5)
Loading...