Розв’язування логарифмічних рівнянь
УРОК 58
Тема. Розв’язування логарифмічних рівнянь
Мета уроку. формування умінь учнів розв’язувати логарифмічні рівняння різними методами: зведення логарифмічного рівняння до алгебраїчного; метод потенціювання; зведення логарифмів до однієї і тієї самої основи; метод логарифмування та графічний метод.
І. Перевірка домашнього завдання
1. Усне розв’язування логарифмічних рівнянь з використанням таблиці 24 для усних обчислень “Логарифмічні рівняння”.
1 | 2 | 3 | 4 | 5 | |
1 | Log5 |
| Log9 x = | Log7x = 1 | Log3 x = -2 |
2 | Log2(-x) = -3 | Log5(x – 2) = 2 |
| Lg(x + 3) = lg x | Lg(x+1) = lg(x+1) |
3 | Lg(2x+1) = lg x | Lg x2 = 0 | Log2(x – 4) = 3 | Log3(x – 1) = 0 | Log3(x – 1) = 1 |
4 | Lg(x – 3) = -2 | Lg(5 – x) = – 1 | Lg | Lg | Lg cos x = 1 |
5 | Log x+1 2 = 1 | Logx 5 = | Lg sin x = 0 | Lg lg x = 0 | Lg lg x = 1 |
2. Обговорення запитань, що виникли під час виконання домашніх завдань.
II. Сприймання і усвідомлення різних методів розв’язування логарифмічних рівнянь
1. Метод зведення логарифмічного рівняння до алгебраїчного.
Приклад. Розв’яжіть рівняння log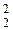
х – 3log2 x = 4.
Розв’язання
Позначимо log2 x через у. Дане рівняння набере вигляду:
У2 – 3y = 4; у2 – 3у – 4 = 0; у1 = 4; у2 = -1.
Звідси log2 x = 4, log2 x =-1;
X = 24; x = 2-1; x = 16, x = 
.
Перевірка: 1) log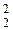 16 – 3 log2 16 = 16 – 12 = 4;
2) log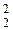 – 3 log2 = -1 + 3 = 4.
Відповідь: 16; .
2. Метод потенціювання.
Приклад. Розв’яжіть рівняння log5(x – 1) + log5(x – 2) = log5(x + 2).
Розв’язання
Пропотенціюємо дану рівність і одержимо:
Log5((x – 1)(х – 2)) = log5(x + 2); (х – 1)(х – 2) = х + 2; x2 – 2х – х + 2 = х + 2;
X2 – 4х = 0; х(х – 4) = 0; х = 0 або х = 4.
Перевірка:
1) Значення х = 0 не є коренем рівняння, тому що вирази log5(x – 1) і log5(x – 2) не мають смислу при х = 0.
2) log5(x-1) + log5(x-2) = log5(4-1) + log5(4-2) = log53 + log52 = log5(2-3) = log56.
Log5(x + 2) = log5(4 + 2) = log56.
Отже, х = 4 – корінь.
Відповідь: 4.
3. Метод зведення логарифмів до однієї і тієї ж основи.
Приклад. Розв’яжіть рівняння log3 х – 2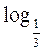
Х = 3.
Розв’язання
Log3 x – 2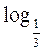X = 3; log3 х – 2 – 
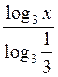= 3; log3 x – 2- 
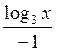= 3; log3 x + 2log3 x = 3;
3log3 x = 3; log3 x = 1; x = 3.
Перевірка: log3 3 – 2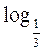3 = 1 + 2 = 3. Отже, х = 3 – корінь.
Відповідь: 3.
4. Метод логарифмування.
Приклад. Розв’яжіть рівняння х lgx = 100х.
Розв’язання
Прологарифмуємо обидві частини рівності (х > 0), одержимо:
Lgx lgx = lg(100x); lgx lgx = lg 100 + lgx; lg2x – lg x – 2 = 0.
Замінимо lg х = у. Рівняння прийме вигляд: у2 – у – 2 = 0; y1 = 2, y2 = -1.
Тоді: 1) lg х = 2; х = 102; х = 100.
2) lg x = -1; x = 10-1; x = 0,1.
Перевірка: 1) xlgx = 100 lg100 = 1002 ; 100х = 100 – 100 = 1002.
Отже, x = 100 – корінь.
2) xlgx = 0,1lg0,1 = 0,1-1 =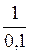 
= 10; 100х = 100 – 0,1 = 10.
Отже, x = 0,1 – корінь.
Відповідь: 100; 0,1.
5. Графічний метод розв’язування логарифмічних рівнянь.
Приклад. Розв’яжіть рівняння lg x = 1 – х графічно.
Розв’язання
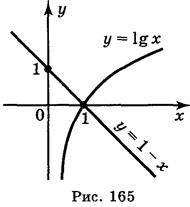
В одній і тій самій системі координат будуємо графіки функції у = lg x і у = 1 – х (рис. 165). Абсциса точки перетину побудованих графіків дорівнює 1. Отже, х = 1 – корінь даного рівняння.
Відповідь: 1.
III. Набуття умінь розв’язувати логарифмічні рівняння
Розв’язування вправ 52 (10; 14), 53 (4; 10), 54 (3; 9).
IV. Підведення підсумків уроку
V. Домашнє завдання
Розділ V § 3. Запитання і завдання для повторення розділу V № 26-31. Вправи №№ 52 (9; 11), 53 (12), 54 (2; 7).
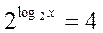
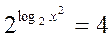
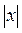(1 votes, average: 5.00 out of 5)
Loading...