Розв’язування тригонометричних рівнянь, систем та нерівностей
УРОК 31
Тема. Розв’язування тригонометричних рівнянь, систем та нерівностей
Мета уроку. Систематизувати навички і уміння розв’язувати тригонометричні рівняння, нерівності, системи.
І. Перевірка домашнього завдання
1. Три учні відтворюють розв’язування нерівностей із домашнього завдання.
2. Колективне розв’язування нерівностей:
A) sin 2x sin x – cos 2x cos х 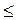
 .
.
Sin 2x sin x – cos 2x cos x 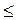
 .
.
– (cos 2x cos x – sin 2x sin x) 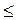
 ;
;– cos (2х – x) 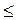
 ; cos x
; cos x 
 .
.
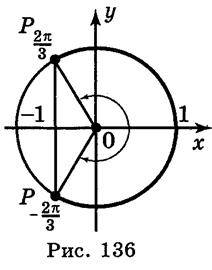
Тоді (рис. 136) – 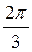 + 2?n
+ 2?n 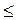 х
х 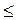
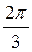 + 2?n, n
+ 2?n, n Z. Відповідь:
Z. Відповідь: 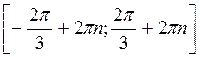 , n
, n Z.
Z.
Б)  sin x – cos x > 0.
sin x – cos x > 0.
 sin x – cos x > 0 ;
sin x – cos x > 0 ; 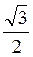 sin х –
sin х –  cos х > 0;
cos х > 0;
Sin х cos  – cos х sin
– cos х sin  > 0 ; sin
> 0 ; sin 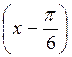
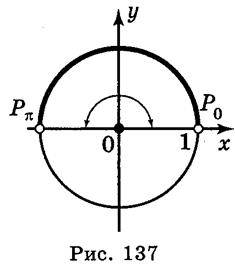
Тоді (рис. 137) 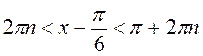 , n
, n Z;
Z;
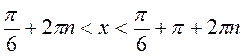 , n
, n Z;
Z;
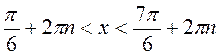 , n
, n Z.
Z.
Відповідь: 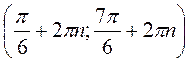 , n
, n Z.
Z.
II. Аналіз самостійної роботи, проведеної на попередньому уроці
III. Формування умінь розв’язувати тригонометричні рівняння, нерівності, системи
1. Розв’яжіть рівняння:
А) sin2 2х + sin2 4х = 1;
Б) 10 sin2 x – 12 sin x cos x – 11 cos2 x = 1;
В) cos2 x – cos 2х = 2 – sin x;
Г) 2 sin 3x + 2 cos 3х =  .
.
Відповідь: а)  +
+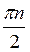 ,
, 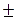
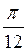 +
+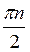 , n
, n Z;
Z;
Б) arctg 2 + ?n, – arctg 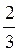 + ?n, n
+ ?n, n Z;
Z;
В)  + 2?n, n
+ 2?n, n Z; г) ±
Z; г) ±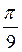 +
+ 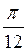 +
+ 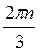 , n
, n Z.
Z.
2. Розв’яжіть системи рівнянь:
А) 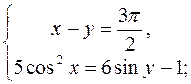 б)
б) 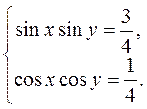
Відповідь: a) 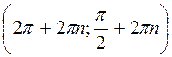 ,
, 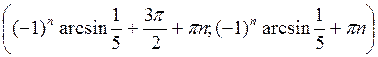 , n
, n Z;
Z;
Б) 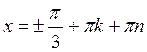 ,
, 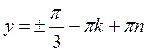 , k
, k Z, n
Z, n Z.
Z.
3. Розв’яжіть нерівності:
A) cos2 x – 2 cos x > 0;
Б) 2tg2 2х – 1 > 0.
Відповідь: а) 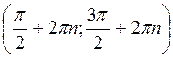 , n
, n Z;
Z;
Б) 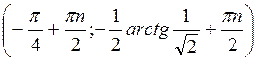 ,
, 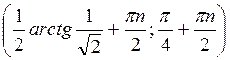 , n
, n Z.
Z.
IV. Підведення підсумків уроку
V. Домашнє завдання
Підготуватися до тематичної контрольної роботи.
Виконати вправу № 2 (24, 27, 41).
Related posts:
- Розв’язування систем тригонометричних рівнянь УРОК 27 Тема. Розв’язування систем тригонометричних рівнянь Мета уроку: познайомити учнів з окремими прийомами розв’язування систем тригонометричних рівнянь. І. Перевірка домашнього завдання 1. Чотири учні відтворюють розв’язування домашніх завдань: вправа № 2 (10; 18; 26; 38). 2. Усне розв’язування тригонометричних рівнянь, використовуючи таблицю “Тригонометричні рівняння”. 1 2 3 4 1 Sin x = 0 Cos […]...
- Розв’язування показникових рівнянь, систем і нерівностей УРОК 51 Тема. Розв’язування показникових рівнянь, систем і нерівностей Мета уроку. Формування умінь розв’язувати показникові рівняння, системи і нерівності. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування вправи № 2 (11; 13; 16). 2. Колективне розв’язування нерівностей, аналогічних домашнім: вправи № 2 (30; 31). II. Аналіз самостійної роботи, проведеної на попередньому уроці III. Формування […]...
- Розв’язування однорідних тригонометричних рівнянь УРОК 25 Тема. Розв’язування однорідних тригонометричних рівнянь Мета уроку: формування умінь учнів розв’язувати однорідні тригонометричні рівняння. І. Перевірка домашнього завдання 1. Обговорення розв’язування вправи № 2 (6; 9; 11) за готовими розв’язаннями. 2. Розв’язування аналогічних вправ. А) 1 + cos x + cos 2x = 0; Б) cos4 x – sin4 x = ; В) […]...
- Розв’язування тригонометричних нерівностей УРОК 30 Тема. Розв’язування тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати тригонометричні нерівності. І. Перевірка домашнього завдання. 1. Відповіді на запитання, які виникли у учнів при виконанні домашнього завдання. 2. Фронтальна бесіда з учнями з використанням рис. 135. 1) Які дуги відповідають нерівностям: Tg t > a, tg t < a, tg t > […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg t = a УРОК 22 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg T = a. Мета уроку: зсвоєння учнями виведення і застосування формули для знаходження коренів рівняння tg t = a (ctg t = а). Обладнання: Таблиця “Рівняння tg t = а і ctg t = a”. І. Перевірка домашнього завдання 1. Перевірити наявність домашніх завдань в зошитах […]...
- Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції УРОК 23 Тема. Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції Мета уроку: формування умінь учнів розв’язувати тригонометричні рівняння способом зведення до однієї тригонометричної функції (алгебраїчний спосіб). І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли у учнів при виконанні домашніх завдань. 2. Самостійна робота. Розв’яжіть рівняння: A) cosx = . (3 бали) […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos t = a УРОК 20 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos T = a Мета уроку: засвоєння учнями виведення і застосування формули для знаходження коренів рівняння cos t = a. Обладнання: Таблиця “Рівняння cos t = a”. І. Перевірка домашнього завдання Математичний диктант Обчисліть: 1) arcsin ; 2) arcos ; 3) arctg ; 4) arcsin; 5) arccos; […]...
- Розв’язування показникових рівнянь і систем УРОК 47 Тема. Розв’язування показникових рівнянь і систем Мета уроку. Формування умінь учнів розв’язувати показникові рівняння і системи різними способами. І. Перевірка домашнього завдання. Три учні відтворюють на відкидних дошках розв’язування вправ: 1 учень – № 34 із “Запитань для повторення”; 2 учень – № 1 (12-14); 3 учень – № 1 (15, 16). У […]...
- Розв’язування показникових рівнянь і систем показникових рівнянь УРОК 48 Тема. Розв’язування показникових рівнянь і систем показникових рівнянь Мета уроку. Формування уміння розв’язувати показникові рівняння і системи показникових рівнянь. І. Перевірка домашнього завдання 1. Чотири учні відтворюють розв’язування вправи № 1 (25, 28, 30, 46). 2. Усне розв’язування показникових рівнянь за допомогою таблиці 20 для усних обчислень “Показникові рівняння” 1 2 3 4 […]...
- Розв’язування тригонометричних рівнянь способом розкладання на множники УРОК 24 Тема. Розв’язування тригонометричних рівнянь способом розкладання на множники Мета уроку: фрмування умінь учнів розв’язувати тригонометричні рівняння способом розкладання на множники. І. Перевірка домашнього завдання Перший учень пояснює розв’язування вправи № 2 (23), другий учень – вправи № 2 (30), третій – вправи № 2 (37). II. Сприймання і усвідомлення нового матеріалу Багато тригонометричних […]...
- Розв’язування систем логарифмічних рівнянь УРОК 59 Тема. Розв’язування систем логарифмічних рівнянь Мета уроку. Формування умінь учнів розв’язувати системи логарифмічних рівнянь. І. Перевірка домашнього завдання Проводиться колективне обговорення виконання домашніх вправ за записами розв’язання вправ № 52 (9; 11), 53 (12), 54 (2; 7), підготовленими до початку уроку. II. Самостійна робота Варіант 1 Розв’яжіть рівняння: А) lg(x2 – 2х) = […]...
- Розв’язування найпростіших тригонометричних нерівностей УРОК 29 Тема. Розв’язування найпростіших тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати найпростіші тригонометричні нерівності: tg t > a, tgt < a, ctg t < a, ctg t > a (tgt a, tgt a, ctg t a, ctg t a). І. Перевірка домашнього завдання 1. Відповіді на запитання, які виникли в учнів у процесі […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = a УРОК 21 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = а Мета уроку: засвоєння учнями виведення і застосування формули для коренів рівняння sin t = а. Обладнання: Таблиця “Рівняння sin t = а”. І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли при виконанні домашніх завдань. 2. Самостійна робота. Варіант 1 Розв’яжіть рівняння: […]...
- Розв’язування ірраціональних рівнянь, систем з ірраціональними рівняннями УРОК 38 Тема. Розв’язування ірраціональних рівнянь, систем з ірраціональними рівняннями Мета уроку. Формування умінь розв’язувати ірраціональні рівняння, системи з ірраціональними рівняннями. І. Перевірка домашнього завдання 1. Відповіді на запитання учнів, що виникли в процесі виконання домашніх завдань. 2. Фронтальна бесіда за питаннями № 49-53 із “Запитання і завдання для повторення” до розділу III. 3. Усне […]...
- СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ. ГРАФІЧНИЙ СПОСІБ РОЗВ’ЯЗАННЯ СИСТЕМ Цілі: – навчальна: сформувати поняття системи двох лінійних рівнянь з двома змінними, розв’язку системи двох лінійних рівнянь з двома змінними; сформувати вміння розв’язувати системи рівнянь графічним способом; – розвивальна: формувати вміння аналізувати інформацію; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, скрупульозність; Тип уроку : засвоєння нових […]...
- Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними УРОК № 30 Тема. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про зміст означень: графік рівняння з двома змінними, система рівнянь з двома змінними, розв’язок системи рівнянь з двома змінними, а також алгоритмів побудови графіка рівняння з двома змінними та графічного способу розв’язування системи […]...
- Задачі на пропорційне ділення. Розв’язування рівнянь і нерівностей (№№ 849-857) Тема. Задачі на пропорційне ділення. Розв’язування рівнянь і нерівностей (№№ 849-857). Мета. Закріплювати вміння учнів розв’язувати задачі на пропорційне ділення; вчити складати задачі на пропорційне ділення за коротким записом; удосконалювати вміння розв’язувати рівняння і нерівності. Обладнання. Таблиця усних обчислень; картки для опитування; схеми задач. Зміст уроку І. Контроль, корекція і закріплення знань. 1. Перевірка домашнього […]...
- Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною УРОК № 14 Тема. Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною Мета уроку: закріплення учнями знань змісту понять: нерівність з однією змінною, розв’язок нерівності з однією змінною та що означає розв’язати нерівність з однією змінною; система нерівностей з однією змінною, розв’язок системи нерівностей з однією змінною та що означає розв’язати систему нерівностей з […]...
- Розв’язування систем рівнянь Математика – Алгебра Розв’язування систем рівнянь Розглянемо системи рівнянь, в яких одне або обидва рівняння другого степеня. 1. Щоб розв’язати систему рівнянь графічним способом, треба побудувати в одній системі координат графіки обох рівнянь системи й знайти координати точок перетину графіків. Ці точки і будуть розв’язками системи рівнянь. Наприклад: Графіком першого рівняння є коло з центром […]...
- Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Урок № 75 Тема. Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Мета: закріпити знання алгоритму розв’язування систем лінійних, рівнянь із двома змінними способом підстановки; вдосконалити вміння і навички, необхідні для застосування названого алгоритму; повторити матеріал попередньої теми щодо кількості розв’язків системи лінійних рівнянь залежно від співвідношення відповідних коефіцієнтів рівнянь. Тип уроку: засвоєння вмінь […]...
- Розв’язування нерівностей, що містять показникову функцію УРОК 49 Тема. Розв’язування нерівностей, що містять показникову функцію Мета уроку. Познайомити учнів зі способами розв’язування показникових нерівностей. І. Перевірка домашнього завдання Відповіді на запитання, що виникли в учнів під час виконання домашніх завдань. II. Аналіз самостійної роботи, проведеної на попередньому уроці ІІІ. Сприймання і усвідомлення розв’язування найпростіших показникових нерівностей та тих, що безпосередньо зводяться […]...
- Розв’язування систем рівнянь з двома змінними УРОК № 33 Тема. Розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про різні способи розв’язування систем рівнянь з двома змінними та випадки їх застосування. Закріпити вміння: за видом системи визначати оптимальний спосіб її розв’язування, описувати дії відповідно до обраного способу розв’язування системи рівнянь з двома змінними, а також виконувати дії відповідно […]...
- Розв’язання систем лінійних рівнянь способом підстановки Рівень А Відповідь: (1; 3). Відповідь: (7; -4,5). Відповідь: (1; 3). Відповідь: (4; 1). Відповідь: (3; 1). Відповідь: (1;-2). Відповідь: розв’язків немає. Відповідь: (3; 2). Відповідь: (4; 0). Відповідь: (3; 5). Відповідь: (1,5; 2). Відповідь: (3; -1). Відповідь: (7; 1). Відповідь: (1; -1). Рівень Б Відповідь: (2; 1,5). Відповідь: (1; -2). Відповідь: (20; 0,5). Відповідь: […]...
- Розв’язання систем лінійних рівнянь способом додавання Рівень А Відповідь: (4; 3). Відповідь: (-2; -3). Відповідь: (0,5; 1). Відповідь: (-1;2). Відповідь: (-2; 4). Відповідь: (5; 1). Відповідь: (3; -1). Відповідь: (0; -2). Відповідь: (-1; 3). Відповідь: (-1; -1). Відповідь: (2; -2). Відповідь: (4; -3). Відповідь: (-0,5; 0,5). Відповідь: (1; -1). Відповідь: (1; -2). Відповідь: (1; -2). Відповідь: (5; 6). Відповідь: (5; 0,5). […]...
- Розв’язування показникових нерівностей УРОК 50 Тема. Розв’язування показникових нерівностей Мета уроку. Формування умінь учнів розв’язувати показникові нерівності. І. Перевірка домашнього завдання 1. Відповіді на запитання, що виникли в учнів при виконанні домашніх завдань. 2. Усне розв’язування показникових нерівностей з використанням таблиці 21 для усних обчислень “Показникові нерівності “. 1 2 3 4 5 1 2х > 8 2х […]...
- Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 28. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Графічний спосіб розв’язування систем рівнянь є досить громіздким і до того ж не завжди допомагає знайти точні розв’язки. Розглянемо інші (не графічні) способи розв’язування систем лінійних рівнянь з двома змінними, які називають аналітичними. Почнемо зі способу […]...
- Системи нерівностей з однією змінною Математика – Алгебра Нерівності Системи нерівностей з однією змінною Розв’язком системи нерівностей з однією змінною називають значення змінної, яке є розв’язком кожної нерівності даної системи. Розв’язати систему нерівностей означає знайти всі її розв’язки або показати, що їх немає. Щоб розв’язати систему нерівностей, кожну її нерівність поступово спрощують, замінюючи рівносильною. Розглянемо на простих прикладах, як застосувати […]...
- Розв’язування дробово-раціональних рівнянь УРОК 26 Тема. Розв’язування дробово-раціональних рівнянь Мета уроку: познайомити учнів з розв’язуванням дробово-раціональних рівнянь відносно тригонометричних функцій, формувати уміння учнів розв’язувати дробово-раціональні рівняння і проводити відбір коренів за допомогою одиничного кола. І. Перевірка домашнього завдання 1. Відповіді на запитання учнів, які виникли у них при виконанні домашнього завдання. 2. Розв’язування аналогічних вправ. Розв’яжіть рівняння: A) […]...
- Розв’язування систем лінійних рівнянь із двома змінними способом додавання Урок № 76 Тема. Розв’язування систем лінійних рівнянь із двома змінним способом додавання Мета: сформувати в учнів усвідомлення необхідності знання алгоритму розв’язування лінійних рівнянь способом додавання та розуміння кожного кроку в цьому алгоритмі; виробити вміння використовувати названий алгоритм під час розв’язування систем лінійних рівнянь. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент […]...
- Системи рівнянь із двома змінними. Графічний метод розв’язання систем двох лінійних рівнянь із двома змінними 1007. Розв’язком системи рівнянь є пара чисел (6; 4), бо – правильні рівності. 1008. Пара чисел (-5; 2) є розв’язком системи рівнянь бо – правильні рівності. 1009. а) (1; 4) _ розв’язок системи рівнянь, бо 1 + 4 = 5 – правильна рівність; 3 • 1 + 4 = 7 – правильна рівність. Б) (-1; […]...