Розв’язування задач на знаходження відстані між мимобіжними прямими
Урок 41
Тема. Розв’язування задач на знаходження відстані між мимобіжними прямими
Мета уроку: формування вмінь учнів у знаходженні відстані між двома мимобіжними прямими.
Обладнання: стереометричний набір, моделі куба і прямокутного паралелепіпеда.
Хід уроку
1. Фронтальна бесіда за контрольними запитаннями № 13-15 та перевірка правильності розв’язання домашньої задачі.
2. Математичний диктант.
Дано зображення куба: варіант 1 (рис. 229); варіант 2 (рис. 230). Ребро куба дорівнює а.
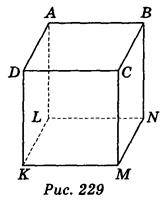
Знайдіть відстань між прямими:
1) АВ і LK;
2) АХ і CN;
3) AN і KM;
4) DL і AB;
5) AL і ВК;
6) KN і АВ. (Кожне завдання – 2 бали)
Відповідь. Варіант 1. 1) а; 2) а; 3) а; 4) 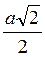 ; 5)
; 5) 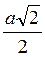 ; 6) а.
; 6) а.
Варіант 2. 1) а; 2) а; 3) 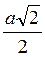 ; 4) а; 5)
; 4) а; 5) 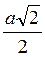 ; 6) а.
; 6) а.
Розв’язування задач, які допомагають знаходити відстань між двома мимобіжними прямими
Задача 1.
Відстань між мимобіжними прямими дорівнює відстані від однієї з цих прямих до паралельної цій прямій площини, яку проведено через другу пряму. Довести.
Відстань між мимобіжними
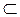 ?, b
?, b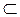 ?). Візьмемо довільну точку А на прямій а. Оскільки А
?). Візьмемо довільну точку А на прямій а. Оскільки А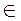 ?, то відстань від точки А до площини? дорівнює відстані між площинами? і?, а, отже, вона є відстанню між прямими а і b. Відстань від точки А до площини? є відстанню від прямої а до площини?.
?, то відстань від точки А до площини? дорівнює відстані між площинами? і?, а, отже, вона є відстанню між прямими а і b. Відстань від точки А до площини? є відстанню від прямої а до площини?.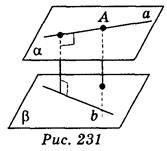
Задача 2.
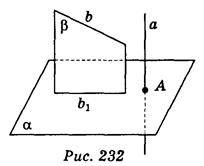
Відстань між мимобіжними прямими дорівнює відстані між їх проекціями на площину, перпендикулярну до однієї з цих прямих. Довести.
Нехай? А. Спроектуємо (ортогонально – перпендикулярно) обидві прямі а і b на площину? (рис. 232). Проекцією прямої а є точка А, а проекцію прямої b є пряма b1. Проведемо площину? через прямі b і b1. ? || ?, оскільки будь-яка проектуюча пряма площини? паралельна а. ?
А. Спроектуємо (ортогонально – перпендикулярно) обидві прямі а і b на площину? (рис. 232). Проекцією прямої а є точка А, а проекцію прямої b є пряма b1. Проведемо площину? через прямі b і b1. ? || ?, оскільки будь-яка проектуюча пряма площини? паралельна а. ? ?, тому перпендикуляр, проведений з точки А до прямої b1, буде перпендикуляром і до площини?. Цей перпендикуляр є відстанню від прямої а до паралельної їй площини?, а, отже, і відстанню між мимобіжними прямими а і b.
?, тому перпендикуляр, проведений з точки А до прямої b1, буде перпендикуляром і до площини?. Цей перпендикуляр є відстанню від прямої а до паралельної їй площини?, а, отже, і відстанню між мимобіжними прямими а і b.
1. Через вершину А трикутника ABC проведено пряму а, перпендикулярну до площини трикутника. Знайдіть відстань між прямими а і ВС, якщо АВ = 13 см, ВС = 14 см, АС = 15 см. (Відповідь. 12 см.)
2. До площини квадрата ABCD проведено перпендикуляр KD. Сторона квадрата дорівнює 5 см. Знайдіть відстань між прямими: 1) АВ і KD; 2) KD і АС. (Відповідь. 1) 5 см; 2) 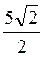 См.)
См.)
3. Прямокутники ABCD і АВМК лежать у різних площинах. Сума їх периметрів дорівнює 46 cm, AK = 6 cm, BC = 5 см. Знайдіть відстань між прямими AK і BC. (Відповідь. 6 см.)
4. Через точку перетину діагоналей квадрата ABCD проведено перпендикуляр МО до його площини; МО = а , АВ = 2а. Знайдіть відстань між прямими: 1) АВ і МО; 2) ВD і МС. (Відповідь. 1) а; 2) а.)
, АВ = 2а. Знайдіть відстань між прямими: 1) АВ і МО; 2) ВD і МС. (Відповідь. 1) а; 2) а.)
5. Ребро куба дорівнює 10 см. Знайдіть відстань між прямими а і b (рис. 233).
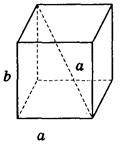
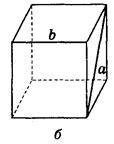
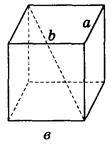
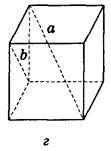
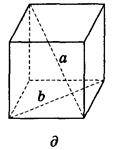
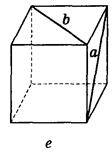
Рис. 233
(Відповідь: а) 5 см; б) 5
см; б) 5 см; в) 5
см; в) 5 см; г)
см; г) 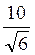 см; д)
см; д) 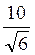 ; е)
; е) 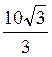 См.)
См.)
III. Домашнє завдання
§3, п. 21; контрольні запитання № 13-15. Розв’язати наступну задачу.
Через вершину С прямого кута трикутника АВС проведено пряму а, перпендикулярну до його площини. АС = 15 см, BC = 20 см. Знайдіть відстань між прямими а і АВ. (Відповідь. 12 см.)
Повторити п. 13 § 2.
Запитання до класу
1) Як можна знайти відстань між двома даними мимобіжними прямими?
2) Через вершину А прямокутного трикутника АВС з прямим кутом С проведено перпендикуляр SA до площини трикутника, СК – висота трикутника. Відомо, що АС = 3 см, АВ = 5 см. Укажіть, які з наведених тверджень правильні, а які – неправильні:
А) спільним перпендикуляром прямих SA і ВС є відрізок АВ;
Б) відстань між прямими SA і ВС дорівнює 3 см;
В) відстань між прямими SA і СК дорівнює відстані між точкою А і прямою СК;
Г) відстань між прямими SA і СК дорівнює 1,8 см.