Скалярний добуток векторів
УРОК № 49
Тема. Скалярний добуток векторів
Мета уроку: формування поняття скалярного добутку векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13].
Вимоги до рівня підготовки учнів: формулюють означення скалярного добутку, його властивості; застосовують вивчені означення та властивості до розв’язування задач.
Хід уроку
І. Перевірка домашнього завдання
Дано два вектори:
Варіант 1
 (1; 0),
(1; 0),  (0; -1);
(0; -1);
Варіант 2
 (-1; 0),
(-1; 0),  (0; 1).
(0; 1).
Знайдіть:
А) координати вектора 2 ;
;
Б) координати вектора –
 ;
;
В) довжину вектора  +
+  ;
;
Г) довжину вектора  –
–  ;
;
Д)
 + 4
+ 4 ;
;Є) довжину вектора 3 + 4
+ 4 .
.
ІІ. Аналіз результатів самостійної роботи
ІІІ. Поетапне сприймання й усвідомлення нового матеріалу
Скалярний добуток векторів
Скалярним добутком векторів  і
і  (позначення: (
(позначення: ( ?
? ), або
), або 
 , або (
, або ( ;
;  )) називається добуток довжин цих векторів на косинус кута між ними, тобто
)) називається добуток довжин цих векторів на косинус кута між ними, тобто  ?
? = |
= | | ? |
| ? | |cos? (рис. 211).
|cos? (рис. 211).
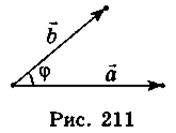
Два ненульові вектори тоді і тільки тоді взаємно перпендикулярні, коли їх скалярний добуток дорівнює нулю, тобто 
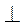

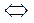
 ?
?  = 0 (
= 0 (
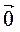 ,
, 
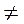
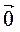 ).
).
Властивості скалярного добутку
1)  ?
? =
=  ?
? (переставний закон); 2)
(переставний закон); 2)  2 = |
2 = | |2, або |
|2, або | | =
| = 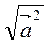 =
= 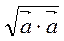 ; 3) (
; 3) ( +
+  ) ?
) ?  =
=  ?
? +
+  ?
? (розподільний закон); 4) (?
(розподільний закон); 4) (? ) ?
) ?  = ?(
= ?( ?
? ) (сполучний закон).
) (сполучний закон).
Примітка 1. Косинус кута між ненульовим векторами  та
та  виражається формулою
виражається формулою 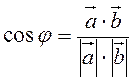 , яка випливає з означення скалярного добутку.
, яка випливає з означення скалярного добутку.
Примітка 2. Властивість 2 скалярного добутку, а саме формула | | =
| = 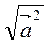 = =
= = 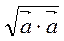 , дозволяє обчислювати довжину вектора в загальному випадку.
, дозволяє обчислювати довжину вектора в загальному випадку.
Примітка 3. Розподільний закон справджується для будь-якого скінченного числа доданків. Наприклад, правильна формула ( +
+  +
+ 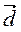 ) ?
) ?  =
=  ?
? +
+  ?
? +
+ 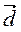 ?
? .
.
Скалярний добуток двох векторів, які задано координатами, дорівнює сумі добутків відповідних координат.
Якщо задано вектори  (a1; a2) і
(a1; a2) і  (b1; b2) на площині, то
(b1; b2) на площині, то  ?
? = а1b1 + а2b2.
= а1b1 + а2b2.
Розв’язування задач
1. Сторона рівностороннього трикутника ABC дорівнює 13. Знайдіть скалярний добуток  ?
? (рис. 212).
(рис. 212).
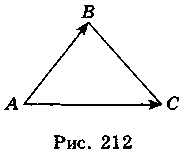
Розв’язання
Оскільки | | = |
| = |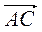 | = 13,
| = 13,  A = 60°, то
A = 60°, то  ?
?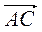 = |
= | |?|
|?|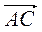 |cos
|cos A = = 13 ? 13 cos60° = 169 ?
A = = 13 ? 13 cos60° = 169 ?  = 84,5.
= 84,5.
Відповідь. 84,5.
2. Задано вектори 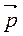 =
=  – 4
– 4 ,
, 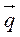 = 3
= 3 + 2
+ 2 , які взаємно перпендикулярні. Вектори
, які взаємно перпендикулярні. Вектори  і
і  – одиничні вектори. Знайдіть кут між векторами
– одиничні вектори. Знайдіть кут між векторами  і
і  (в градусах).
(в градусах).
Розв’язання
Оскільки | | = 1 і
| = 1 і 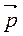 ?
? 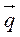 = 0, то маємо
= 0, то маємо 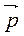 ?
?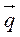 = (
= ( – 4
– 4 )(3
)(3 + 2
+ 2 ) = 3
) = 3 2 + 2
2 + 2
 – 12
– 12
 – 8b2 = 3 ? |
– 8b2 = 3 ? | |2 – 10|
|2 – 10| ||
|| | соs? – 8|
| соs? – 8| |2 = 3 – 10cos? – 8 = – 5 – 10cos?,
|2 = 3 – 10cos? – 8 = – 5 – 10cos?,
Тоді – 5 – 10cos? = 0, соs? = –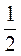 , ? = 120°.
, ? = 120°.
Відповідь. 120°.
IV. Розв’язування задач
1. Знайдіть кут між векторами  (1; 2) і
(1; 2) і 
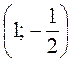 . 2. Дано вершини трикутника ABC: А
. 2. Дано вершини трикутника ABC: А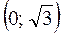 , В
, В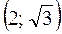 , С
, С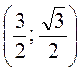 . Знайдіть його кути. 3. Доведіть, що вектори
. Знайдіть його кути. 3. Доведіть, що вектори  (т; п) і
(т; п) і  (-n; m) перпендикулярні або дорівнюють нулю. 4. Дано вектори
(-n; m) перпендикулярні або дорівнюють нулю. 4. Дано вектори  (3; 4) і
(3; 4) і  (m; 2). При якому значенні т вони перпендикулярні? 5. Дано вектори
(m; 2). При якому значенні т вони перпендикулярні? 5. Дано вектори  (1; 0) і
(1; 0) і  (1; 1). Знайдіть таке число х, щоб вектор
(1; 1). Знайдіть таке число х, щоб вектор  + x
+ x був перпендикулярний до вектора
був перпендикулярний до вектора  . 6. Доведіть, що коли
. 6. Доведіть, що коли  і
і  – одиничні неколінеарні вектори, то вектори
– одиничні неколінеарні вектори, то вектори  +
+  і
і  –
–  відмінні від нуля й перпендикулярні. 7. Дано вектори
відмінні від нуля й перпендикулярні. 7. Дано вектори  і
і  . Знайдіть абсолютну величину вектора
. Знайдіть абсолютну величину вектора  +
+  , якщо |
, якщо | | = |
| = | | = 1, а кут між векторами
| = 1, а кут між векторами  і
і  дорівнює 60°.
дорівнює 60°.
V. Домашнє завдання
1. Вивчити теоретичний матеріал. 2. Розв’язати задачу.
Дано вершини трикутника A(1; 1), B(4; 1), С(4; 5). Знайдіть косинуси кутів цього трикутника.
VI. Підбиття підсумків уроку
Завдання класу
1. Дайте означення скалярного добутку векторів та сформулюйте властивості скалярного добутку векторів. 2. Сформулюйте властивість і ознаку перпендикулярних векторів.