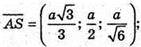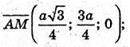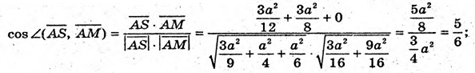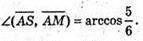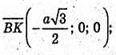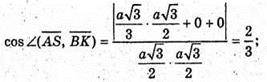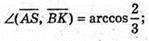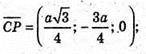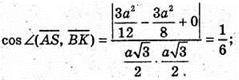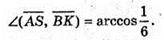Головна ⇒ 📌ГДЗ з математики ⇒ Скалярний добуток векторів. Кут між векторами
Скалярний добуток векторів. Кут між векторами
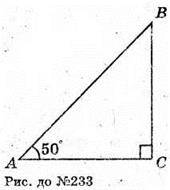
233.
А) Якщо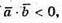 
то α = 90°, α – кут між векторами.
Б) то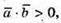 
α – гострий;
А) то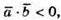 
α – тупий.
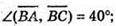
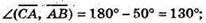
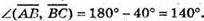
234.
А)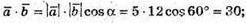 
Б) 
В)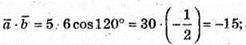 
Г)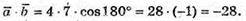 
235.
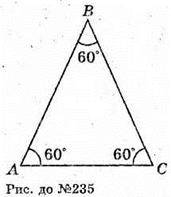
А)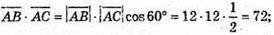 
Б)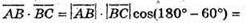 
236.
А)
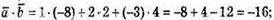
Б)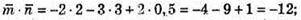 
В)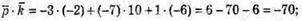 
Г)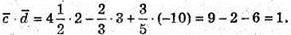 
237.
А)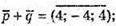 
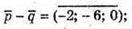
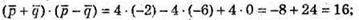
Б)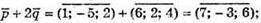 
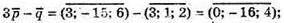
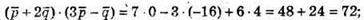
В)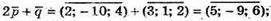 
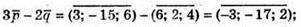
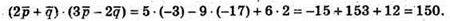
238.
α – кут між векторами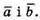 
А)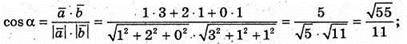
Б)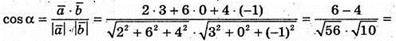 
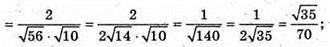
В)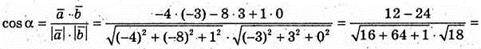 
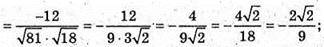
Г)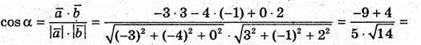 
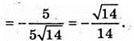
239.
А)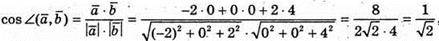 
Звідси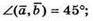 
Б)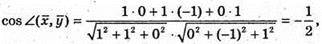 
Звідси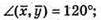 
В)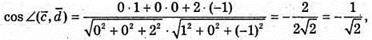 
Звідси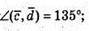 
Г)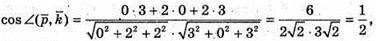 
Звідси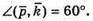 
240.
А(2; 1; 3), В(7; 4; 5), С(4; 2; 1)
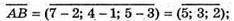
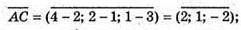
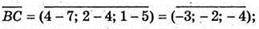
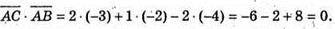
Отже,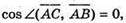 
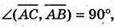
Тобто ∠C = 90°, а тому ΔABC – прямокутний.
241.
А)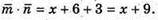 
Якщ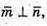о 
то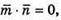 
тобто х + 9 = 0;
Х = -9. Отже,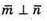 
при х = -9.
Б)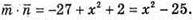 
Оскільки 
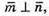то x2 – 25 = 0: х2 = 25;
X = 5 або x = -5;
В)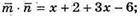 
x+ 2 + 3x – 6 = 0; 4x = 4; x = 1. При х = 1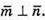 
Г)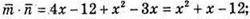 
x2 + x – 12 = 0; x = 3; x = -4.
Отже, при x = 3 або x = -4 вектори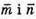 
перпендикулярні.
242.
Нехай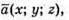 
тоді 
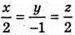(оскільки 
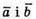– колінеарні).
Звідси x = -2y; z = -2у.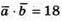 
(за умовою).
Тому: 2x – у + 2z = 18 або 2 × (-2y) – y + 2 × (-2у) = 18;
-9y = 18; у = -2. Тоді x = -2 × (-2) = 4; z = -2 × (-2) = 4. Отже, а(4; -2; 4).
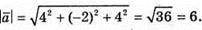
243.
α – кут між векторами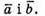 
А)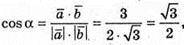 
звідси α = 30°;
Б)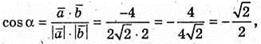 
звідси α = -135°.
244.
А)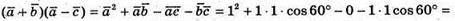 
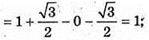
Б)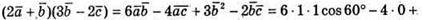 
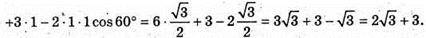
245.
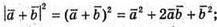
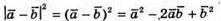
А)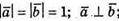 
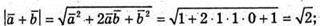
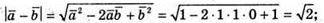
Б)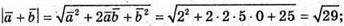 
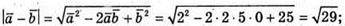
В)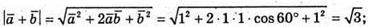
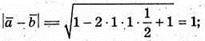
Г)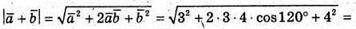
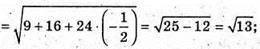
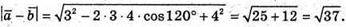
246.
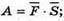
247.
А)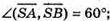 
Б)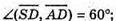 
В)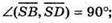 
Г)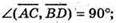 
Г)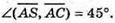 
248.
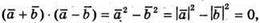якщо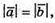 
тоді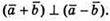 
249.
А)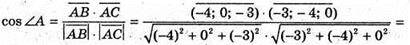 
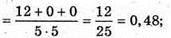
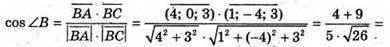
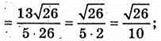
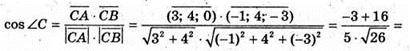
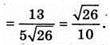
Б)
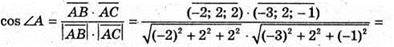
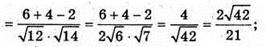
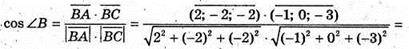
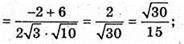
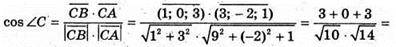
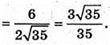
250.
A(1; 4; 8), В(-4; 0; 3), O(0; 0; 0).
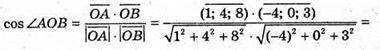
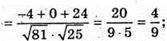
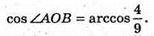
251.
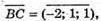А(0; 2; -1)
А) Нехай 0(х; 0; 0), тоді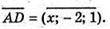 
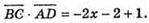
Оскільки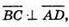 
то -2х -2 + 1 = 0; -2х = 1; х = -0,5.
Отже, О(-0,5; 0; 0).
Б) Нехай D(0; у; 0), тоді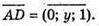 
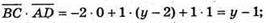у -1 = 0; у = 1. Отже, D(0; 1; 0).
В) Нехай D(0; 0; z), тоді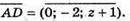 
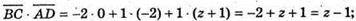
Z – 1 = 0; z = 1. Отже, O(0; 0; 1).
252.
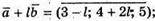
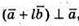тому 3 × (3 – l) + 4(4 + 2l) + 5 × 5 = 0;
9 – 3l + 16 + 8l + 25 = 0; 5l = -50; l = -10.
253.
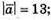
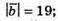
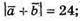
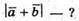
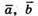– сторони паралелограма,
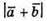і 
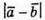– діагоналі паралелограма.
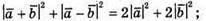
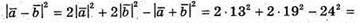
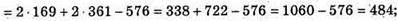
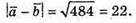
254.
А)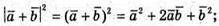 
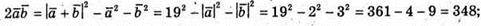
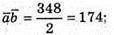
Б)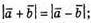 
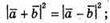
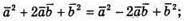
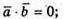
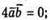
В)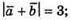 
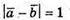
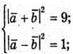
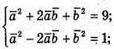
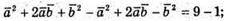
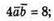
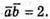
255.
А)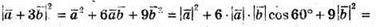 
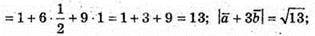
Б)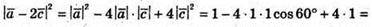 
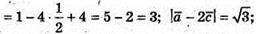
В)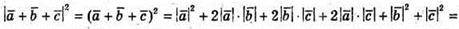 
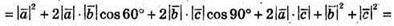
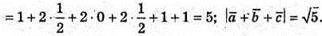
256.
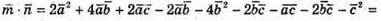
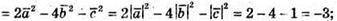
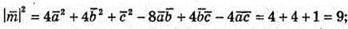
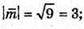
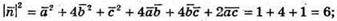
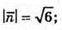
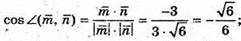
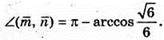
257.
Нехай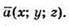 
Тоді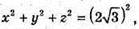 
х – 2у + z = 0 і 2х + у – 3z = 0.
Маємо систему: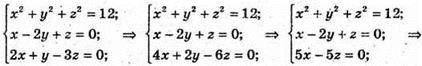 
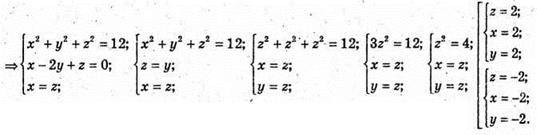
Отже,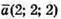 
або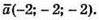 
258.
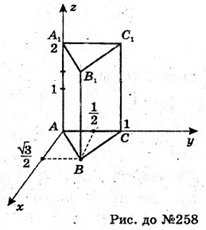
Розмістимо призму в системі координат, як показано на рисунку.
Тоді А(0; 0; 0),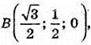 
С(0; 1; 0),A1 (0: 0; 2),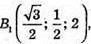 
С 2 (0; 1; 2).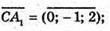 
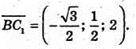
А)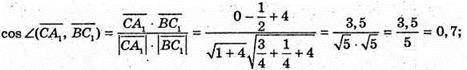 
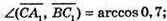
Б)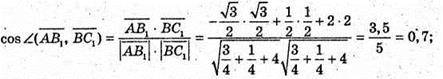 
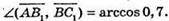
259.
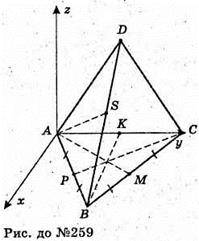
Розмістимо тетраедр в системі координат, як показано на рисунку,
А – ребро тетраедра. А(0; 0; 0); С(0; а; 0);
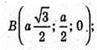
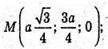
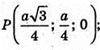
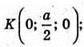
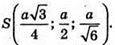
Знайдемо кут між AS і AM. 
(1 votes, average: 5.00 out of 5)
Loading...Related posts:
- Кут між векторами. Скалярний добуток векторів Урок 59 Тема. Кут між векторами. Скалярний добуток векторів Мета уроку: формування понять кута між векторами, скалярного добутку векторів. Формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі” Хід уроку 1. Фронтальна бесіда з класом за контрольними запитаннями № 18- 20 з використанням схеми “Вектори в просторі” (див. с. 233). […]...
- Скалярний добуток векторів Геометрія Вектори Скалярний добуток векторів Скалярним добутком векторів і називається число . Позначення: . . Очевидно, що . Розподільна властивість скалярного добутку: . Кутом між ненульовими векторами і називається кут BAC. Кутом між будь-якими двома ненульовими векторами і називається кут між векторами, що дорівнюють даним і мають спільний початок. Вважають, що кут між однаково напрямленими […]...
- Скалярний добуток векторів УРОК № 49 Тема. Скалярний добуток векторів Мета уроку: формування поняття скалярного добутку векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: формулюють означення скалярного добутку, його властивості; застосовують вивчені означення та властивості до розв’язування […]...
- Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Урок 58 Тема. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Мета уроку: формування знань учнів про вектори в просторі, дії над векторами, заданими координатами, Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі”. Хід уроку І. Перевірка домашнього […]...
- Векторний добуток векторів 1. Векторний добуток векторів є вектором, а скалярний – числом. Векторний та скалярний добуток мають однакові властивості (крім комутативності). 2. За означенням модуля векторного добутку А отже, оскільки то 3. 1) За означенням У нашому випадку Скористаємось основною тригонометричною тотожністю: Тоді 2) За означенням У нашому випадку Скористаємось основою тригонометричною тотожністю: Тоді Оскільки 3) Рівність […]...
- Застосування векторів 269. 5(х – 2) + 0 × (у + 1) – 3(z – 4) = 0; 5x – 10 – Зz + 12 = 0; 5x – Зz + 2 = 0 – рівняння шуканої площини. 270. 3(x – 1) – 4(y – 2) + 7(z + 3) = 0; 3x – 3 – 4у […]...
- Розв’язування задач на застосування векторів Урок 60 Тема. Розв’язування задач на застосування векторів Мета уроку: формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: стінна таблиця “Вектори в просторі”. Хід уроку І. Перевірка домашнього завдання 1. Два учні відтворюють розв’язування задач № 55 (4), 56. 2. Фронтальне опитування. 1) Чому дорівнює скалярний добуток векторів, які задано координатами? 2) Як […]...
- Дії над векторами 192. А) Б) В) Г) 193. 194. А) Б) В) 195. 196. бо – протилежні вектори, (аналогічно). 197. 198. А) Б) 199. А) Але оскільки – однаково напрямлені і Отже, Б) 200. 201. А) Б) В) Г) Г) 202. А) Б) В) 203. А) Б) 204. А) Б) 205. 206. Отже, а = 2, b […]...
- Координати вектора. Дії над векторами, що задані координатами 1. Запишемо координати вектора: 1) 2) 3) 4) 2. 1) 2) 3) 4) 5) 6) 3. 1) Запишемо розклад за координатними векторами: 2) Запишемо розклад за координатними векторами: 3) Запишемо розклад за координатними векторами: 4) Знайдемо координати векторів : Знайдемо координати вектора Запишемо розклад за координатними векторами: 5) Знайдемо координати векторів Знайдемо координати вектора Запишемо […]...
- Додавання векторів за правилом паралелограма – Елементи векторної алгебри 3. Елементи векторної алгебри 3.2. Додавання векторів за правилом паралелограма Щоб додати два вектори за правилом паралелограма, треба розмістити їх так, не змінюючи їх напряму, щоб вони виходили з однієї точки, й добудувати на кінцях векторів паралельні прямі. Діагональ одержаного паралелограма, проведена з точки, в якій суміщені початки обох векторів, є їх сумою....
- Застосування координат 124. Б) 0 ≤ x ≤ 4; 0 ≤ у ≤ 4; 0 ≤ z ≤ 4. 125. 0 ≤ х ≤ 3; 0 ≤ у ≤ 3; -3 ≤ 2 ≤ 3. 126. А) А(0; 0; 0); В(0; 1; 0); С(1; 1; 0); D(1; 0; 0); А1(0; 0; 1); В1(0; 1; 1); С1(1; 1; […]...
- Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...
- Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...
- Суміжні та вертикальні кути § 1. Найпростіші геометричні фігури та їхні властивості § 4. Суміжні та вертикальні кути Практичні завдання 86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС. ∠АОВ – прямий, ∠COA – суміжний до кута АОВ. ∠BOC – тупий, ∠AOB – суміжний до кута ВОС. 87. ∠AOC і ∠COB – суміжні. 88. а) ∠ABD i ∠CBD; […]...
- Добуток різниці та суми двох виразів Рівняння коренів не має; Коренем рівняння є будь-яке число; Отже, значення виразу не залежить від значення змінної. 2) (2a – b)(2a + b) + (b – с)(b + с) + (с – 2а)(с + 2а) = 4а2 – b2 + b2 – с2 + с2 – 4а2 = 0. Отже, значення виразу не залежить від […]...
- Додавання векторів Геометрія Вектори Додавання векторів Сумою векторів і називається вектор . Додавання векторів має переставну та сполучну властивості: ; для будь-яких , , . Теорема. Які б не були точки A, B, C, справджується векторна рівність: . Правило трикутника додавання векторів Щоб знайти суму довільних векторів і , треба від кінця вектора (див. рисунок) відкласти вектор […]...
- Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...
- Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...
- Відрізок і його довжина § 1. Найпростіші геометричні фігури та їхні властивості 2. Відрізок і його довжина Практичні завдання 20. Точки С, D, Е належать відрізку AB, а точки F, M, K не належать відрізку АВ. 21. Утворилося три відрізки АВ, ВС, АС. 22. Точка С лежить між точками А і В, а точка D – між точками В […]...
- Відрізок. Вимірювання відрізків. Відстань між двома точками Розділ 1. Елементарні геометричні фігури та їхні властивості § 2. Відрізок. Вимірювання відрізків. Відстань між двома точками 13. На рисунку зображені відрізки: AB, AK, BK, ВМ. AK = 38 мм, MB = 12 мм. 14. На рисунку зображені відрізки: PC, PD, CD, PT. PC = 9 мм. PD = 31 MM. PT = 27 мм. […]...
- Додавання векторів УРОК № 44 Тема. Додавання векторів Мета уроку: формування вміння додавати вектори, вивчення властивостей суми векторів; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують додавання векторів; відкладають вектор, що дорівнює сумі векторів; формулюють […]...
- Алгебра векторів 1. Побудуємо вектори – одиничний вектор 2. Побудуємо вектори 3. Побудуємо вектори 4. Побудуємо вектори 5. 6. 1) Побудуємо вектори 2) Побудуємо вектори 7. Побудуємо вектори 8. 1) 2) 9. Побудуємо вектори Вектори та рівні. 10. Накреслимо два ненульові вектори Побудуємо Побудуємо Таким чином, 11. Побудуємо вектори Вектори протилежно напрямлені. 12. Побудуємо вектори 13. 1) […]...
- Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...
- Тематична контрольна робота № 5 УРОК № 51 Тема. Тематична контрольна робота № 5 Мета уроку: контроль навчальних досягнень учнів з мети “Вектори”. Тип уроку: комбінований. Вимоги до рівня підготовки учнів: застосовують означення та властивості геометричних фігур при розв’язуванні задач. Хід уроку І. Тематичне оцінювання № 5 Тематичне оцінювання № 5 можна провести у вигляді тематичної контрольної роботи. Наводимо текст […]...
- Вектори у просторі 156. ABCDEF – правильний шестикутник. А) Б) В) Але 157. 158. А) Б) В) 159. 160. А) Б) В) 161. 162. А(х; у; z). Тому -5 – х = З, x = -8; 4 – у = 4, у = 0; 1 – z = 2, z = -1. Отже, А(-8; 0; -1). 163. С(-2; […]...
- Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...
- Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...
- Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...
- Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...
- Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...
- Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...
- Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...
- Промінь. Кут. Вимірювання кутів § 1. Найпростіші геометричні фігури та їхні властивості 3. Промінь. Кут. Вимірювання кутів Практичні завдання 49. Промені AB і АС – не доповняльні. Промінь AN – доповняльний до променя AB, а промінь AM – доповняльний до променя АС. На рисунку зображено промені АB, АС, AN, AM. 50. Промені AB і ВА не е доповняльними, оскільки […]...
- Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною Розділ 2. Взаємне розміщення прямих па площині § 10. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною 199. 1) ∠1 = ∠8, ∠6 = ∠3 (як відповідні кути при паралельних прямих а і b і січній с). 2) ∠2 = ∠4 (як внутрішні різносторонні кути при паралельних прямих а і b і […]...
- Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...
- Прямокутна система координат 11. 12. Точки А(4; 4; 4), В(-4; 4; 4), С(-4;-4; 4), П(4; 4; -4), D(-4; 4; -4), E(4; -4; 4), F(4; -4; -4), M(-4; -4; -4) віддалені від кожної з координатних площин на 4. 13. 14. О – початок координат. ОВ > ОА, отже, ближче до початку координат лежить т. А. 15. 16. Оскільки КТ […]...
- Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...
- Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...
- Розкладання многочлена на многочлени. Винесення спільного множника за дужки 437. 1) Якщо х = 4,32, то 6,32х – х2 = х(6,32 – х) = 4,32 • (6,32 – 4,32) = 4,32 • 2 = 8,64. 2) Якщо а = 1,5, b = -2,5, то а3 + а2b = а2(а + b) = 1,52 • (1,5 – 2,5) = 2,25 • (-1) = -2,25. 3) […]...
- Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...