Теорема косинусів
УРОК № 4
Тема. Теорема косинусів
Мета уроку: вивчення теореми косинусів. Формування вмінь учнів застосовувати теорему косинусів до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13].
Вимоги до рівня підготовки учнів: формулюють теорему косинусів та доводять її.
Хід уроку
I. Перевірка домашнього завдання
Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів у ході їх розв’язування.
ІІ.
ІІІ. Мотивація навчальної діяльності
Ми приступаємо до вивчення теми “Розв’язування трикутників”.
Розв’язати трикутник означає знайти відомі елементи трикутника (сторони, кути) за даними відомими елементами. У 8-му класі ви вже навчилися розв’язувати прямокутні трикутники. Прямокутний трикутник визначається за двома елементами, серед яких є хоча б один лінійний елемент (сторона). Ви вмієте знаходити невідомі елементи прямокутного трикутника, якщо дано: катет і гіпотенузу; гіпотенузу і гострий кут; катет і прилеглий гострий кут; катет і протилежний
Щоб розв’язати довільний (не прямокутний) трикутник, треба знати три елементи, серед яких має бути хоча б один лінійний.
Зараз ви ознайомитеся з теоремою, яка дозволяє за двома сторонами і кутом між ними знаходити третю сторону, невідомі кути трикутника. Ця теорема називається теоремою косинусів.
IV. Сприймання й усвідомлення нового матеріалу
Вивчення теореми косинусів
Сформулюємо теорему та ознайомимо з її доведенням учнів.
Теорема. Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.
Доведення
Нехай задано трикутник ABC, доведемо, що а2 = b2 + с2 – 2bc cos?, де а = ВС, b = AC, с = АВ, 
A = ?.
Розглянемо три випадки: якщо кут А є гострим, тупим і прямим.
1-й випадок
Якщо кут А гострий (рис. 8), то проведемо висоту BD і розглянемо прямокутний трикутник BDC. У ньому ВС2 = DC2 + BD2 або a2 = (b – b1)2 + h2. (1)
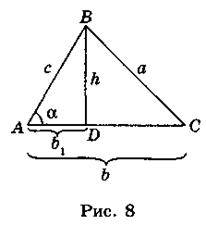
Виразимо b1 і h через основні елементи трикутника ABC. Із трикутника ABD миємо: h = csin?, b1 = ccos?. Замінивши h і b1 у виразі (1) їх значеннями, знайдемо:
A2 = (b – ccos?)2 + с2sin2? = b2 – 2bc cos? + с2cos2? + c2sin2? = b2 – 2bc cos? + c2(sin2? + cos2?) = b2 – 2bccos? + c2 – 1 = b2 + c2 – 2bc cos?.
Отже, a2 = b2 + c2 – 2bc cos?, що і треба було довести.
2-й випадок
Нехай кут А тупий (рис. 9). Із вершини В проведемо висоту BD на продовження сторони АС. Із прямокутного трикутника BDC маємо:
BC2 = BD2 + DC2 або a2 = h2 + (b + b1)2. (2)
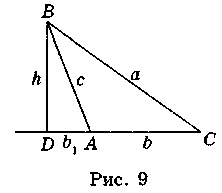
Значення h і b1 виразимо через основні елементи трикутника ABC. Із трикутника ABD маємо: h = csin(180°- ?) = csin?, b1 = ccos(180° – ?) = – ccos?. Замінивши h і b1 у виразі (2) їх значеннями, після деяких перетворень маємо:
A2 = c2sin2? + (b – ccos?) = с2sin2? + b2 – 2bc cos? + c2cos2? = (c2sin2? + c2cos2?) + b2 – 2bc cos? = c2(sin2? + cos2?) + b2 – 2bc cos? = b2 + c2 – 2bc cos?.
Отже, a2 = b2 + c2 – 2bc cos?, що і треба було довести.
3-й випадок
Нехай кут А прямий, ? = 90° (рис. 10). У цьому випадку cos? = cos 90° = 0, отже, маємо:
B2 + c2 – 2bc cos? = b2 + c2 – 2bc – 0 = b2 + с2. (3)
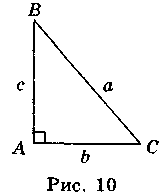
Але за теоремою Піфагора маємо: b2 + с2 = а2. (4)
Порівнявши вирази (3) і (4), отримаємо: a2 = b2 + c2 – 2bc cos?. Теорему, доведено.
Теорему косинусів іноді називають узагальненою теоремою Піфагора. Така назва пояснюється тим, що в теоремі косинусів міститься як частковий випадок теорема Піфагора. Справді, якщо в трикутнику ABC кут А прямий, то cos A = cos 90° = 0, і за теоремою косинусів одержуємо а2 = b2 + с2, тобто квадрат гіпотенузи дорівнює сумі квадратів катетів.
Розв’язування задач
При розв’язуванні цих задач слід домовитися, що сторони трикутника позначатимемо буквами a, b, с, а протилежні їм кути (при вершинах А, В, С) – грецькими літерами?, ?, ?. Слід також згадати значення тригонометричних функцій деяких кутів (табл. 1), зазначивши, що синуси суміжних кутів рівні, а косинуси суміжних кутів – протилежні числа: sin(180°- ?) = sin?, cos(180°- ?) = – cos?. Розв’яжемо такі задачі.
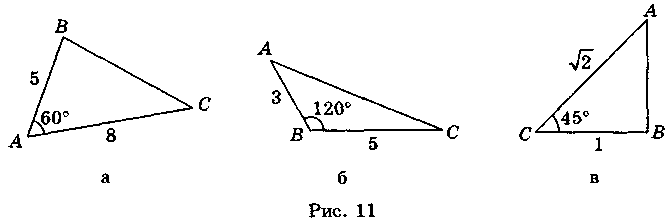
1. Дві сторони трикутника дорівнюють 
см і 1 см, а кут між ними 30°. Знайдіть третю сторону трикутника. (Відповідь. 1 см.) 2. Знайдіть третю сторону трикутника, якщо дві інші сторони дорівнюють 1 см і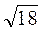 
см і утворюють кут 135°. (Відповідь. 5 см.)
V. Закріплення й осмислення нового матеріалу
Розв’язування задач
1. Сторони трикутника дорівнюють 1 см, 3
см і 5 см. Знайдіть кут, який лежить проти найбільшої сторони.
Розв’язання
Нехай у трикутнику ABC а = 1 см, b = 3 см, с = 5 см. За теоремою косинусів маємо: с2 = b2+ a2 – 2ba cos?, тоді 52 = 12 +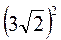 
– 2 – 1 – 3Cos?; 25 = 19 – 6Cos?; 6Cos? = – 6; cos? =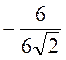 
= 
= 
;
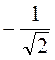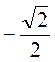Тоді? = 180° – 45° = 135°.
Відповідь. 135°.
2. Дві сторони трикутника а і с дорівнюють 5 см і 7 см, а кут? дорівнює 60°. Знайдіть сторону b.
Розв’язання
За теорему косинусів маємо:
С2 = а2 + b2 – 2ab cos?, або 72 = 52 + b2 – 2 – 5 – bcos60°, звідси 49 = 25 + b2 – 5b, або b2 – 5b – 24 = 0. Розв’язавши рівняння, одержимо b1 = 8; b2 = -3. Оскільки b > 0, то значення b2 не задовольняє умову задачі.
Відповідь. 8 см.
3. У трикутнику дві сторони дорівнюють 5 м і 6 м, а синус кута між ними дорівнює 0,6. Знайдіть третю сторону.
Розв’язання
Нехай а = 5 м, b = 6 м, sin? = 0,6. Оскільки sin2? + cos2? = 1, то 0,36 + cos2? = 1, cos2? = 0,64 і cos? = ±0,8.
1-й випадок:
Cos? = 0,8. Тоді с2 = а2 + b2 – 2abcos? = 25 + 36 – 2 – 5 – 6 – 0,8 = 61 – 48 = 13; с =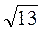 
м.
2-й випадок:
Cos? = -0,8. Тоді с2 = а2 + b2 – 2abcos? = 25 + 36 + 2 – 5 – 6 – 0,8 = 61 + 48 = 109; с =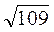 
м.
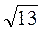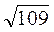Відповідь. м або м.
VI. Домашнє завдання
1. Вивчити теорему косинусів. 2. Розв’язати задачу.
Сторони трикутника дорівнюють 5 м, 6 м і 7 м. Знайдіть косинуси кутів трикутника.
VII. Підбиття підсумків уроку
Завдання класу
1. Сформулюйте теорему косинусів. 2. Знайдіть невідому сторону трикутника (рис. 11).
(1 votes, average: 5.00 out of 5)
Loading...