Головна ⇒ 📌Довідник з математики ⇒ Узагальнення поняття степеня

Узагальнення поняття степеня

Математика – Алгебра

Степенева функція

Основнi означення

1. Якщо n Є N, 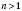, то 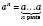, де a – довільне число.
2. 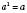, де а – довільне число.
3. 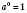для 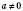. 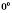не має змісту.
4. 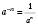, n Є N, .
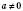5. 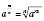, n Є N, m Є Z, .

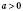Властивості степеня з раціональним

показником

Для будь-яких раціональних чисел r і s і будь-яких додатних a і b виконуються такі рівності.
1. .
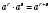2. .
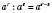3. .
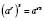4. .
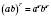5. .
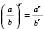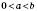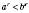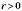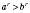6. Якщо , то для ; для .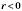
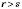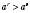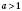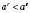7. Якщо , то для ; для .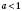

Поняття

степеня з ірраціональним показником

Нехай a – будь-яке додатне число, яке не дорівнює 1, – будь-яке ірраціональне число.
Розглянемо три випадки.
1. , .
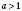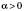Наприклад, 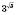; 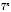. Степінь 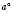означає таке число, яке більше від усякого степеня 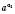, але менше від усякого степеня 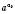, де 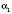– будь-яке раціональне наближення числа , взяте з недостачею, а 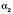– будь-яке наближення числа a, взяте з надлишком. Зверніть увагу: таке дійсне число існує, і до того ж єдине.
2. , .
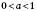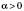Наприклад, 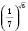. Тоді під степенем 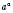розуміють число, яке менше від будь-якого степеня 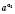, але більше від будь-якого степеня .
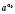3. a – довільне число, крім 1, .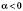
Наприклад, 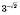, 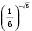. Тоді вважають .
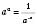Дії над степенями з ірраціональними показниками виконуються за тими самими правилами, які встановлені для степенів із раціональними показниками.

Степенева функція

Функцію 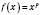, де x – змінна, а p – стале дійсне число, називають Степеневою функцією.
Властивості степеневої функції залежать від значення p.
1. p Є N. Тоді ; ;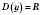
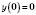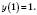
Якщо p – непарне, знак y збігається зі знаком x; функція непарна й зростає на всій області визначення. Якщо p – парне, 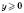для всіх значень x; функція парна. Якщо 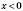, функція спадає, якщо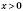, функція зростає.
2. p Є Z; 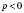. Тоді .
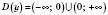Графік складається з двох віток; .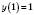
Якщо p – непарне, то для всіх значень 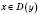знак функції збігається зі знаком аргументу.
Функція непарна, спадна на кожному з проміжків 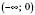і .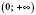
Якщо p – парне, 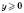для всіх x; функція парна. Якщо 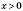, функція спадає, якщо 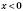, функція зростає. На рисунках, поданих нижче, наведені графіки степеневої функції для різних значень p:

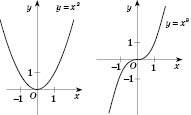
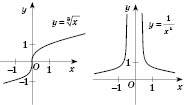
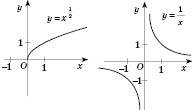
Показникова функція

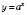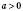Функція , де і 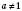, називається Показниковою (з основою а).
Властивості показникової функції
:

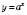
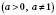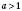
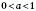
1. 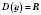. 1. .
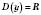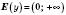2. . 2. .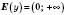
3. Функція не є ні парною, ні непарною.
4. Графік функції розміщений у верхній півплощині, перетинає вісь Oу у точці (0; 1), вісь Oх є для нього асимптотою.
5. Функція зростає 5. Функція спа на R. дає на R.
6. Якщ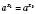о , то .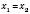
7. Якщо 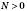, то існує, і до того ж єдине, значення x, при якому 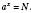(Тобто рівняння 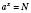завжди має розв’язок, і до того ж єдиний, якщо , , .)
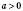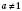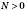На рисунку внизу зліва зображений графік показникової функції 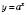при 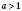; на рисунку 1 – при .

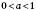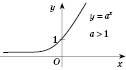
Рис. 1

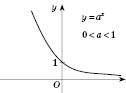
Рис. 2