Головна ⇒ 📌Довідник з математики ⇒ Властивості нескінченно малих послідовностей
Властивості нескінченно малих послідовностей
Математика – Алгебра
Границя
Властивості нескінченно малих послідовностей
Теорема 1. Алгебраїчна сума скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю.
Послідовність 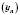 називається Обмеженою, якщо існує таке число
називається Обмеженою, якщо існує таке число 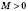 , що для всіх значень
, що для всіх значень 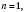 2, … виконується нерівність
2, … виконується нерівність 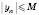 .
.
Теорема 2. Добуток нескінченно малої числової послідовності та обмеженої послідовності є нескінченно малою
Послідовність
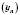 називається Нескінченно великою, якщо, яке б не було число
називається Нескінченно великою, якщо, яке б не було число 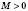 , існує таке число
, існує таке число 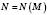 , що для всіх
, що для всіх 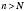 виконується нерівність
виконується нерівність 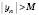 .
.Позначення:
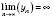 .
.Теорема 3. Якщо
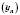 є нескінченно великою числовою послідовністю, то послідовність
є нескінченно великою числовою послідовністю, то послідовність 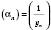 є нескінченно малою, і навпаки: якщо послідовність
є нескінченно малою, і навпаки: якщо послідовність 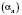 є нескінченно малою числовою послідовністю і
є нескінченно малою числовою послідовністю і 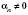 для всіх натуральних n, то послідовність
для всіх натуральних n, то послідовність 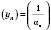 є нескінченно великою.
є нескінченно великою.Related posts:
- Границя числової послідовності Математика – Алгебра Границя Границя числової послідовності Число a називається Границею послідовності,, …, , …, якщо для будь-якого додатного числа існує таке натуральне число , що для всіх виконується нерівність . Позначеня: , або . Послідовність , , 2, … називається Нескінченно малою, якщо для будь-якого додатного числа ε існує натуральне число N таке, що […]...
- Границя функції Математика – Алгебра Границя Границя функції Нехай функція визначена на проміжку (можливо, що ). Число A називається границею функції у точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність . Позначення: , або . Нехай – внутрішня точка проміжку . Функція називається нескінченно малою […]...
- Числові послідовності. Властивості числових послідовностей УРОК № 49 Тема. Числові послідовності. Властивості числових послідовностей Мета уроку: домогтися засвоєння учнями змісту понять: числова послідовність, n-й член числової послідовності, формула п-го члена; списку способів задання числової послідовності. Виробити вміння: відтворювати вивчені означення; знаходити члени послідовності із заданими номерами, якщо послідовності задані різними способами. Повторити означення числової функції, а також супутні поняття. Тип […]...
- Основні теореми про границі числової послідовності Математика – Алгебра Границя Основні теореми про границі числової послідовності Теорема 1. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю . . Теорема 2. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю, яка дорівнює ab: . Наслідки 1) Сталий множник можна виносити за знак границі. […]...
- Властивості прогресій – ПРОГРЕСІЇ Формули й таблиці МАТЕМАТИКА ПРОГРЕСІЇ Нескінченною числовою послідовністю називається числова функція, визначена на множині натуральних чисел: Арифметична прогресія Геометрична прогресія Арифметичною прогресією називається така послідовність чисел, при якій кожен член, починаючи із другого, дорівнює попередньому, доданому до одного й того самого, постійного для цього ряду числа. Геометричною прогресією називається така послідовність чисел, при якій кожен […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Арифметична прогресія Математика – Алгебра Послідовності Арифметична прогресія Арифметичною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число. Це стале для даної послідовності число d називається Різницею арифметичної прогресії. Арифметична прогресія буде зростаючою, якщо , і спадною, якщо . Прогресію можна задати за допомогою першого члена […]...
- Кoрінь n-го степеня та його властивості Математика – Алгебра Степенева функція Кoрінь n-го степеня та його властивості Коренем N-го степеня з числаА називається таке число, n-й степінь якого дорівнює а. Якщо n – число непарне, то існує – і до того ж тільки один – корінь n-го степеня з довільного числа а. Цей корінь – число того ж знака, що число […]...
- Нерівності Математика – Алгебра Нерівності Число а вважається більшим від b, якщо різниця – число додатне. Число a менше від b, якщо різниця – число від’ємне. Якщо , то числа a і b рівні. На координатній прямій меншому числу відповідає точка, що лежить ліворуч від точки, яка відповідає більшому числу. Позначення: – a менше від b; […]...
- Паралельне перенесення та його властивості Геометрія Рух Паралельне перенесення та його властивості Перетворення фігури F, при якому довільна її точка з координатами переходить у точку , де a і b – одні й ті самі для всіх точок, називається Паралельним перенесенням. Теорема. Паралельне перенесення є рухом. При паралельному перенесенні пряма переходить у паралельну пряму (або в себе) (див. рисунок). Існування […]...
- Властивості модуля – Модуль і його властивості Математика – Алгебра Модуль і його властивості Модуль числа – це відстань від 0 до точки, що відповідає цьому числу на координатній прямій, виміряна в одиничних відрізках. Отже, для всіх значень a. Властивості модуля 1. . 2. Якщо , то . 3. Якщо , то 4. Модуль суми скінченного числа дійсних чисел не перевищує суми […]...
- Властивості числових нерівностей Математика – Алгебра Нерівності Властивості числових нерівностей a, b, с, d – довільні числа. 1. Якщо і , то . 2. Якщо до обох частин правильної нерівності додати одне й те саме число, то дістанемо правильну нерівність. 3. Якщо обидві частини правильної нерівності помножити на одне й те саме додатне число, то дістанемо правильну нерівність. […]...
- Геометрична прогресія Математика – Алгебра Послідовності Геометрична прогресія Геометричною прогресією називається послідовність відмінних від 0 чисел, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Це стале для даної послідовності число q називають Знаменником геометричної прогресії. Формула n-го члена геометричної прогресії: . Теорема. Послідовність тоді й тільки тоді є геометричною […]...
- Послідовності Математика – Алгебра Послідовності Розглянемо яку-небудь множину, що містить дійсних чисел і кожний елемент якої відповідає одному з натуральних чисел від 1 до , або нескінченну множину дійсних чисел, кожному елементу якої можна поставити у відповідність натуральне число. Такі числа можна записати в певному порядку. Кажуть, що вони утворюють Послідовність. Наприклад: 2; 4; 6; 8; […]...
- Властивості додавання Розділ 4 Раціональні числа і дії мідними §40. Властивості додавання Для додавання раціональних чисел, як і для додавання додатних чисел, справджуються переставна і сполучна властивості. Переставна властивість додавання. Для будь-яких раціональних чисел а і b виконується рівність а + b = b + а. Перевіримо цю властивість на прикладах. Приклад 1. -8 + (-3) = […]...
- Генетичний код, його основні принципи і властивості МЕДИЧНА БІОЛОГІЯ Розділ 1 БІОЛОГІЧНІ ОСНОВИ ЖИТТЄДІЯЛЬНОСТІ ЛЮДИНИ 1.2. Молекулярно-генетичний і клітинний рівні організації життя 1.2.3. Спадковий апарат еукаріотичних клітин і його функціонування на молекулярному рівні 1.2.3.5. Генетичний код, його основні принципи і властивості Генетичний код ДНК. Унікальність кожної клітини полягає в унікальності її білків. Клітини, що виконують різні функції, здатні синтезувати свої власні білки, […]...
- Множення вектора на число Геометрія Вектори Множення вектора на число Добутком вектораНа число називається вектор , тобто . Для будь-якого вектора і чисел і . Для будь-яких двох векторів і і числа . Теорема 1. Абсолютна величина вектора дорівнює . Напрям вектора , якщо , збігається з напрямом вектора , якщо , і протилежний напряму вектора , якщо . […]...
- Основні властивості неперервних функцій Математика – Алгебра Границя Основні властивості неперервних функцій Теорема 1. Якщо функції і є неперервними в точці , то в цій точці будуть неперервними і функції , . Теорема 2. Якщо і є неперервними в точці і , то в точці є неперервною також і функція . Зверніть увагу: всі дробово-раціональні функції і основні тригонометричні […]...
- Властивості перетворення подібності Геометрія Подібність фігур Властивості перетворення подібності Теорема 1. Перетворення подібності переводить прямі у прямі, півпрямі – у півпрямі, відрізки – у відрізки. Теорема 2. Перетворення подібності зберігає кути між півпрямими. Із цього випливає, що перетворення подібності переводить паралельні прямі в паралельні прямі. Дві фігури називаються Подібними, якщо вони переводяться одна в одну перетворенням подібності. Позначення: […]...
- Переставна і сполучна властивості множення. Коефіцієнт буквеного виразу Розділ 4 Раціональні числа і дії мідними §44. Переставна і сполучна властивості множення. Коефіцієнт буквеного виразу Для множення раціональних чисел, як і для множення додатних чисел, справджуються переставна і сполучна властивості. Переставна властивість множення. – Для будь-яких раціональних чисел а і b виконується рівність ab = ba. Перевіримо цю властивість на прикладах. Приклад 1. -3 […]...
- Застосування похідної Математика – Алгебра Похідна Застосування похідної Нехай функція визначена на проміжку і . Функція називається Зростаючою в точці, якщо існує інтервал , де , який міститься у проміжку і є таким, що для всіх x з інтервалу і для всіх x з інтервалу . Функція називається Спадною в точці, якщо існує інтервал , який міститься […]...
- Властивості паралельних площин Геометрія Стереометрія Властивості паралельних площин Теорема 1. Якщо дві паралельні площини перетинаються третьою площиною (див. рисунок), то прямі перетину паралельні. На рисунку: ; . Теорема 2. Відрізки паралельних прямих, які містяться між двома паралельними площинами (див. рисунок), рівні. На рисунку: ; ; . Теорема 3. Нехай площини і паралельні (див. рисунок нижче) і є точка […]...
- Властивості подібних фігур Геометрія Подібність фігур Властивості подібних фігур Теорема. Коли фігура подібна фігурі , а фігура – фігурі , то фігури і Подібні. Із властивостей перетворення подібності випливає, що у подібних фігур відповідні кути рівні, а відповідні відрізки пропорційні. Наприклад, у подібних трикутниках ABC і : ; ; ; . Ознаки подібності трикутників Теорема 1. Якщо два […]...
- Показникова функція, її графік і властивості УРОК 43 Тема. Показникова функція, її графік і властивості Мета уроку. Засвоєння учнями поняття показникової функції, її властивостей і графіка. Обладнання. Таблиця “Показникова функція”. І. Аналіз контрольної роботи II. Повідомлення теми уроку III. Сприймання і усвідомлення нового матеріалу Функція виду у = ах, де а > 0, а? 1, називається показниковою (з основою а). Усне […]...
- Поняття первісної функції – Інтеграл і його застосування Математика – Алгебра Інтеграл і його застосування Поняття первісної функції Первісною для даної функції на заданому проміжку називається така функція , що для всіх . Операція знаходження первісної F для даної функції називається Інтегруванням. Теорема 1. Будь-яка неперервна на відрізку функція має первісну функцію. Лема. Якщо на деякому проміжку, то на цьому проміжку, де C […]...
- Рівносторонній трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівносторонній трикутник Якщо всі сторони трикутника рівні, він називається Рівностороннім. На рисунку . Теорема 1. У рівносторонньому трикутнику всі кути рівні. Теорема 2. У рівносторонньому трикутнику висота, медіана, бісектриса, проведені з однієї вершини, збігаються. Теорема 3. У рівносторонньому трикутнику всі медіани (висоти, бісектриси) рівні між собою....
- Числові та лінійні нерівності УРОК № 60 Тема. Числові та лінійні нерівності Тестові завдання 1. Яку подвійну нерівність задовольняє множина чисел, поданих на рисунку? А) -4 < x < 8; Б) -4 < х < 8; В) -4 < х < 8; Г) -4 < х < 8. 2. Відомо, що х < у. Яка з наведених нерівностей є […]...
- ВІДНОШЕННЯ ТА ЙОГО ВЛАСТИВОСТІ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ У розділі дізнаєтесь: Ü про відношення та його властивості; Ü що таке пропорція; Ü які є пропорційні залежності величин; Ü як поділити число в даному відношенні; Ü що таке масштаб; Ü про коло, круг, круговий сектор та просторові фігури обертання; Ü які є види діаграм та як будувати діаграми; Ü […]...
- ВЕЛИКІ ДОСЯГНЕННЯ МАЛИХ УКРАЇНЦІВ ЛЮДИНА ВЕЛИКІ ДОСЯГНЕННЯ МАЛИХ УКРАЇНЦІВ НАЙСИЛЬНІШИЙ ХЛОПЧИК СВІТУ Про цього хлопця точно не скажеш: “Мало каші їв”. Восьмирічний Єгор Леоненко із Сум зміг підняти штангу вагою 41 кілограм! Попередній світовий рекорд становив 40 кілограмів. Відтак Єгор здобув звання “Найсильніший хлопчик світу”. Єгор тренується по одній годині тричі на тиждень. А от зарядку робить щодня. Хобі […]...
- Теорема Вієта – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Теорема Вієта Щоб числа x1 та х2 були розв’язками рівняння ах2 + bх + с = 0, необхідно й достатньо, щоб:...