Властивості паралельних прямих
Урок № 8
Тема. Властивості паралельних прямих
Мета: домогтися засвоєння учнями змісту таких понять: “теорема”, “доведення теореми”, “умова і висновок теореми”, а також алгоритму доведення методом від супротивного; використовуючи метод доведення “від супротивного”, довести терему про дві прямі, паралельні третій.
Сформувати вміння:
– відтворювати означення основних понять уроку;
– застосовувати названі поняття під час розв’язування задач на паралельність.
Тип уроку: засвоєння знань, умінь
Наочність і обладнання: набір демонстраційного креслярського приладдя.
ХІД УРОКУ
І. Організаційний момент
ІІ. Перевірка домашнього завдання
Самоперевірка за зразком
Зразок виконання письмових вправ записаний на дошці заздалегідь.
Діти, не дивлячись у зошити, спочатку розглядають записане вчителем розв’язання, коментуючи його. По закінченні відкривають зошити і кожен, перевіряючи свою роботу, підкреслює помилки і виправляє їх.
ІІІ. Формулювання мети й завдань уроку. Мотивація навчальної діяльності
Для успішної мотивації діяльності учитель нагадує учням, що “геометрія
– означення;
– аксіоми;
– теореми.
На цьому уроці учні знайомляться з новим видом тверджень-теоремами.
Після попереднього етапу вчитель формулює мету та основне завдання уроку: ознайомитися із поняттям теореми та пов’язаними з ним поняттями.
IV. Актуалізація опорних знань
Запитання до класу
1. Які дві прямі площини називаються паралельними?
2. Що треба знати про дві прямі, щоб стверджувати, що вони паралельні?
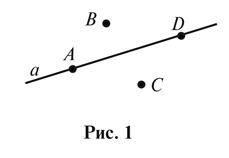
3. Через які з точок, зображених на рисунку 1, можна провести пряму, паралельну прямій a? Чому?
V. Засвоєння нових знань
План вивчення нового матеріалу
1°. Теорема: зміст поняття; умова й висновки теореми; доведення теореми.
2°. Доведення від супротивного.
3°. Теорема про дві прямі, паралельні третій (з доведенням методом від супротивного).
Методичний коментар
Оскільки на цьому уроці учні вперше знайомляться з поняттям “теорема”, необхідно детально пояснити учням не тільки відмінність теореми від аксiоми, але й пояснити, з чого складається теорема (умова й висновки), а також пояснити на нематематичних прикладах, що таке доведення (теореми).
Також учителю слід звернути увагу на те, що, на відміну від підручника О. В. Погорєлова, автори посібника вважають доречним ознайомлення учнів з методом доведення від супротивного із подальшим свідомим його застосуванням під час розв’язування задач.
VI. Первинне усвідомлення нового матеріалу
Виконання усних вправ
1. Відомо, що a||b, a||c. Про які ще прямі можна сказати, що вони паралельні?
2. Відомо, що a і b перетинаються, причому a||c. Чи може бути, щоб b||c?
3. Складіть твердження, протилежне даному:
А) прямі паралельні;
Б) пряма не може перетинати дві інші паралельні прямі в одній точці;
В) дві прямі проходять через одну точку.
Виконання графічних вправ
За допомогою двосторонньої лінійки проведіть паралельні прямі a і b.
А) Проведіть пряму c, паралельну прямій a. Чи паралельні прямі b і c? Чому?
Б) Позначте на прямій c точки A, B і C. Назвіть два промені, паралельні прямій b.
Виконання письмових вправ
1. Доведіть методом від супротивного твердження: “Якщо пряма паралельна одній зі сторін нерозгорнутого кута, то вона не може бути паралельною іншій його стороні”.
2. Пряма a паралельна прямій b і не паралельна прямій c. Доведіть, що прямі b і c перетинаються.
3 (на повторення). Накресліть кут AOB, що дорівнює 130°.
А) Поділіть його променем на два кути так, щоб один з них був більшим за інший на 32°;
Б) проведіть бісектрису кожного з утворених кутів та знайдіть кут між бісектрисами спочатку вимірюванням, а потім-виконавши обчислення. Порівняйте здобуті результати з градусною мірою даного кута. Що ви помітили?
VII. Підсумки уроку
Серед прямих a, b, c і d назвіть пряму, що не паралельна трьом іншим, якщо a||d, b і c перетинаються, c||d.
VIII. Домашнє завдання
Вивчити теоретичний матеріал уроку; повторити аксіоми вимірювання та відкладання кутів.
Письмово розв’язати задачі.
1. Три паралельні прямі перетинаються двома іншими паралельними прямими. Скільки точок перетину при цьому утворилося?
2. Прямі a і b перетинаються, пряма c паралельна прямій b. Доведіть, що будь-яка пряма, паралельна прямій a, перетинає прямі b і c.
3. Накресліть кут АВС, що дорівнює 70°.
А) Проведіть промінь BD, доповняльний до променя BC, і обчисліть утворений кут DBA;
Б) проведіть бісектрису BE утвореного кута і знайдіть кут DBE.
Джерела:
1. Уроки геометрії. 7 клас./ С. П. Бабенко – Х.: Вид. група “Основа”, 2007.- 208 с.