ВЛАСТИВОСТІ ПАРАЛЕЛЬНИХ ПРЯМИХ
РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ
& 7. ВЛАСТИВОСТІ ПАРАЛЕЛЬНИХ ПРЯМИХ
ЗАДАЧА
Дано пряму а і точку Р, що не належить цій прямій. Проведіть через точку Р пряму, паралельну прямій а.
– За допомогою лінійки і косинця побудову можна виконати, як показано на малюнку 90.
Чи можна через точку Р провести дві різні прямі, паралельні прямій а?
Геометри здавна вважали істинним таке твердження:
Через точку, яка не лежить на даній прямій, можна провести тільки одну пряму, паралельну даній.
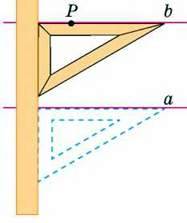
Мал. 90
Давньогрецький геометр Евклід це твердження прийняв без доведення. Його назвали аксіомою Евкліда, тому що всі твердження, які приймають без доведення, називають аксіомами. (Детальніше про аксіоми і теореми – у наступному параграфі.)
Не всі вчені аксіому Евкліда вважають правильною. Геометрію, у якій визнається правильною аксіома Евкліда, називають евклідовою геометрією. Ви вивчаєте евклідову геометрію.
Теорема 6 (обернена до теореми 3).
Якщо прямі паралельні, то внутрішні різносторонні кути, утворені ними з січною, – рівні.
Доведення Нехай прямі АВ і CD – паралельні, а КС –
Припустимо, що ∠CAB ≠ ∠ACD. Проведемо пряму АВ1 так, щоб виконувалась рівність ∠CAB, = ∠ACD. За ознакою паралельності прямих AB1 ‖ CD, а за умовою АВ ‖ CD. Виходить, що через точку А проведено дві різні прямі, паралельні прямій CD. Це суперечить аксіомі Евкліда. Отже, зроблене вище припущення призводить до суперечності. Тому ∠CAB = ∠ACD.
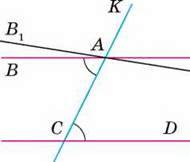
Мал. 91
Наслідок 1 Якщо прямі паралельні, то відповідні кути, утворені цими прямими з січною, – рівні.
Доведення Якщо а ‖ b, то за теоремою 6: ∠1 = ∠2 (мал. 92, a). ∠1 і ∠3 – вертикальні, тому ∠1 = ∠3. Оскільки ∠2 = ∠1, a ∠1 = ∠3, то ∠2 = ∠3.
Наслідок 2 Якщо прямі паралельні, то сума внутрішніх односторонніх кутів, утворених цими прямими з січною, дорівнює 180°.
Доведіть самостійно, використовуючи малюнок 92, б.

92, а

92, б
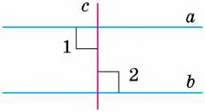
92, в
Наслідок 3 Якщо пряма перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до іншої прямої.
Справді, якщо с ⏊ а і а ‖ b, то ∠1 = ∠2 = 90°, тобто с ⏊ b (мал. 92, в).
Теорема 7 Дві прямі, паралельні третій, паралельні одна одній.
Доведення. Нехай кожна з прямих а і b паралельна прямій с. Доведемо, що а ‖b.
Припустимо, що прямі а і b не паралельні (мал. 93), а перетинаються в деякій точці Р. Виходить, що через точку Р проходять дві різні прямі а і b, паралельні прямій с. Це суперечить аксіомі Евкліда. Отже, прямі а і b не можуть перетинатися. Тоді вони паралельні.
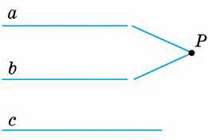
Мал. 93
Зверніть увагу! Доведення теореми правильне і для випадку, коли пряма с лежить між прямими а і b.
Для допитливих
1. Останню теорему називають теоремою про транзитивність паралельності прямих (лат. transitivus – перехідний), бо вона стверджує, що паралельність двох пар паралельних прямих переходить на третю пару: якщо а‖ b і b ‖ с, то а ‖ с.
Щоб це твердження виконувалося завжди, домовилися вважати, що кожна пряма паралельна сама собі, тобто а ‖ а. Адже
Якщо а ‖ b і b ‖ а, то а ‖ а.
2. Відрізки однієї прямої також вважають паралельними. Наприклад, якщо А, В, С, К – точки однієї прямої, то кожний з відрізків АВ, АС, АK, ВС, ВК, СК паралельний будь-якому з них (мал. 94). У доцільності такої домовленості ви переконаєтеся згодом, вивчаючи паралельне перенесення, паралельне проектування тощо. А в сьомому класі основна увага звертатиметься на паралельність відрізків і променів, що не лежать на одній прямій.
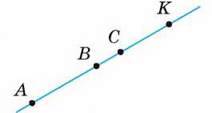
Мал. 94
3. Є геометрії, у яких аксіома Евкліда не вважається правильною. Їх називають неевклідовими геометріями. Такою, наприклад, є геометрія Лобачевського (див. с. 179).
Подане на с. 51 формулювання аксіоми Евкліда насправді належить грецькому математику Проклу Діадоху (V ст. н. е.), який сформулював її майже на 1000 років пізніше. Евклід же формулював цю аксіому інакше: “Якщо пряма, що падає на дві прямі, утворює внутрішні і по одну сторону кути, менші від двох прямих, то необмежено продовжені ці прямі зустрінуться з тієї сторони, де кути менші від двох прямих”.
Запитання і завдання для самоконтролю
1. Сформулюйте аксіому Евкліда про паралельність прямих.
2. Сформулюйте і доведіть теорему про внутрішні рівносторонні кути при паралельних прямих та січній.
3. Сформулюйте і доведіть властивості відповідних і внутрішніх односторонніх кутів при паралельних прямих і січних.
4. Сформулюйте і доведіть теорему про дві прямі, паралельні третій.
Виконаємо разом
1. Доведіть, що прямі, перпендикулярні до непаралельних прямих, перетинаються.
– Нехай прямі а і b перетинаються, а прямі m i n перпендикулярні до них: m ⏊ а, n ⏊ b (мал. 95).
Тоді ∠1 = ∠2 = 90°. Припустимо, що m ‖ n, тобто ∠1 = ∠3. Тоді й ∠2 = 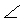 3, а звідси випливає, що а ‖b. Це суперечить умові задачі. Отже, прямі т і я не можуть бути паралельними. Тоді вони перетинаються.
3, а звідси випливає, що а ‖b. Це суперечить умові задачі. Отже, прямі т і я не можуть бути паралельними. Тоді вони перетинаються.
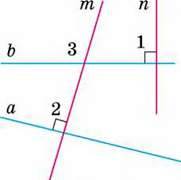
Мал. 95
ЗАДАЧІ І ВПРАВІ
Виконайте усно
194. Скільки пар паралельних прямих є на малюнку 96? А скільки пар непаралельних прямих?
195. Кут між прямими а і х дорівнює 70° (мал. 96). Знайдіть кути між усіма парами прямих, що є на малюнку.
196. Поясніть, як можна проводити паралельні прямі, користуючись рейсшиною (мал. 97).

Мал. 96
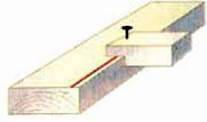
197. На малюнку 98 зображено саморобний рейсмус. Як таким рейсмусом можна проводити на бруску прямі, паралельні його ребрам?
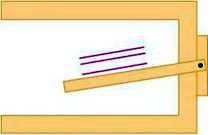
Мал. 97
Мал. 98
А
198. Міра одного з кутів, утворених двома паралельними прямими з їх січною, дорівнює 35°. Знайдіть міри інших кутів.
199. На стороні кута ABC взято точку А. Через неї проведено пряму, паралельну ВС. Знайдіть міри кутів при вершині А, якщо ∠ABC = 50°.
200. У прямокутнику АВСD ∠ВАС на 20° більший за ∠DAC. Знайдіть ∠ACB і ∠ACD.
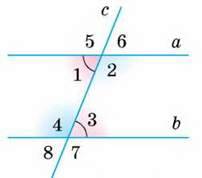
201. Знайдіть міри всіх кутів, зображених на малюнку 99, якщо а ‖ b і:
А) ∠1 = 60°;
Б) ∠5 + ∠7 = 250°;
В) ∠2 – ∠1 = 50°;
Г) ∠4 – ∠6 = 20°.
Мал. 99
202. Доведіть, що коли пряма перетинає одну з двох паралельних прямих, то вона перетинає й іншу пряму.
203. Прямі а і b не паралельні прямій с. Чи випливає з цього, що прямі а і b не паралельні?
204. Доведіть, що бісектриси двох відповідних кутів при паралельних прямих паралельні.
205. Доведіть, що коли одна січна з двома прямими утворює рівні відповідні кути, то й кожна інша січна з цими прямими утворює рівні відповідні кути.
206. Кут між однією з двох паралельних прямих і їх січною дорівнює 80°. Під яким кутом бісектриса цього кута перетинає іншу пряму?
207. На сторонах АВ і ВС трикутника ABC взято точки К і Р такі, що КР ‖ АС. Знайдіть кути чотирикутника АКРС, якщо ∠ВКР = 60°, ∠ВРК = 80°.
Б
208. Якщо прямі з січною утворюють нерівні відповідні кути, то вони перетинаються. Доведіть це.
209. Промені АВ, АС і KР різні і такі, що АВ ‖ КР, АС ‖ КР. Знайдіть міру кута ВАС.
210. Користуючись малюнком 99, на якому ∠1 = ∠3, обчисліть міри кутів 3 і 4, якщо:
А) ∠4 – ∠1 = 50°;
Б) ∠4 в 3 рази більший за ∠6.
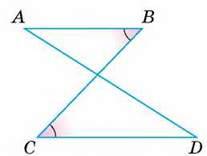
211. Сторони AD і ВС замкненої ламаної ABCDA перетинаються і ∠В = ∠С (мал. 100). Доведіть, що ∠A = ∠D.
Мал. 100
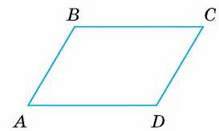
212. Кожна сторона чотирикутника ABCD паралельна протилежній стороні (мал. 101). Доведіть, що:
А) ∠А + ∠B = 180°;
Б) ∠B + ∠С = 180°;
В) ∠А = ∠С;
Г) ∠В = ∠D.
Мал. 101
213. У чотирикутнику ABCD ВС ‖ AD і ∠В = ∠С (мал. 102).
Доведіть, що:
А) ∠А = ∠D;
Б) ∠A + ∠С = 180°.
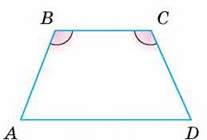
Мал. 102
214. Через точку, яка не лежить на прямій а, проведено три прямі. Доведіть, що принаймні дві з них перетинають пряму а.
215. Доведіть, що два кути з відповідно паралельними сторонами рівні або сума їх мір дорівнює 180°.
216. На малюнку 103 ∠1 = 70°, ∠2 = 50° і АВ ‖CD. Знайдіть міри кутів 3, 4 і 5.
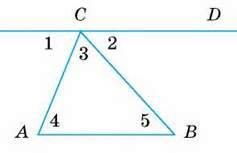
Мал. 103
217. На малюнку 104 ∠АВС = 50°, ∠CDE = 36°, АВ ‖DE. Знайдіть ∠BCD.
218. Одна насічка напилка утворює з його ребром кут 65°, а інша – 74° (мал. 105). Знайдіть міру гострого кута між двома різними насічками.
Мал. 104
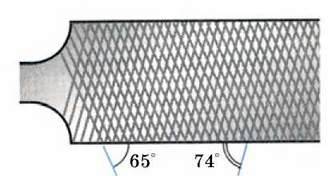
Мал. 105
Практичне завдання
219. Виміряйте необхідні кути (мал. 106) і встановіть, чи є паралельними червоні та сині лінії, які визначають елементи схеми для вишивання українського рушника.

Мал. 106
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
220. Знайдіть діаметр кола, якщо він довший за радіус:
А) на З см; б) на 3,5 м.
221. Чому дорівнює довжина кола, діаметр якого:
А) 10 см; б) 0,1 м?
222. Скільки спільних точок можуть мати:
А) пряма і коло;
Б) пряма і круг;
В) коло і коло?
223. Перемалюйте в зошит фігуру з малюнка 107. Як називають таку фігуру? Назвіть її вершини, ребра, грані.
224. Скільки різних пар паралельних ребер має куб?
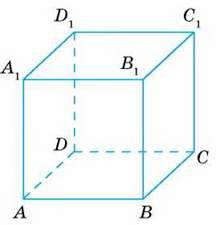
Мал. 107