Застосування векторів
269.
5(х – 2) + 0 × (у + 1) – 3(z – 4) = 0; 5x – 10 – Зz + 12 = 0;
5x – Зz + 2 = 0 – рівняння шуканої площини.
270.
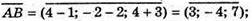
3(x – 1) – 4(y – 2) + 7(z + 3) = 0; 3x – 3 – 4у + 8 + 7z + 21 = 0;
3x – 4у + 7z + + 26 = 0 – рівняння даної площини.
271.
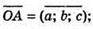 a(x -0) + b(y – 0) 4 – c(z – 0) = 0; ax + by + cz = 0
a(x -0) + b(y – 0) 4 – c(z – 0) = 0; ax + by + cz = 0
272.
Якщо площина α паралельна площині 2х – Зу + z + 10 = 0, то 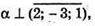
Тоді площина α задається рівнянням: 2(х – 1) – 3(у + 3) + 1(z – 5) = 0;
2х – 2 – Зy + 9 + z – 5 = 0; 2х – Зу + z – 16 = 0.
273.
Щоб
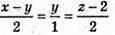 і
і 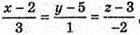
Достатньо знайти кут α між векторами 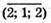 і
і 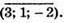
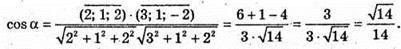
274.
Знайдемо кут між векторами 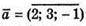 і
і 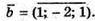
Цей кут дорівнюватиме куту між площинами.
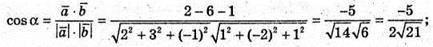
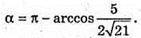
275.
Оскільки площина дотикається до сфери (х – 1)2 + (у + 1)2 + (z – 2)2 = 6
У точці (0; 0; 0), то дана площина перпендикулярна 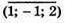 І проходить
І проходить
Через точку (0; 0; 0). Ця площина задається рівнянням:
1(х
276.
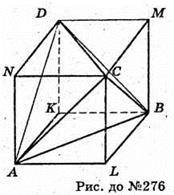
Добудуємо тетраедр ABCD до паралелепіпеда AKBLNDMC, провівши через протилежні ребра пари паралельних площин. За умовою AB + CD, тоді KL + AB, бо KL + DC. Звідси: у паралелограма AKBL діагоналі перпендикулярні, тому AKBL – ромб. Тоді АВ2 + KL2 =АВ2 + DC2 = а2 (а – сторона ромба).
Аналогічно AD2 + ВС2 = а2 і АС2 + BD2= а2 (всі грані паралелепіпеда – ромби). Звідси AD2 + ВС2 = АС2 + BD2 = АВ2 + DC2.
277.
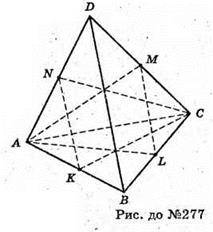
О – точка перетину медіан ΔАМL.
О1 – точка перетину медіан ΔCNK:
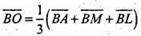
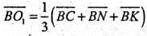
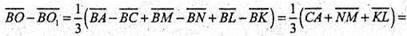
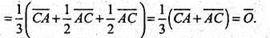
Оскільки 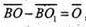 то
то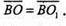
Отже, О і О1 збігаються.
278.
K – середина АА1; S – середина ВВ1; М – середина СС1;
N – середина DD1 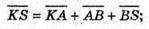
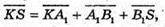
Звідси 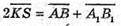 або
або 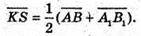
Аналогічно 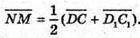
Оскільки AB? DC і А1 В1 ? D1 С1, то 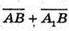 і
і 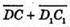
– колінеарні, тобто KS? NM, аналогічно SM? KN.
Звідси KSMN – паралелограм.
279.
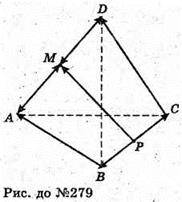
ABCDA – неплоска замкнена ламана.
М – середина AD; Р – середина ВС.
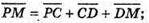
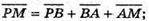
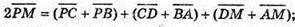
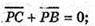
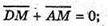
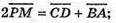
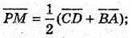
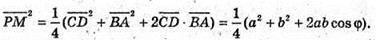
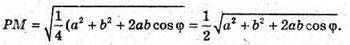
280.
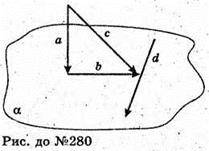
А + α; с – похила; b – проекція – на а.
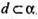 , d + b. Доведемо, що с + d.
, d + b. Доведемо, що с + d.
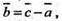 оскільки
оскільки 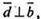 то
то 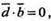
Тобто 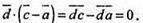
Оскільки 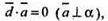 то
то 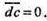
Тому 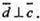
Якщо 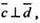 То і
То і 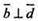 (доведення аналогічне:
(доведення аналогічне: 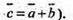
281.
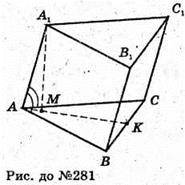
Опустимо A1M + (АВС).
Якщо ΔАВС – рівносторонній і ∠A1 AB = ∠А1АС, то М – основа перпендикуляра лежить на бісектрисі AK. АK – бісектриса, медіана і висота Δ АВС.
A1M + (ABC), тому A1M + ВС, тоді 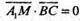
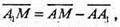 тоді
тоді 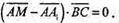
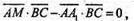 Оскільки
Оскільки 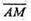 лежить на
лежить на 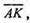
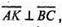 бо
бо 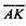 – висота ΔАВС.
– висота ΔАВС.
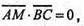 Тоді
Тоді 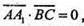 тому
тому 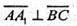
Або 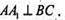
282.
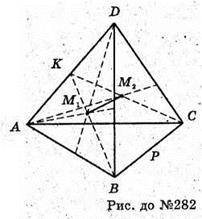
ABCD – тетраедр.
Μ1 – точка перетину медіан ΔABD. М2 – точка перетину медіан Δ ACD.
ВK – медіана ΔABD: 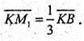
СK – медіана ΔACD: 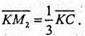
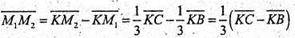
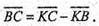 Звідси
Звідси 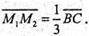
Отже,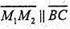 або М1М2 ? ВС.
або М1М2 ? ВС.
283.
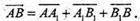
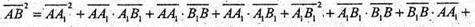
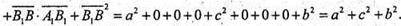
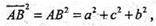 тоді
тоді 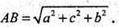
284.
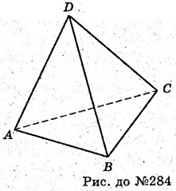
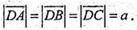
∠ ADB = ∠DBC = ∠CDA = β.
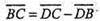
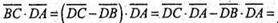
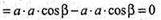
Отже, 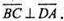
Отже, ребро тетраедра перпендикулярне до протилежного.
285.
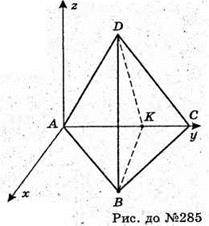
Розмістимо тетраедр в системі координат як показано на рисунку.
А – ребро тетраедра.
Тоді A(0; 0; 0); 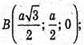
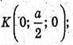
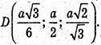
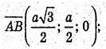
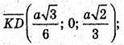
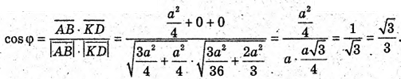
Отже, 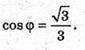
286.
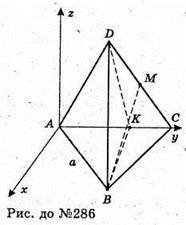
А – ребро тетраедра. DK + ВМ – мимобіжні медіани граней тетраедра,
φ – кут між ними.
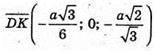 (див. задачу № 285).
(див. задачу № 285).
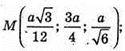
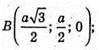
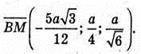
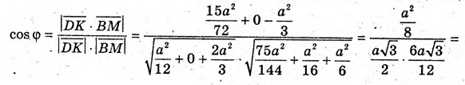
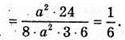
Отже, 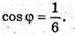
287.
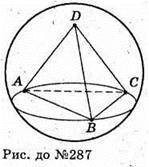
О – центроїд тетраедра. М – довільна точка сфери.
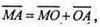
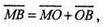
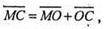
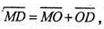
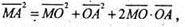
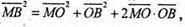
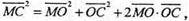
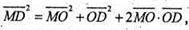
Тоді
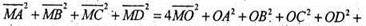
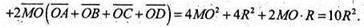
288.
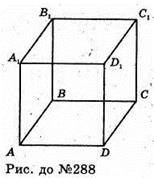
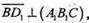 тому
тому 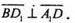
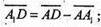
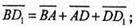
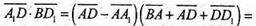
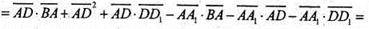
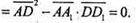
Звідси 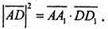
Оскільки 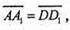 то
то 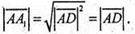
Аналогічно можна довести, що 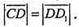
Тому AD = DD1 = DC.
Отже, AВСDA1В1С1D1 – куб.
289.
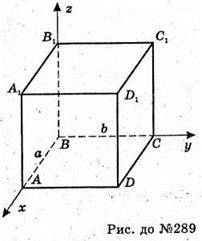
Нехай а, b, с – виміри прямокутного паралелепіпеда.
Розмістимо паралелепіпед в системі координат, як показано на рисунку.
Тоді А(а; 0; 0); В(0; 0; 0); С(0; 6; 0); D(a; b; 0);
А1(A; 0; с); В1 (0; 0; с); С1 (0; b; с); D1(а; b; с).
O(х; у; z) – довільна точка простору.
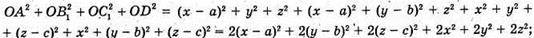
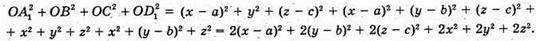
Звідси: 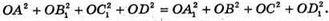
290.
Пряма АВ: 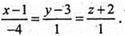
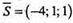 :- площина.
:- площина.
Х + 2у – z + 3 = 0, 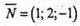
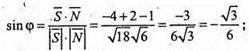

291.
А) Множина точок, рівновіддалених від площин 2х – у + Зz – 5 = 0 і 2х – y + 3z + 3=0 утворюють площину, паралельну даним площинам, яка проходить між даними площинами на однаковій відстані. Ця площина задається рівнянням 2х – у + Зz – 1= 0.
Б) Множина точок, рівновіддалених від площин 2х + у – 2z + 5 = 0 і х – 2у + 2z – 1 = 0 утворює бісекторну площину для даних площин і задається рівнянням:
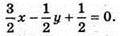
292.

AD1 і BC1 – мимобіжні діагоналі суміжних граней куба; а – ребро куба.
Проведемо через AD1 і DC1 площини, паралельні між собою.
Це (AB1D1) і (C1BD). Ці площини перпендикулярні до діагоналі А1С
І ділять її на три рівні частини.
Відстань між площинами d дорівнює 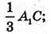
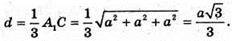
293.
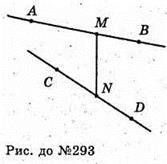
Нехай М? AB, N? CD i MN – відстань між АВ і CD.
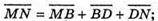
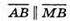 і
і 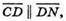
Тому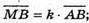
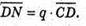
Звідси 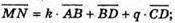
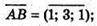
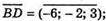
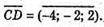
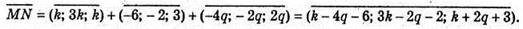
Оскільки 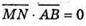 і
і 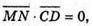 бо
бо 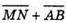 і
і 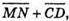
То
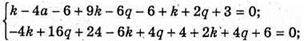
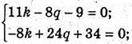
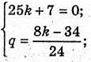
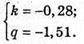
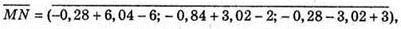
Тоді 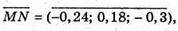
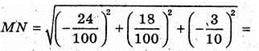
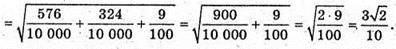
294.
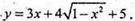
Введемо вектори 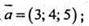
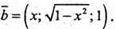
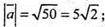
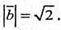
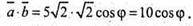
Найбільшого значення 10 функція набуває, коли
Cos φ = 1, тобто φ = 0°, тоді а і b співспрямовані.
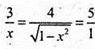 або
або 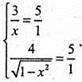
Звідси 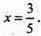
Отже, найбільше значення функції дорівнює 10 і досягається при