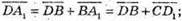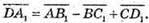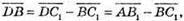Алгебра векторів
1.
 Побудуємо вектори
Побудуємо вектори 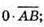
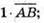
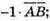
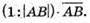
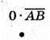
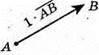
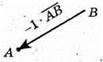
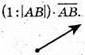 – одиничний вектор
– одиничний вектор
2.
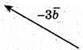
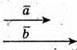 Побудуємо вектори
Побудуємо вектори 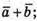
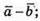
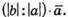
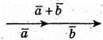
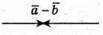
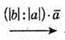
3.
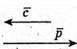 Побудуємо вектори
Побудуємо вектори 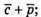
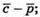
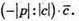
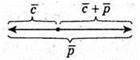
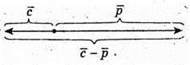
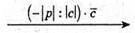
4.
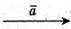
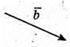
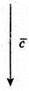 Побудуємо вектори
Побудуємо вектори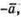
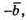
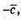
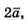
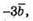
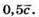
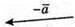
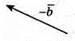

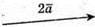
5.

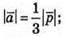
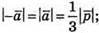
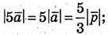
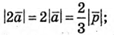
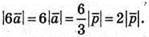
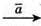
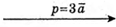
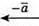
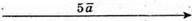
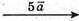
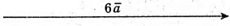
6.
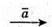
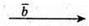
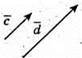
1) Побудуємо вектори 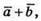
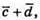
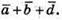
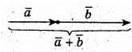
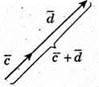
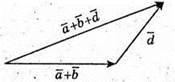
2) Побудуємо вектори 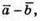
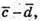
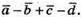
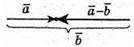
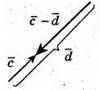
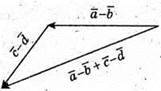
7.
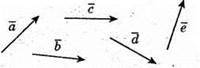 Побудуємо вектори
Побудуємо вектори 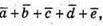
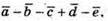
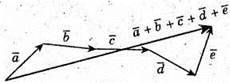
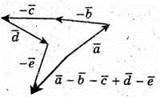
8.
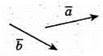
1) 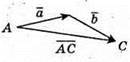 2)
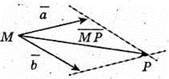
2) 
9.
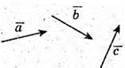 Побудуємо вектори
Побудуємо вектори 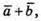
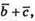
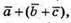
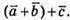
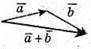
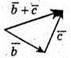
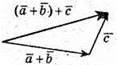
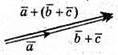
Вектори 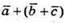 та
та 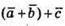 рівні.
рівні.
10.
Накреслимо два ненульові вектори 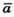
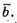
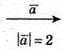
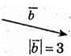
Побудуємо 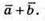
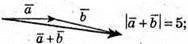
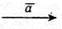
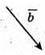
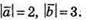
Побудуємо 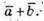
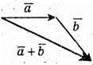
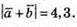 Таким чином,
Таким чином, 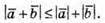
11.
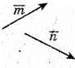 Побудуємо вектори
Побудуємо вектори 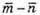
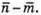
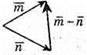
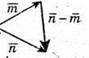
Вектори 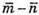
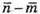 протилежно напрямлені.
протилежно напрямлені.
12.
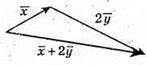
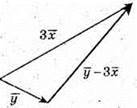
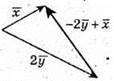
 Побудуємо вектори
Побудуємо вектори 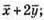
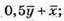
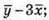
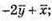
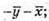
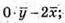
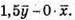
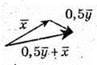
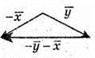
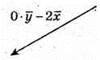
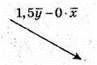
13.
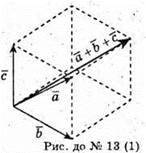
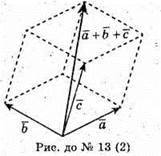
1) Побудуємо паралелепіпед на векторах 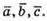
Його діагональ – це вектор 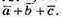
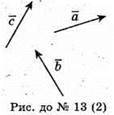
2) Сумістимо вектори та побудуємо на них паралелограм,
Його діагональ – це сума векторів.
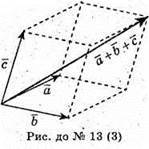
3) Сумістимо вектори та побудуємо на них паралелепіпед,
Його діагональ – це сума векторів.
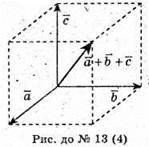
4) Сумістимо вектори та побудуємо на них паралелограм,
Його діагональ – це сума векторів.
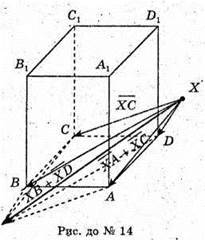
14.
Отримані вектори рівні.
15.
1)Так, може. Якщо 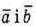 – довільні неколінеарні вектори або колінеарні однаково напрямлені ненульові вектори.
– довільні неколінеарні вектори або колінеарні однаково напрямлені ненульові вектори.
2) Так, може. Якщо 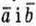 – довільні колінеарні протилежно напрямлені.
– довільні колінеарні протилежно напрямлені.
3) Ні, не може.
16.
1) 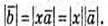 Якщо
Якщо 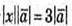 і вектори співнапрямлені, то х = 3.
і вектори співнапрямлені, то х = 3.
2) 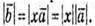 Якщо
Якщо  і вектори протилежно напрямлені, то х = -3.
і вектори протилежно напрямлені, то х = -3.
17.
1) Щоб вектори були рівними, повинні виконуватися умови:
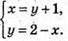
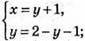
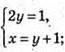
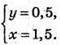
Вектори рівні, якщо х = 1,5 і у = 0,5.
2) Щоб вектори були рівними, повинні виконуватися умови: 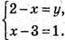
Розв’яжемо систему: 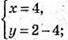
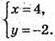
Вектори рівні, якщо х = 4 і у = -2.
18.
1) Щоб вектори були колінеарні, повинні виконуватися умови:
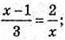 х2 – x = 6; х2 – x – 6 = 0; x1 = 3, х2 = -2.
х2 – x = 6; х2 – x – 6 = 0; x1 = 3, х2 = -2.
2) Щоб вектори були співнапрямлені, повинні виконуватися умови:
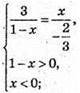
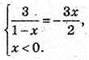
Розв’яжемо рівняння: 6 = – Зх(1 – x);
6 = -3х + 3×2; 3×2 – Зх – 6 = 0; х2 – х – 2 = 0: х1 = 2, х2 = -1;
Х = 2 – не задовольняє умові х < 0,
Отже, при х – -1 вектори співнапрямлені.
19.
Оскільки виконується рівність  то
то 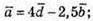
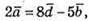
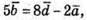
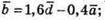
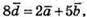
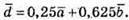
Вектор 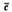 не можна подати у вигляді лінійної комбінації інших векторів,
не можна подати у вигляді лінійної комбінації інших векторів,
Оскільки задані вектори компланарні.
20.
1) Вектори є компланарними. 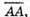
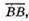
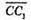
2) Вектори не є компланарними. 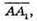
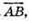
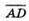
3) Вектори є компланарними. 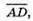
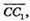
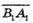
4) Вектори є компланарними. 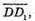
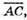
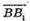
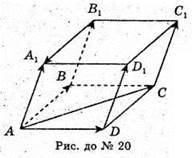
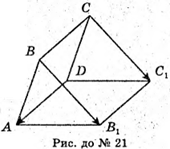
21.
Оскільки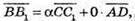 то вектори компланарні.
то вектори компланарні.
22.
1) 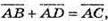
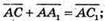
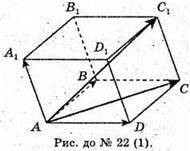
2) 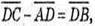
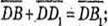
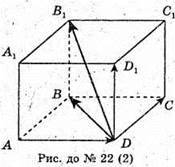
3) 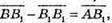
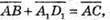
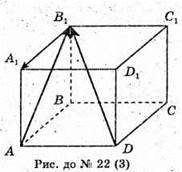
4) 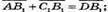
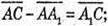
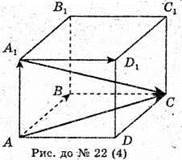
5) 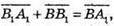
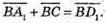
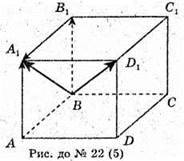
23.
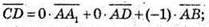
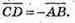
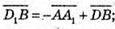
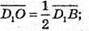
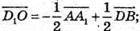
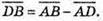 Тоді
Тоді 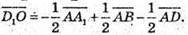
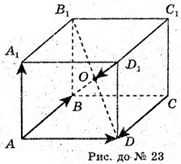
24.
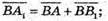
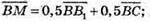
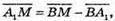
Тоді 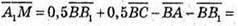
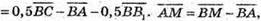
Тоді 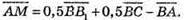
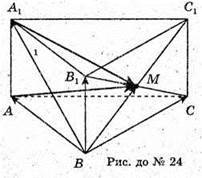
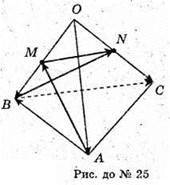
25.
Розкладемо вектор 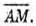
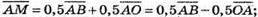
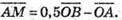 тоді
тоді 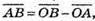
Розкладемо вектор 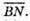
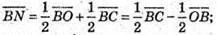
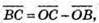 тоді
тоді 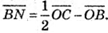
Розкладемо вектор 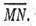
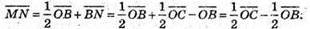
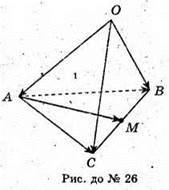
26.
Розкладемо вектор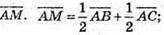 Тоді
Тоді 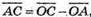
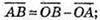
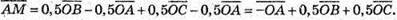
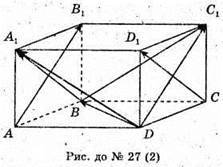
27.
1) 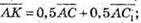
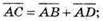
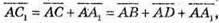
Тоді 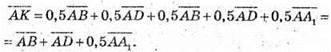
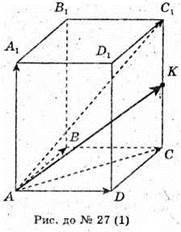
2)