Додавання векторів
УРОК № 44
Тема. Додавання векторів
Мета уроку: формування вміння додавати вектори, вивчення властивостей суми векторів; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13].
Вимоги до рівня підготовки учнів: описують додавання векторів; відкладають вектор, що дорівнює сумі векторів; формулюють властивості суми векторів; застосовують вивчені властивості й означення до розв’язування
Хід уроку
І. Перевірка домашнього завдання
Перевірити наявність виконаних домашніх завдань за записами, зробленими на дошці до початку уроку, та відповісти на запитання, які виникли в учнів під час виконання домашніх завдань.
Фронтальна бесіда
1) Що таке координати вектора? 2) Чому дорівнює абсолютна величина вектора з координатами а1, а2? 3) Які координати мають рівні вектори? протилежні вектори? 4) Знайдіть довжину вектора 
(-3; 4).
II. Поетапне сприймання й усвідомлення нового матеріалу
Додавання векторів
Сумою двох векторів
називається третій вектор с, початок якого збігається з початком , а кінець – з кінцем вектора при умові, що кінець вектора збігався з початком вектора (рис. 198).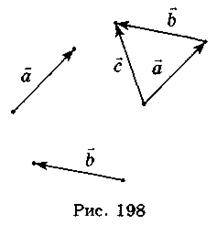
Це правило додавання векторів називається правилом трикутника. Колінеарні вектори також додаються за цим правилом (рис. 199).
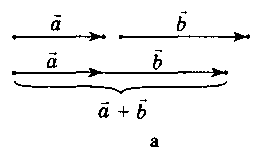
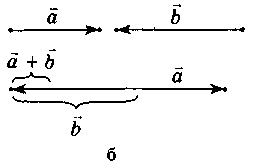
Рис. 199
Правило додавання векторів можна сформулювати і в іншій формі: для будь-яких трьох точок А, В, С має місце рівність 
+ 
= 
.
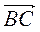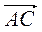Основні властивості додавання векторів
1) + = + (переставний закон додавання);
2) ( + ) + 
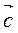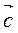= + ( + ) (сполучний закон додавання);
3) + 0 = (закон додавання вектора до нульового вектора);
4) + (-) = 0 (закон додавання протилежних векторів).
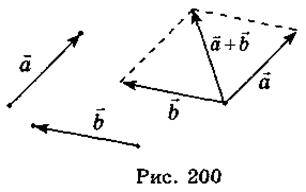
Властивість 1 дозволяє виконувати додавання векторів за правилом паралелограма (рис. 200): відкласти два вектори від однієї точки, тоді вектор суми цих векторів буде збігатися з діагоналлю паралелограма, який побудовано на даних векторах.
Координати суми двох векторів дорівнюють сумі відповідних координат даних векторів. Якщо (а1; а2) і (b1; b2) і 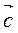= + , то 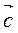(a1 + b1; a2 + b2).
Виконання вправ
1) Знайдіть вектор 
, який дорівнює сумі векторів і , та абсолютну величину вектора , якщо:
А) (5; 7) і (1; 1);
Б) (10; 10) і (-5; 2).
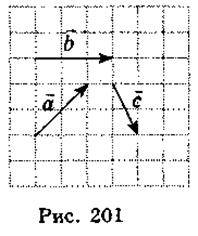
2) Накресліть у зошитах вектори , , так, як показано на рис. 201. Побудуйте вектор, який дорівнює:
А) + ;
Б) + ;
В) + + .
ІІІ. Закріплення та осмислення нового матеріалу
Розв’язування задач
1. На рис. 202 зображено паралелограм ABCD. Запишіть вектор, який дорівнює сумі векторів:
А) + ;
Б) + 
;
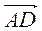В)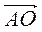 
+ 
;
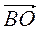Г) +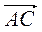 
.
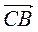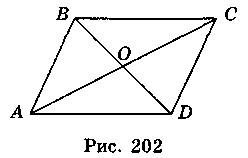
2. Спростіть вираз:
А) + 
+ + 
+ 
+ 
;
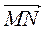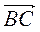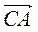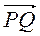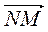Б)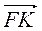 
+ 
+ 
+ 
+ 
+ 
.
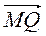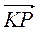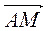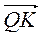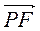3. О – центр правильного шестикутника ABCDEF. Доведіть, що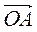 
+ 
+ 
+ 
+ 
+ 
= 
.
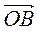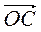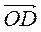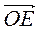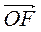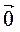IV. Домашнє завдання
1. Вивчити теоретичний матеріал. 2. Розв’язати задачі. 1) Спростіть вираз:
A)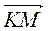 
+ 
+ + + 
+ + 
;
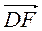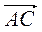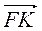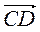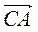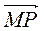Б) + 
+ + + 
+ .
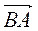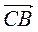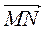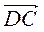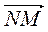2) О – точка перетину діагоналей паралелограма ABCD. Доведіть, що + + + = .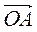
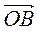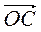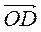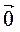V. Підбиття підсумків уроку
Заповніть пропуски в тексті.
Щоб побудувати вектор , що дорівнює + , треба від кінця вектора відкласти вектор , потім вектор , початок якого збігається з початком вектора…, а кінець – з кінцем вектора… (правило трикутника). Для векторів і зі спільним початком їхня сума зображається… паралелограма, який побудовано на цих векторах (правило паралелограма). Які б не були точки А, В, С, має місце векторна рівність + 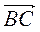= …. Сума протилежних векторів дорівнює… . Якщо сума двох векторів дорівнює 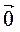, то ці вектори… .
(1 votes, average: 5.00 out of 5)
Loading...