Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Колінеарні вектори

Колінеарні вектори

УРОК № 48

Тема. Колінеарні вектори

Мета уроку: формування поняття “колінеарні вектори”; вивчення властивості та ознаки колінеарних векторів; формування вмінь учнів застосовувати вивчені означення та властивості до розв’язування завдань.

Тип уроку: комбінований.

Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13].

Вимоги до рівня підготовки учнів: описують колінеарність векторів; застосовують вивчені означення та властивості до розв’язування задач.

Хід уроку

I. Перевірка

домашнього завдання

Правильність виконання домашніх завдань перевірити за записами на дошці, які зроблено до початку уроку.

Математичний диктант

Дано вектори:

Варіант 1

(3; 0); (7; 4)

Варіант 2

(-2; 2); (1; 6)

Запишіть:

А) координати вектора + ;

Б) координати вектора – ;

В) координати вектора – ;

Г) довжину вектора

–

;

Д) координати вектора 2 – ;

Є) довжину вектора 2 – .

II. Сприймання й усвідомлення нового матеріалу

Якщо вектори колінеарні, то їхні відповідні координати пропорційні. І навпаки, якщо відповідні координати двох векторів пропорційні, то ці вектори колінеарні.

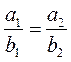Якщо вектори (a1; a2) і (b1; b2) колінеарні, то . Якщо 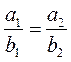і (a1; a2), (b1; b2), то вектори і колінеарні.

Колективне виконання вправ

1) Серед векторів (-2; 4), (2; 2), (0; -1), 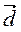(1; -2) знайдіть колінеарні.

Розв’язування

Оскільки вектори колінеарні, якщо їхні відповідні координати пропорційні, то маємо 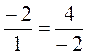= -2, звідси вектори i 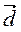колінеарні.

Відповідь: i .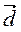

2) Знайдіть довжину вектора (6; у), якщо він колінеарний вектору + , де (-2; 0), (0; 1).

Розв’язання

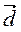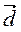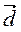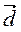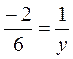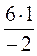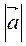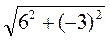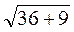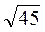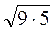Нехай + = , тоді (-2 + 0; 0 + 1) = (-2; 1). Оскільки вектори і колінеарні, то , звідси у = = -3, тоді (6; -3) і = = = = = 3.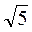

Відповідь: 3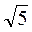

Самостійне виконання вправ

1) Визначте, чи колінеарні вектори:

А) (2; 3) і (-4; 6);

Б) (1; 3) і (-3; -9).

2) При якому значенні m вектори (15; m) і (18; 12) колінеарні? 3) Чи колінеарні вектори і 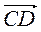, якщо А(3; -2), B(-1; 4), C(1; 3), D(-3; 9)? 4) При якому значенні n вектори і 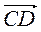колінеарні, якщо А(1; 0), В(3; n), С(2; 2), D(5; 4)?

III. Самостійна робота

Самостійну роботу навчального характеру можна провести за посібником [14], тест 15 “Векторні величини. Дії над векторами”.

IV. Домашнє завдання

1. Вивчити теоретичний матеріал. 2. Розв’язати задачі. 1) Відомо, що вектори (1; -1) і (-2; m) колінеарні. Знайдіть m. 2) Серед векторів 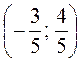, , 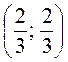(0; 1), 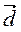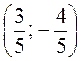знайдіть одиничні і зазначте, які з них колінеарні.