Координати вектора. Дії над векторами, що задані координатами
1.
Запишемо координати вектора:
1) 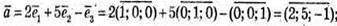
2) 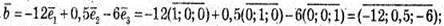
3) 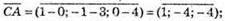
4) 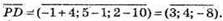
2.
1) 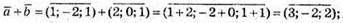
2) 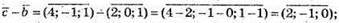
3) 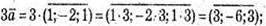
4) 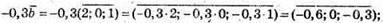
5) 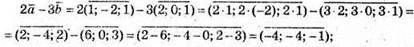
6) 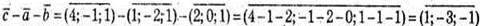
3.
1) 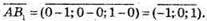
Запишемо розклад за координатними векторами: 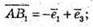
2) 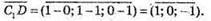
Запишемо розклад за координатними векторами: 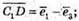
3) 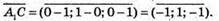
Запишемо розклад за координатними векторами: 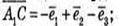
4) Знайдемо координати векторів 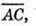
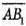 :
:
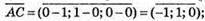
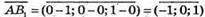
Знайдемо координати вектора 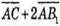
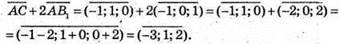
Запишемо розклад за координатними векторами: 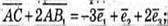
5) Знайдемо координати векторів 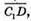
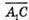
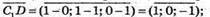
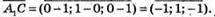
Знайдемо координати вектора 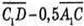
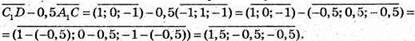
Запишемо розклад за координатними векторами: 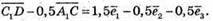
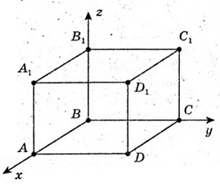
4.
1) Знайдемо координати вектора 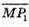
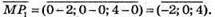
Запишемо розклад вектора за координатними векторами: 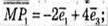
2) Знайдемо координати вектора 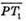
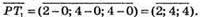
Запишемо розклад вектора за координатними векторами: 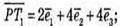
3) Знайдемо координати вектора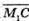

Запишемо розклад вектора за координатними векторами: 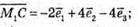
4) Знайдемо координати векторів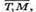
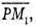
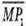
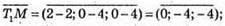
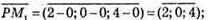
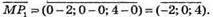
Знайдемо координати вектора 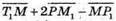
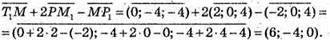
Запишемо розклад вектора за координатними векторами:
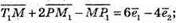
5) Знайдемо координати векторів 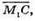
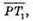
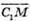
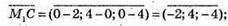
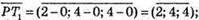
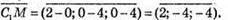
Знайдемо координати вектора 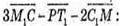
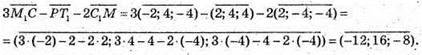
Запишемо розклад вектора за координатними векторами:
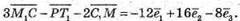
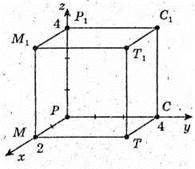
5.
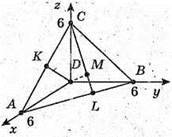
1) Розглянемо трикутник ADC – прямокутний 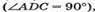 Рівнобедрений.
Рівнобедрений.
DK – висота, а оскільки трикутник рівнобедрений, то DK є медіаною.
Знайдемо координати точки К – середини відрізка АС: 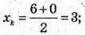
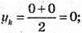
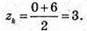
Знайдемо координати вектора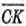
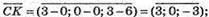
2) Основою піраміди є правильний трикутник ABC.
AD = BD = CD. Точка M є центром правильного трикутника ABC.
Скористаємось тим, що М – точка перетину медіан, а медіани точкою перетину діляться у відношенні 2 : 1.
Знайдемо координати точки L – середини відрізка АВ:
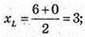
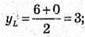
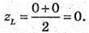
Знайдемо координати точки М: 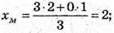
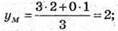
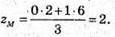
Знайдемо координати вектора 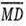
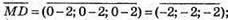
3) DM – висота піраміди, DM перпендикулярна до площини ARC.
Отже вектор 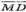 перпендикулярний До площини трикутника.
перпендикулярний До площини трикутника.
Знайдемо координати вектора 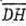
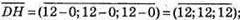
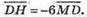
Отже вектор 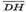 Перпендикулярний площині ABC, а отже пряма,
Перпендикулярний площині ABC, а отже пряма,
Проходить через точки D i Н перпендикулярна площині ABC.
6.
1) Знайдемо довжину вектора 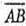
 Координати вектора.
Координати вектора. 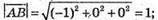
2) Знайдемо довжину вектора 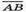
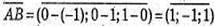 координати вектора.
координати вектора.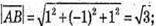
3) Знайдемо довжину вектора 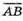
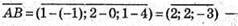 координати вектора.
координати вектора. 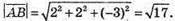
7.
1) Знайдемо 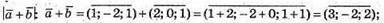
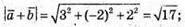
2) Знайдемо 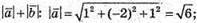
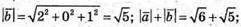
3) Знайдемо 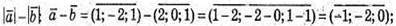
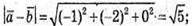
4) Знайдемо 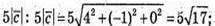
5) Знайдемо 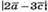
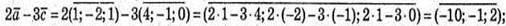
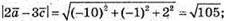
6) Знайдемо 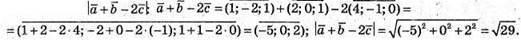
8.
З’ясуємо, при якому значенні п довжина вектора буде дорівнювати 1.
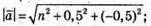
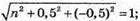 n2 + 0,25 + 0,25 = 1; n2 = 0,5;
n2 + 0,25 + 0,25 = 1; n2 = 0,5; 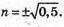
За умовами задачі 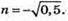
9.
Знайдемо довжину вектора 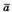
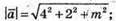
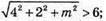 16 + 4 + m2 > 36; m2 > 16.
16 + 4 + m2 > 36; m2 > 16.
Оскільки треба знайти натуральне значення, то m > 4.
Найменше натуральне m = 5, при якому довжина вектора
Буде більша за число 6.
10.
Знайдемо довжину вектора 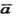
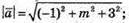
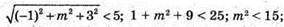
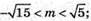
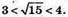
M = 3 – найбільше натуральне значення m, при якому довжина
Вектора буде менша за число 5.
11.
Щоб перевірити колінеарність, перевіримо пропорційність відповідних координат.
1) 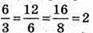 – вектори колінеарні;
– вектори колінеарні;
2) 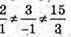 – вектори не колінеарні;
– вектори не колінеарні;
3) 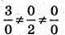 – вектори не колінеарні;
– вектори не колінеарні;
4) 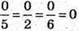 – вектори колінеарні;
– вектори колінеарні;
5)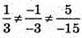 – вектори не колінеарні.
– вектори не колінеарні.
12.
Задані вектори колінеарні за умови пропорційності їхніх координат:
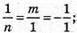
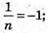 n = -1; m = -1.
n = -1; m = -1.
13.
1) Вектори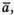
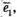
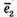 компланарні, оскільки
компланарні, оскільки 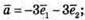
2) Вектори 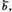
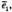
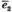 не компланарні, оскільки не існує таких чисел m і n,
не компланарні, оскільки не існує таких чисел m і n,
Щоб 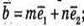
3) Вектори 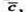
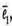
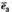 компланарні, оскільки
компланарні, оскільки 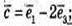
4) З’ясуємо чи існують такі числа m і n, щоб 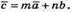
Запишемо рівність через координати векторів:
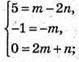
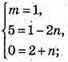
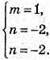 Вектори компланарні,
Вектори компланарні,
5) З’ясуємо чи існують такі числа m і n, щоб 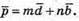
Запишемо рівність через координати векторів:
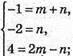
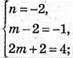
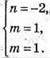
Вектори компланарні.
6) З’ясуємо чи існують такі числа m і n, щоб 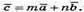
Запишемо рівність через координати векторів:
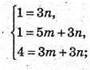
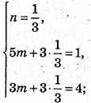
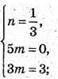
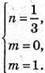
Вектори не є компланарними.
14.
1) Знайдемо 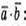
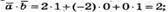
2) Знайдемо 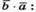
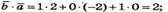
3) Знайдемо 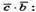
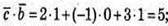
4) Знайдемо 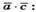
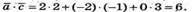
15.
Знайдемо скалярний добуток векторів 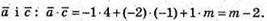
1) З’ясуємо при якому m він дорівнює 1; m – 2 = 1; m = 3;
2) З’ясуємо при якому m він дорівнює 2: m – 2 = 2; m = 4;
3) З’ясуємо при якому m він дорівнює 0: m – 2 = 0; m = 2;
4) З’ясуємо при якому m він дорівнює -1: m – 2 = -1; m = 1.
16.
1) 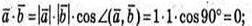
2) 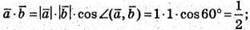
3) 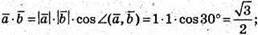
4) 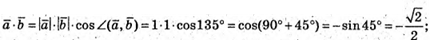
5) 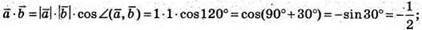
6) 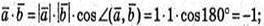
7) 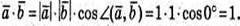
17.
Знайдемо скалярні добутки 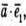
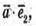
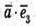
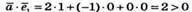 – отже вектор
– отже вектор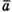 з віссю Ох утворює гострий кут;
з віссю Ох утворює гострий кут;
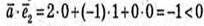 – отже вектор
– отже вектор 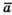 з віссю Oу утворює тупий кут;
з віссю Oу утворює тупий кут;
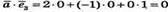 – отже вектор
– отже вектор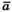 перпендикулярний до осі Oz.
перпендикулярний до осі Oz.
18.
1) З’ясуємо при якому значенні n вектори будуть перпендикулярні, тобто їх
Скалярний добуток буде дорівнювати 0.
-1 × 1 + 2n × (-1) + 0 × 2 = 0; 1 – 2 = 0; 2n = -1; n = -0,5;
2) Задані вектори колінеарні за умови пропорційності
Їхніх координат: 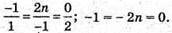
Такого значення n, при якому вектори будуть колінеарні не існує.
3) З’ясуємо, чи існують такі значення m і р, при яких 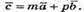
Запишемо рівність через координати:
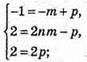
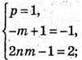
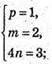
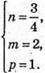
При 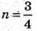 вектори будуть компланарні.
вектори будуть компланарні.
19.
З’ясуємо при якому значенні m вектори будуть перпендикулярні, тобто
При якому m > 0 скалярний добуток буде дорівнювати 0:
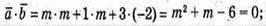 m = -3, m = 2.
m = -3, m = 2.
Оскільки за умовами m > 0, то при m = 2 вектори перпендикулярні.
20.
З’ясуємо при якому значенні m < 0 вектори будуть перпендикулярні,
Тобто при якому m < 0 скалярний добуток буде дорівнювати 0.
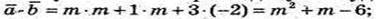 m2 + m – 6 = 0; m = -3, m = 2.
m2 + m – 6 = 0; m = -3, m = 2.
Оскільки за умовами m < 0, то при m = -3 вектори перпендикулярні.
21.
1) Знайдемо косинус кута між векторами 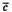 i
i 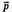
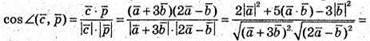
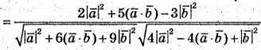
Оскільки 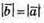 Та
Та 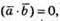 маємо
маємо
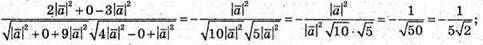
2) Знайдемо косинус кута між векторами 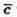 i
i 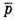
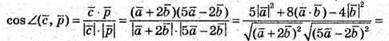
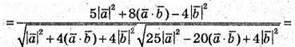
Оскільки 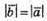 та
та 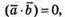 маємо
маємо
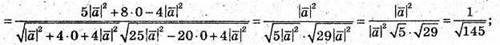
3) Знайдемо косинус кута між векторами 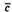 i
i 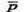
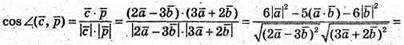
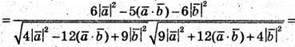
Оскільки 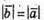 та
та 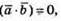 маємо = 0. Отже вектори
маємо = 0. Отже вектори 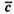 i
i 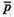 перпендикулярні.
перпендикулярні.
4) Знайдемо косинус кута між векторами 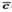 i
i 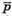
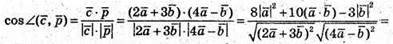
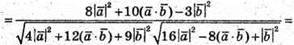
Оскільки 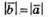 та
та 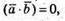 маємо
маємо
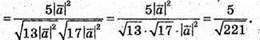
22.
1) З’ясуємо при якому значенні n вектори 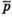 і
і 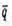 перпендикулярні,
перпендикулярні,
Тобто при якому n скалярний добуток дорівнює 0.
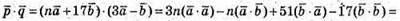
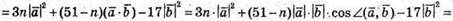
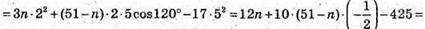
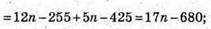
17n – 680 = 0; 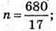 n = 40;
n = 40;
2) З’ясуємо при якому значенні n вектори 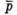 І
І 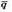 перпендикулярні,
перпендикулярні,
Тобто при якому n скалярний добуток дорівнює 0.
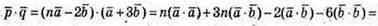
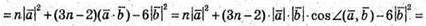
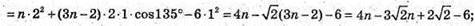
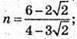
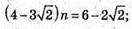
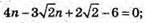
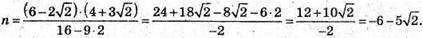
23.
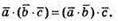
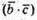 та
та 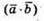 – числа, тому рівність буде виконуватися,
– числа, тому рівність буде виконуватися,
Якщо вектори 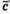 і
і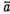 колінеарні і ненульові.
колінеарні і ненульові.
24.
Розглянемо скалярні добутки:
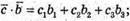
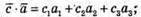
С1b1 + с2b2 + с3b3 = с1a1 + с2a2 + с3a3 значить, b1 = a1, b2 = a2, b3 = а3, тобто 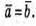
25.
Знайдемо кут між векторами 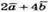 і
і 
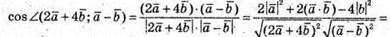
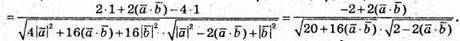
Обчислимо 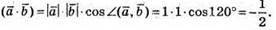
Тоді 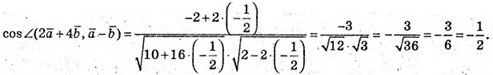
Кут між векторами дорівнює 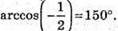
26.
Знайдемо скалярний добуток векторів 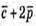 і
і 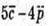
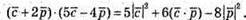
Оскільки вектори рівні 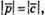 тоді
тоді 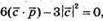 оскільки вектори перпендикулярні
оскільки вектори перпендикулярні
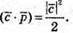
Знайдемо кут між векторами 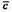 і
і 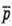
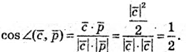
Отже кут між векторами 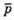 і
і 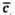 дорівнює 60°.
дорівнює 60°.
27.
Знайдемо кут між векторами 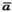 і
і 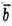
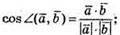
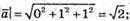
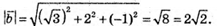
Знайдемо скалярний добуток 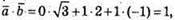
Тоді 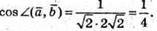 Куτ гострий.
Куτ гострий.
З основної тригонометричної тотожності 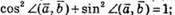
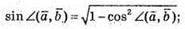
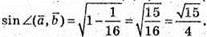
Площу паралелограма обчислимо за формулою
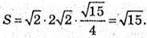
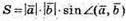
2) Знайдемо кут між векторами 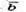 і
і 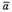
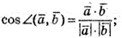
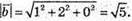
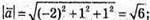
Знайдемо скалярний добуток 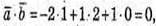 вектори перпендикулярні.
вектори перпендикулярні.
Обчислимо площу за формулою 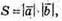
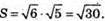
28.
Розглянемо скалярний квадрат
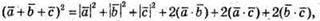
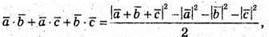
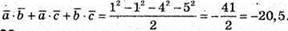
29.
Розглянемо скалярний квадрат
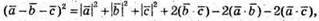
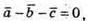
Отже 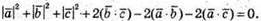
Тоді 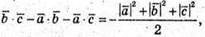
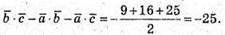
30.
Спростимо вираз
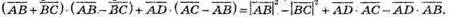
Оскільки ABCD правильний тетраедр 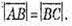
Отримуємо:
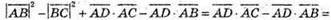
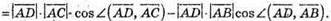
Оскільки ABCD – правильний тетраедр
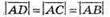
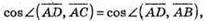 а отже
а отже