ПЕРПЕНДИКУЛЯРНІ І ПАРАЛЕЛЬНІ ПРЯМІ
РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ
& 5. ПЕРПЕНДИКУЛЯРНІ І ПАРАЛЕЛЬНІ ПРЯМІ
Пригадайте, як можуть розташовуватися на площині дві прямі. Якщо вони перетинаються, то утворюють чотири кути – дві пари вертикальних кутів. Йдеться про кути, менші від розгорнутого.
Менший із цих кутів вважають кутом між даними прямими. Наприклад, на малюнку 56 прямі АВ і CD перетинаються під кутом 50°.
Кажуть також, що кут між прямими АВ і CD дорівнює 50°. Якщо дві прямі, перетинаючись, утворюють чотири прямі кути, кажуть, що вони перетинаються
Дві прямі, які перетинаються під прямим кутом, називають перпендикулярними прямими.
Прямі а і b на малюнку 57 перпендикулярні одна до одної. Коротко пишуть: а ⏊ b, або b ⏊ а.
Відрізки або промені називають перпендикулярними, якщо вони лежать на перпендикулярних прямих.
Якщо відрізок АВ лежить на прямій, перпендикулярній до прямої а, кажуть, що відрізок АВ перпендикулярний до прямої а. Якщо при цьому точка В належить прямій а, то відрізок АВ називають перпендикуляром, проведеним з точки А на пряму а (мал. 58). Точку В називають основою перпендикуляра, а довжину перпендикуляра АВ –
Через довільну точку Р завжди можна провести пряму, перпендикулярну до даної прямої а.
Це можна зробити, користуючись косинцем (мал. 59) або транспортиром (мал. 60).
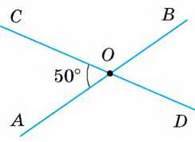
Мал. 56
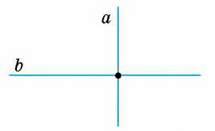
Мал. 57
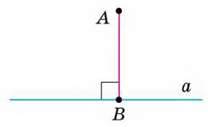
Мал. 58
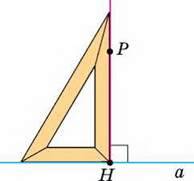
Мал. 59
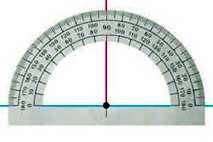
Мал. 60
Згодом дізнаєтесь, як можна виконати таку побудову за допомогою лінійки і циркуля. Можна довести, що існує тільки одна пряма, яка перпендикулярна до даної прямої і проходить через дану точку.
Не кожні дві прямі перетинаються. Особливої уваги заслуговують прямі, які не перетинаються і лежать в одній площині.
Дві прямі на площині називають паралельними, якщо вони не перетинаються. Якщо прямі а і b паралельні, пишуть: а ‖ b (мал. 61).
Уявлення про паралельні прямі дають лінії в зошиті, лінії нотного стану (мал. 62), протилежні ребра бруска.
Два відрізки або промені називають паралельними, якщо вони лежать на паралельних прямих. Наприклад, якщо ABCD – прямокутник, то АВ ‖ DC і ВС ‖ АD.
Через будь-яку точку Р, яка не лежить на прямій а, можна провести пряму, паралельну прямій а (мал. 63, а). Для цього можна через точку Р провести пряму с, перпендикулярну до прямої а, а потім пряму b, перпендикулярну до прямої с (мал. 63. б). За такої побудови завжди b ‖ а. Можна скористатися також лінійкою і косинцем.
Як проводити паралельні прямі, користуючись лінійкою і циркулем, дізнаєтесь пізніше.
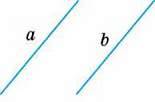
Мал. 61

Мал. 62
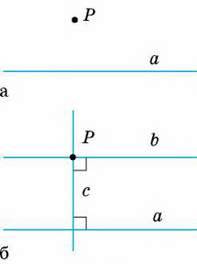
Мал. 63
Для допитливих
1. Можна довести (спробуйте!), що дві прямі однієї площини, які перпендикулярні до третьої прямої, – паралельні. Тобто, якщо а ⏊ с, b ⏊ с, то а ‖ b.
Але якщо прямі а і Ь не належать одній площині, то таке твердження неправильне. Наприклад, якщо ABCDA1B1C1D1 – куб, то АВ ⏊ ВВ1 і В1С1 ⏊ ВB1 але прямі АВ і B1C1 не паралельні (мал. 64).
2. Слово паралельні походить від грецького слова “параллелос”, яке означає: ті, що йдуть поруч. Якщо говорять, що якась пряма паралельна, то обов’язково слід сказати, якій саме прямій вона паралельна.
Отже, паралельність прямих – це своєрідне відношення між двома прямими. Відношення паралельності прямих має таку властивість: якщо a ‖ b то і b ‖ а.
Іншими відношеннями є перпендикулярність прямих, рівність кутів тощо. Знаки цих відношень: ‖, ⏊, =.
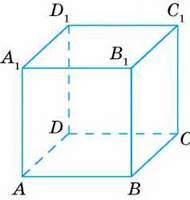
Мал. 64
Запитання і завдання для самоконтролю
1. Що таке кут між прямими?
2. Сформулюйте означення перпендикулярних прямих.
3. Які відрізки називають перпендикулярними?
4. Які дві прямі називають паралельними?
5. Які відрізки називають паралельними?
6. За допомогою яких креслярських інструментів можна провести пряму, перпендикулярну до даної прямої? Як це роблять?
7. Як можна провести пряму, паралельну даній прямій?
Виконаємо разом
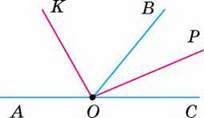
1. Доведіть, що бісектриси суміжних кутів перпендикулярні.
– Нехай ∠АОВ і ∠ВОС – суміжні кути. ОК і ОР – їх бісектриси (мал. 65). ∠KOP = ∠КОВ + ∠ВОР. Оскільки ОК і ОР – бісектриси, то
∠КОВ =  ∠AОВ, ∠ВОР =
∠AОВ, ∠ВОР =  ∠ВОС.
∠ВОС.
Тоді ∠КОР =  ∠АОВ +
∠АОВ +  ∠ВОС =
∠ВОС =  (∠АОВ + ∠ВОС) =
(∠АОВ + ∠ВОС) =  ∙ 180° = 90°. Отже, ОК ⏊ ОР.
∙ 180° = 90°. Отже, ОК ⏊ ОР.
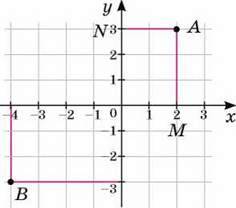
2. Позначте на координатній площині точки А (2; 3) і В (-4; -3). Знайдіть відстань від цих точок до осей координат, якщо довжина одиничного відрізка дорівнює 1 см.
З точок А і В опустимо перпендикуляри на осі координат (мал. 66). Довжина відрізка AM – відстань від точки А до осі ОХ, а довжина відрізка AN – відстань від точки А до осі OY. З малюнка видно, що AM = 3 см, a AN = 2 см.
Аналогічно встановлюємо, що відстань від точки В до осей координат дорівнює 3 см і 4 см.
Мал. 65
Мал. 66
ЗАДАЧІ І ВПРАВИ
Виконайте усно
131. Наведіть приклади матеріальних моделей:
А) перпендикулярних прямих;
Б) паралельних прямих.
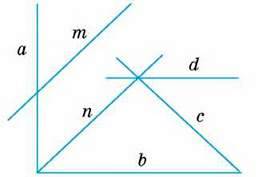
132. Які з прямих, зображених на малюнку 67:
А) перпендикулярні;
Б) паралельні?
Мал. 67
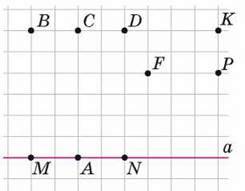
133. Користуючись клітинками зошита (мал. 68) укажіть:
1) через яку точку пройде пряма, яка:
А) перпендикулярна до прямої а і проходить через точку А;
Б) перпендикулярна до прямої а і проходить через точку D;
В) паралельна прямій а і проходить через точку F;
Г) паралельна прямій а і проходить через точку К;
2) яке з тверджень правильне:
А) АВ ⏊ а; б) ВМ ⏊ а;
В) КР ⏊а; г) FK ‖ а;
Г) ВС ‖ а; д) КР ‖ а.
Мал. 68
134. ABCDA1B1C1D1 – прямокутний паралелепіпед (мал. 69).
1) Назвіть відрізки:
А) паралельні відрізку АА1;
Б) паралельні відрізку AD;
В) перпендикулярні до відрізка АА1;
Г) перпендикулярні до відрізка AD.
2) Яке з тверджень правильне:
А) АА1 ⏊ AD; б) В1С1 ⏊ A1B1;
В) DC ⏊ AB; Г)D1B ⏊ DB;
Г) СD ‖ С1D1; д)A1D1 ‖ AD;
E) DD1 ‖ A1D1; e) CD ‖ AB?
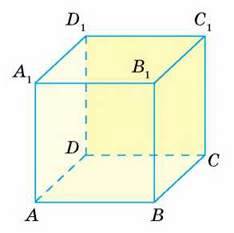
Мал. 69
А
135. Проведіть пряму а і позначте точки М і N такі, що М ∈ а, N ∉ а. Користуючись клітинками зошита, проведіть через точки М і N прямі, перпендикулярні до прямої а.
136. Точки М і N лежать по різні боки від прямої а. Користуючись клітинками зошита, через точки М і N проведіть прямі, паралельні прямій а.
137. Точка А не лежить на прямій с. Скільки прямих, перпендикулярних до прямої с, можна провести через точку А? Чому?
138. Точка К не лежить на прямій а. Користуючись косинцем, побудуйте перпендикуляр, проведений із точки К до прямої а.
139. Назвіть десять пар перпендикулярних відрізків, що є на малюнку 70. Чи є перпендикулярами до прямої КР відрізки АН, BH, СН, АВ, ВС?
140. Відомо, що а ‖ b. Чи правильно, що b ‖ а?
141. Промені АВ і CD не перетинаються. Чи можна стверджувати, що вони паралельні?
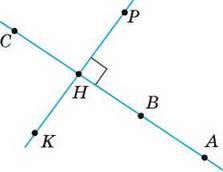
Мал. 70
142. Використовуючи малюнок 67 і символи ⏊ і ‖, заповніть пропуски: а) а… b; б) m… n; в) n… с; г) а… d; г) m… с; д) b… d.
143. Перпендикулярні прямі АВ та CD перетинаються в точці О. ОМ – бісектриса кута СОВ. Знайдіть ∠АОМ і ∠MOD.
144. Позначте на координатній площині точки А (-3; 4), В (1; 8), С (4; 5), D (-2; -1). Перевірте, чи перпендикулярні прямі АD і DC, АВ і ВС. Чи паралельні прямі АВ і CD, AD і BС?
145. Позначте на координатній площині точки А (-3; -1) і B (2; 4). Через ці точки проведіть прямі, перпендикулярні до прямої АВ. Знайдіть координати точок перетину побудованих прямих з осями координат. Чи паралельні побудовані прямі?
146. За допомогою транспортира побудуйте ∠АОВ = 30°. Позначте точку М таку, що М ∈ ОА і ОМ = 4 см. Із точки М опустіть перпендикуляр на пряму ОB. Виміряйте відстань від точки М до ОB.
147. За допомогою транспортира побудуйте ∠АОВ = 130°. Позначте М ∈ ОА. Із точки М опустіть перпендикуляр на пряму ОВ. Чи лежатиме основа перпендикуляра на промені ОВ? А на прямій ОВ?
148. ∠AОВ = 90°, М – внутрішня точка кута АОB. Через точку М проведіть прямі, паралельні сторонам кута. Переконайтеся, що побудовані прямі перпендикулярні.
149. ∠AОВ = 90°, М – довільна точка бісектриси кута АОВ. Виміряйте відстані від точки М до променів ОВ і ОА. Порівняйте ці відстані.
Б
150. ∠AОВ і ∠ВОС – суміжні кути. ОМ – внутрішній промінь кута АОВ, ОМ ⏊ АС. Чому дорівнює ∠МОВ, якщо:
А) ∠ВОС = 40°; б) ∠AОВ – ∠ВОС = 30°;
В) ∠АОВ : ∠ВОС = 3 : 2; г) ∠ВОС =  ∠АОВ?
∠АОВ?
151. Три прямі АВ, CD, MN перетинаються в точці О (мал. 71). Доведіть, що CD ⏊ MN, якщо:
А) ∠AОМ = 130°, ∠СОВ = 140°;
Б) ∠СОМ = ∠АОС + ∠МОВ;
В) ∠АОМ = 135°, ОВ – бісектриса кута MOD.
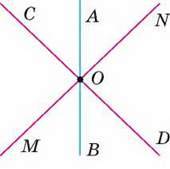
Мал. 71
152. ∠AОВ = 90°. Побудуйте точку М, яка лежить у внутрішній області кута АОВ на відстані 2 см від кожної сторони кута.
153. Побудуйте перпендикулярні прямі а, с і точку М, яка лежить на відстані 3 см від прямої а і на відстані 1 см від прямої с.
154. За допомогою транспортира побудуйте ∠АОВ = 80° і проведіть його бісектрису ОМ. Через довільну точку К цієї бісектриси проведіть прямі, перпендикулярні до сторін кута. Виміряйте відстані від точки К до сторін кута і порівняйте їх.
155. Розв’яжіть попередню задачу, якщо ∠АОВ дорівнює 60°, 90° і 130°. Сформулюйте припущення про відстань від точок бісектриси кута до сторін цього кута.
156. За допомогою транспортира побудуйте ∠АОВ = 60° і проведіть його бісектрису ОМ. Через довільну точ
Ку К цієї бісектриси проведіть пряму EF, перпендикулярну до ОМ. Порівняйте довжини відрізків ОЕ і OF, якщо Е ∈ ОА, F ∈ ОВ.
157. Розв’яжіть попередню задачу, якщо ∠AОВ дорівнює 80°, 90° і 120°. Сформулюйте припущення про властивість прямої, перпендикулярної до бісектриси кута.
158. Прикладаючи косинець то одним, то іншим боком, учень через точку А провів два перпендикуляри до прямої а (мал. 72). Що можна сказати про такий косинець?
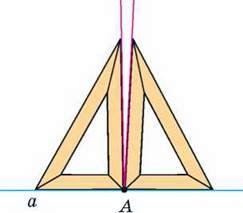
Мал. 72
Практичне завдання
159. Підготуйте презентацію на тему:
А) “Паралельні прямі навколо нас”; б) “Перпендикулярні прямі навколо нас”.
ЗАДАЧI ДЛЯ ПОВТОРЕННЯ
160. Позначте на прямій а точки А, В, С, D, М так, щоб точка В лежала між точками А і D, точка М – між А і В, а точка С – між В і D.
161. Чи належить точка К відрізку АВ, якщо АК = 3 см, ВК = 5 см, АВ = 7 см?
162. Знайдіть міри суміжних кутів, якщо вони пропорційні числам:
А) 1 і 2; 6)1 і 4; в) 4 і 5; г)  і
і  .
.
163. Периметр чотирикутника дорівнює Р. Знайдіть довжини його сторін, якщо вони пропорційні числам:
А) 1, 2; З і 4; б) 3, 5, З і 7; в)  ,
,  ,
,  i 1.
i 1.