Поняття про обернену функцію
Математика – Алгебра
Тригонометричні функції
Поняття про обернену функцію
Функція, яка приймає кожне своє значення в єдиній точці області визначення, є Оборотною.
У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає.
Інакше кажучи, якщо функція 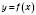 є оборотною й число а належить до її області значень
є оборотною й число а належить до її області значень 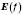 , то рівняння
, то рівняння 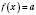 має розв’язок, причому єдиний.
має розв’язок, причому єдиний.
Оберненою до даної оборотної
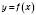 називається така функція
називається така функція 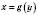 , яка кожному із множини значень функції
, яка кожному із множини значень функції 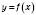 ставить у відповідність єдине число x з області визначення.
ставить у відповідність єдине число x з області визначення.Якщо аргумент і функцію в записі
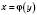 позначити звичайним способом, отримаємо
позначити звичайним способом, отримаємо 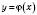 .
.Графік функції g, оберненої до функції f, симетричний графіку f відносно прямої
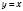 .
.Якщо функція f зростає (або спадає) на проміжку I, то вона є оборотною. Обернена до f функція g, яка визначена в області значень f, теж є зростаючою (або спадною).
1. На проміжку
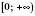 функція
функція 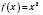 є оборотною. Оберненою до неї на цьому проміжку є функція
є оборотною. Оберненою до неї на цьому проміжку є функція 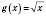 .
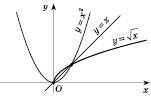
.На рисунку зображені функція
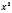 і обернена до неї функція
і обернена до неї функція 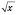 :
:
2. y = arcsin x – функція, обернена до
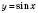 , якщо
, якщо 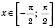 .
.Отже, запис
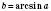 Означає, що
Означає, що 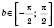 ;
; 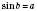 .
.Зверніть увагу: у деяких випадках не можна назвати точного значення
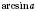 . Наприклад,
. Наприклад, 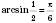 , але для
, але для 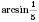 можемо знайти тільки наближене значення.
можемо знайти тільки наближене значення.Властивості функції
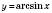 :
:1) область визначення
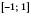 ;
;2) область значень
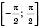 ;
;3) функція непарна, бо
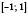 – симетрична відносно 0;
– симетрична відносно 0; 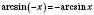 .
.Отже, графік
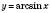 Симетричний відносно початку координат;
Симетричний відносно початку координат;4) функція не є періодичною;
5)
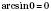 ;
;6) функція зростаюча;
7)
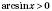 при
при 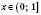 ,
,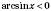 при
при 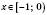 ;
;8) найбільше значення –
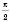 , якщо
, якщо 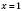 , найменше –
, найменше – 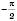 , якщо
, якщо 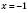 .
.Графік функції
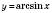 зображений на рисунку:
зображений на рисунку: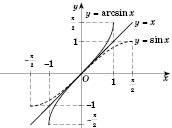
Зверніть увагу на рівності:
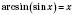 ;
;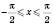 ;
;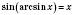 ;
; 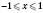 .
.Зверніть увагу:
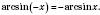
3. y = arccos x – функція, обернена до
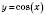 , якщо
, якщо 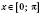 .
.Отже, запис
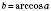 означає, що
означає, що 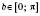 ;
; 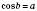 .
.Властивості функції y = arccosx:
1)
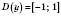 ;
;2)
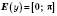 ;
;3) функція не є ні парною, ні непарною;
4) функція не є періодичною;
5)
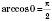 ,
, 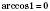 ;
;6) функція спадна;
7) функція додатна на всій області визначення;
8) найбільше значення –
 , якщо
, якщо 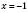 , найменше – 0, якщо
, найменше – 0, якщо 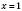 .
.Графік функції
 зображений на рисунку:
зображений на рисунку: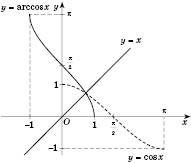
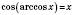 ;
; 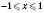 ;
;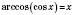 ;
; 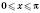 .
.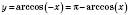 .
.4.
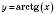 – функція, обернена до
– функція, обернена до 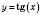 , якщо
, якщо 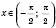 .
.Запис b = arctg(a) означає:
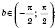
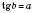 .
.Властивості функції y = arctgx:
1)
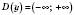 ;
;2)
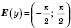 ;
;3) функція непарна.
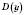 симетрична відносно 0,
симетрична відносно 0, 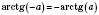 .
.Графік симетричний відносно початку координат;
4) функція не є періодичною;
5)
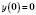 ;
;6) функція зростаюча;
7)
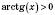 , якщо
, якщо 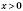 ,
,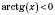 , якщо
, якщо 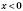 ;
;8) функція не набуває найбільшого і найменшого значень.
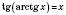 , якщо
, якщо 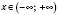 ;
;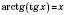 , якщо
, якщо 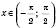 ;
;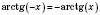 .
.Графік функції
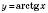 зображений на рисунку:
зображений на рисунку: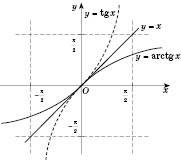
5.
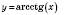 – функція, обернена до
– функція, обернена до 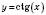 , якщо
, якщо 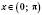 .
.Запис
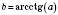 означає, що
означає, що 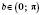 ;
; 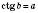 .
.Властивості функції y = arcctgx:
1)
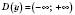 ;
;2)
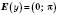 ;
;3) функція не є ні парною, ні непарною;
4) функція не є періодичною;
5)
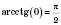 ,
,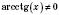 при жодному значенні х;
при жодному значенні х;6) функція спадна;
7) додатна на всій області визначень;
8) функція не набуває найбільшого і найменшого значень.
Графік функції
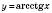 зображений на рисунку:
зображений на рисунку: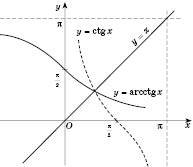
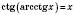 ,
, 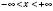 ,
,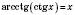 ,
, 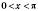 ,
,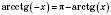 ,
, 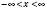 .
.