Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = a
УРОК 21
Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = а
Мета уроку: засвоєння учнями виведення і застосування формули для коренів рівняння sin t = а.
Обладнання: Таблиця “Рівняння sin t = а”.
І. Перевірка домашнього завдання
1. Відповіді на питання, що виникли при виконанні домашніх завдань.
2. Самостійна робота.
Варіант 1
Розв’яжіть рівняння:
А) 2cos 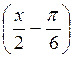 =
=  . (3 бали)
. (3 бали)
Б) 2cos2x + cos x – 1 = 0. (3 бали)
В) 4cos x = 4 – sin x. (3 бали)
Г) sin 3х sin x – cos
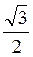 . (3 бали)
. (3 бали)Варіант 2
Розв’яжіть рівняння :
А) 2 cos 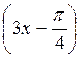 =
=  . (3 бали)
. (3 бали)
Б) 2cos2x – cosx – 1 = 0. (3 бали)
В) 8 sin2х + cosx + 1 = 0. (3 бали)
Г) sin2 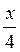 – cos2
– cos2 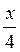 = 1. (3 бали)
= 1. (3 бали)
Відповідь:
B-1. a) ±
± +4?n, n
+4?n, n Z; б) ±
Z; б) ± +2?n і?+2?n, n
+2?n і?+2?n, n Z; в)2?n, n
Z; в)2?n, n Z; г) ±
Z; г) ±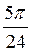 +?n, n
+?n, n Z.
Z.
В-2. a) 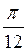 ±
±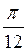 +
+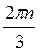 , n
, n Z;
Z;
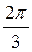 +2?n, n
+2?n, n Z; в) n+2?n, n
Z; в) n+2?n, n Z; г) 4?n, n
Z; г) 4?n, n Z.
Z.II. Повідомлення теми уроку
III. Сприймання і усвідомлення матеріалу про розв’язування рівняння sin t = a
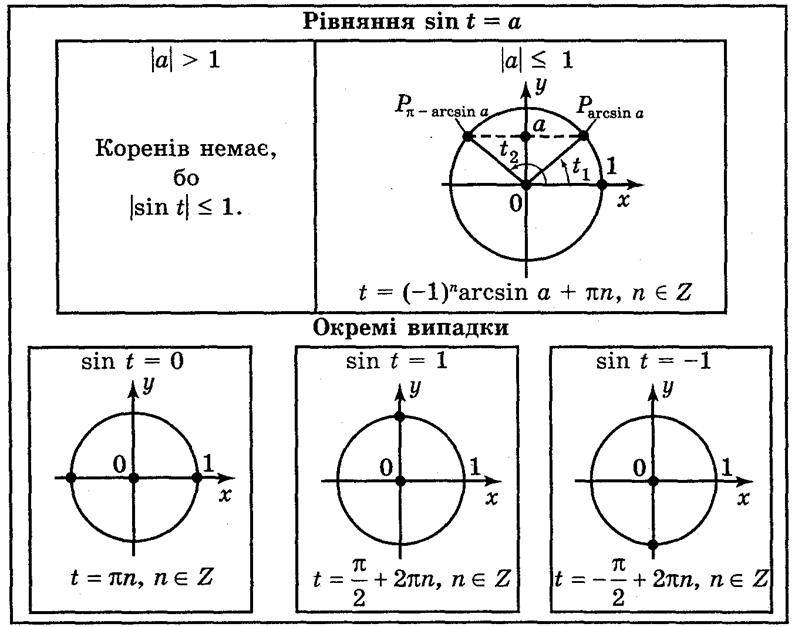
Демонструється таблиця 9.
Пояснення вчителя
1) Якщо |а| > 1, то рівняння не має розв’язків, поскільки |sin x| 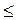 1 для будь-якого t.
1 для будь-якого t.
2) Якщо |а| < 1, то, враховуючи те, що sin t – ордината точки Рt одиничного кола, маємо: ординату, рівну а, мають дві точки одиничного кола (на осі OY відкладаємо число а і через цю точку проведемо пряму, перпендикулярну до осі ординат (рис. 123), яка перетне коло у двох токах – 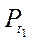 і
і 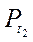 ):
):
T1 = arcsin a + 2?n, n Z,
Z,
T2 = n – arcsin а + 2?n, n Z.
Z.
Ці дві формули можна записати у вигляді однієї формули:
T = (-1)k arcsin a + nk, k Z (1)
Z (1)
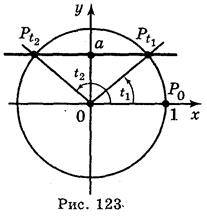
Неважко впевнитися, що при парному k = 2? маємо:
T1 = (-1)2n arcsin а + 2?n або t1 = arcsin a + 2?n, n Z;
Z;
При непарному k = 2n + 1 маємо:
T2 = (-1)2n+1 arcsin а + (2n + 1)n;
T2 = – arcsin а + 2?n + n;
T2 = n – arcsin a + 2?n, n Z.
Z.
3) Якщо а = 1, то, враховуючи те, що sint – це ордината точки Pt (одиничного кола, маємо: ординату, рівну 1, має точка Рt утворена із точки Р0(1;0) поворотом на кут  + 2?n, n
+ 2?n, n Z.
Z.
Отже, t =  + 2?n, n
+ 2?n, n Z. Якщо а = -1, то t = –
Z. Якщо а = -1, то t = – + 2?n, n
+ 2?n, n Z.
Z.
4) Якщо а = 0, маємо t = 0 + ?n; t = ?n, n Z.
Z.
Розглянемо приклади.
Приклад 1. Розв’яжіть рівняння sinx = 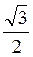 .
.
Згідно з формулою (1) маємо: х = (-1)n arcsin 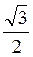 + ?n, n
+ ?n, n Z.
Z.
Оскільки arcsin 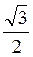 =
=  , то х = (-1)n
, то х = (-1)n  + ?n, n
+ ?n, n Z.
Z.
Відповідь: (-1)n  + ?n, n
+ ?n, n Z.
Z.
Приклад 2. Розв’яжіть рівняння sin х = –  .
.
Згідно з формулою (1) маємо: х = (-1)n arcsin 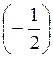 + ?n, n
+ ?n, n Z.
Z.
Оскільки arcsin 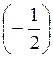 = –
= –  , то х =(-1)n –
, то х =(-1)n –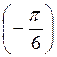 + ?n, n
+ ?n, n Z; х = (-1)n+1 + ?n, n
Z; х = (-1)n+1 + ?n, n Z.
Z.
Відповідь: (-1)n+1 + ?n, n Z.
Z.
Приклад 3. Розв’яжіть рівняння sin x = 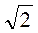 – 1.
– 1.
Згідно з формулою (1) маємо: х = (-1)n arcsin(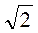 – 1) + ?n, n
– 1) + ?n, n Z.
Z.
Значення arcsin( -1) знайдемо за допомогою мікрокалькулятора:
-1) знайдемо за допомогою мікрокалькулятора:
Arcsin(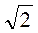 – 1)
– 1) 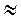 0,427, тоді х
0,427, тоді х 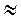 (-1)n – 0,427 + ?n, n
(-1)n – 0,427 + ?n, n Z.
Z.
Відповідь: (-1)n – arcsin( -1) + ?n
-1) + ?n 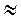 (-1)n – 0,427 + ?n, n
(-1)n – 0,427 + ?n, n Z.
Z.
IV. Осмислення вивченого матеріалу
Розв’яжіть рівняння.
1. a) 2sin х – 1 = 0; б) 2sin 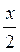 = – 1; в) 2sin
= – 1; в) 2sin 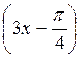 = –
= –  ; г) 2sin
; г) 2sin 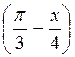 =
=  .
.
Відповідь: а) (-1)n + ?n, n
+ ?n, n Z; б) (-1)n+1
Z; б) (-1)n+1 + 2?n, n
+ 2?n, n Z; в)
Z; в) 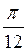 +(-1) n+1
+(-1) n+1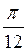 +
+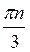 , n
, n Z; г)
Z; г) 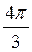 +(-1)n+1
+(-1)n+1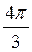 + 4?n, n
+ 4?n, n Z.
Z.
2. a) sin 3х cos х – cos 3х sin х = 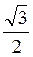 ;
;
Б) sin 2x cos 2x = – 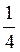 ;
;
В) sin 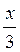 Cos
Cos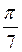 – cos
– cos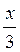 Sin
Sin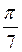 =
= 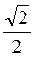 ;
;
Г) cos 2x sin 3х + sin 2x cos 3x = 1.
Відповідь: а) (-1)n +
+ 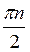 , n
, n Z; б) (-1)n+1
Z; б) (-1)n+1 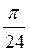 +
+ 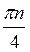 , n
, n Z; в)
Z; в) 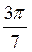 (-1)n
(-1)n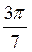 +3 ?n, n
+3 ?n, n Z; г)
Z; г) 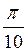 +
+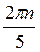 , n
, n Z.
Z.
3. а) (2sin х – 1)(3sin х + 1) = 0; б) (4sin 3х – 1)(2sin х + 3) = 0.
Відповідь: а) (-1)n + ?n і (-1)n+1arcsin
+ ?n і (-1)n+1arcsin 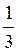 + ?n, n
+ ?n, n Z; б) (-1)n
Z; б) (-1)n 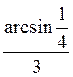 +
+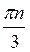 , n
, n Z.
Z.
V. Підведення підсумків уроку
VI. Домашнє завдання
Розділ II § 2 (1). Запитання і завдання для повторення до розділу II № 13-15. Вправи № 1 (6; 7; 8; 14; 17; 18), № 2 (3).