Головна ⇒ 📌Довідник з математики ⇒ Розв’язування нерівностей з однією змінною
Розв’язування нерівностей з однією змінною
Математика – Алгебра
Нерівності
Розв’язування нерівностей з однією змінною
Розв’язком нерівності з однією змінною називається значення цієї змінної, яке перетворює її на правильну числову нерівність.
Розв’язати нерівність означає знайти всі її розв’язки або довести, що їх немає.
Дві нерівності називають Рівносильними, якщо вони мають одні й ті самі розв’язки або не мають розв’язків.
Числові проміжки
Множину всіх дійсних чисел, менших від 10, називають проміжком від мінус нескінченності до 10 і
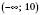. На координатній прямій ці числа розташовані ліворуч від числа 10, що можна наочно зобразити так, як це зроблено на рисунку зліва або на рисунку справа:
Зверніть увагу: коли на координатній прямій зображують числові проміжки, 0 та одиничний відрізок не позначають.
Множину всіх чисел, не більших від 10, записують у вигляді
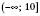і зображують так, як це зроблено на рисунку зліва або на рисунку справа:
Інші випадки зображення числових проміжків на координатній прямій наведені на
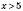
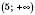
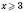
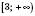
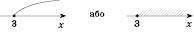
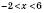
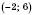
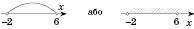
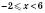
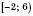
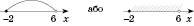
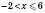
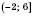
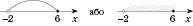
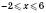
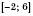
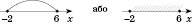
x – довільне число
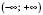
Властивості нерівностей зі змінними
1. Якщо з однієї частини нерівності перенести в іншу доданок із протилежним знаком, то дістанемо нерівність, рівносильну даній.
2. Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то дістанемо нерівність, рівносильну даній.
3. Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число, змінивши при цьому знак нерівності на протилежний, то дістанемо нерівність, рівносильну даній.
Множини розв’язків нерівностей можна записувати у вигляді проміжків.
Приклади
1) 
, 
, 
, 
, 
.
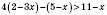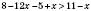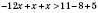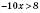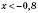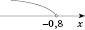
Відповідь: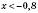 
(можна записати у вигляді 
.
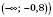2) 
,
,
, 
,
.
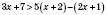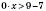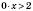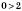Відповідь: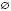 
(розв’язків немає).
3) 
,
, 
.
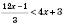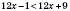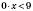Відповідь: x – довільне число (або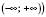 
.
4) Приклади нерівностей, котрі мають один чи кілька ізольованих розв’язків:
а)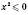 
, б)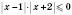 
,
; 
, 
.
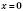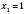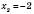5) При яких значеннях х має зміст вираз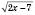 
?
Цей вираз має зміст при тих і тільки тих значеннях х, які є розв’язками нерівності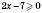 
, 
.
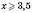Відповідь: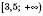 
.
(1 votes, average: 5.00 out of 5)
Loading...Related posts:
- Системи нерівностей з однією змінною Математика – Алгебра Нерівності Системи нерівностей з однією змінною Розв’язком системи нерівностей з однією змінною називають значення змінної, яке є розв’язком кожної нерівності даної системи. Розв’язати систему нерівностей означає знайти всі її розв’язки або показати, що їх немає. Щоб розв’язати систему нерівностей, кожну її нерівність поступово спрощують, замінюючи рівносильною. Розглянемо на простих прикладах, як застосувати […]...
- Нерівність з однією змінною. Система та сукупність нерівностей з однією змінною УРОК № 9 Тема. Нерівність з однією змінною. Система та сукупність нерівностей з однією змінною Мета уроку: засвоєння учнями змісту понять: нерівність з однією змінною, розв’язок нерівності з однією змінною та що означає розв’язати нерівність з однією змінною; система нерівностей з однією змінною, розв’язок системи нерівностей з однією змінною та що означає розв’язати систему нерівностей […]...
- Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною УРОК № 14 Тема. Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною Мета уроку: закріплення учнями знань змісту понять: нерівність з однією змінною, розв’язок нерівності з однією змінною та що означає розв’язати нерівність з однією змінною; система нерівностей з однією змінною, розв’язок системи нерівностей з однією змінною та що означає розв’язати систему нерівностей з […]...
- Нерівності з однією змінною УРОК № 63 Тема. Нерівності з однією змінною Тестові завдання 1. Дано нерівності: 1) -2х2 + х + 6 < 0; 2) 2х2 + х + 7 ? 0; 3) х2 > 0; 4) -3х2 – х – 6 < 0. 2. Яка з даних нерівностей виконується при будь-яких значеннях x? а) усі; б) 2; […]...
- Числові та лінійні нерівності УРОК № 60 Тема. Числові та лінійні нерівності Тестові завдання 1. Яку подвійну нерівність задовольняє множина чисел, поданих на рисунку? А) -4 < x < 8; Б) -4 < х < 8; В) -4 < х < 8; Г) -4 < х < 8. 2. Відомо, що х < у. Яка з наведених нерівностей є […]...
- Властивості числових нерівностей Математика – Алгебра Нерівності Властивості числових нерівностей a, b, с, d – довільні числа. 1. Якщо і , то . 2. Якщо до обох частин правильної нерівності додати одне й те саме число, то дістанемо правильну нерівність. 3. Якщо обидві частини правильної нерівності помножити на одне й те саме додатне число, то дістанемо правильну нерівність. […]...
- Лінійні нерівності з однією змінною УРОК № 12 Тема. Лінійні нерівності з однією змінною Мета уроку: домогтися закріплення учнями змісту: означення рівносильних нерівностей та властивостей рівносильних нерівностей; означення лінійної нерівності з однією змінною та схеми Ті розв’язування залежно від різних значень коефіцієнтів. Доповнити знання учнів уявленням про схему дій при розв’язування нерівностей з однією змінною, що містять дроби із числовими […]...
- Розв’язування нерівностей, що містять показникову функцію УРОК 49 Тема. Розв’язування нерівностей, що містять показникову функцію Мета уроку. Познайомити учнів зі способами розв’язування показникових нерівностей. І. Перевірка домашнього завдання Відповіді на запитання, що виникли в учнів під час виконання домашніх завдань. II. Аналіз самостійної роботи, проведеної на попередньому уроці ІІІ. Сприймання і усвідомлення розв’язування найпростіших показникових нерівностей та тих, що безпосередньо зводяться […]...
- Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 23. Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них Ми знаємо, як розв’язувати рівняння 2х = -8; х – 5; 0,01х -17. Кожне із цих рівнянь має вигляд ах = b, де х – змінна, а і b […]...
- Лінійні рівняння з однією змінною 793. Лінійними рівняннями є рівняння: а) 2/9х = 8; в) -2,7y = 0. 794. а) 56х = 64; рівняння має 1 корінь, Б) 0х = -2; рівняння не має коренів; В) 8х = 0; рівняння має 1 корінь, х = 0; Г) 0у = 0; рівняння має безліч коренів. 795. а) 6х = 42; х […]...
- Розв’язування показникових нерівностей УРОК 50 Тема. Розв’язування показникових нерівностей Мета уроку. Формування умінь учнів розв’язувати показникові нерівності. І. Перевірка домашнього завдання 1. Відповіді на запитання, що виникли в учнів при виконанні домашніх завдань. 2. Усне розв’язування показникових нерівностей з використанням таблиці 21 для усних обчислень “Показникові нерівності “. 1 2 3 4 5 1 2х > 8 2х […]...
- Розв’язування тригонометричних нерівностей УРОК 30 Тема. Розв’язування тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати тригонометричні нерівності. І. Перевірка домашнього завдання. 1. Відповіді на запитання, які виникли у учнів при виконанні домашнього завдання. 2. Фронтальна бесіда з учнями з використанням рис. 135. 1) Які дуги відповідають нерівностям: Tg t > a, tg t < a, tg t > […]...
- Розв’язування найпростіших тригонометричних нерівностей УРОК 29 Тема. Розв’язування найпростіших тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати найпростіші тригонометричні нерівності: tg t > a, tgt < a, ctg t < a, ctg t > a (tgt a, tgt a, ctg t a, ctg t a). І. Перевірка домашнього завдання 1. Відповіді на запитання, які виникли в учнів у процесі […]...
- Лінійні нерівності та їхні системи УРОК № 61 Тема. Лінійні нерівності та їхні системи Тестове завдання 1. Знайдіть переріз проміжків (-6; 7] і (-4; 25]. А) [7; 25); б) [-4; 7); в) (-6; 25]; г) (-4; 7]. 2. Розв’яжіть нерівність . A) k < 1,125; б) k? ; в) k? 1,125; г) немає розв’язків. 3. При яких х має зміст […]...
- Розв’язування логарифмічних нерівностей УРОК 61 Тема. Розв’язування логарифмічних нерівностей Мета уроку. Формування умінь учнів розв’язувати логарифмічні нерівності І. Перевірка домашнього завдання Перевірити наявність виконаних домашніх завдань та відповісти на запитання, що виникли в учнів при виконанні цих завдань. II. Сприймання і усвідомлення розв’язування логарифмічних нерівностей (які розв’язуються введенням нової змінної) Приклад 1. Розв’яжіть нерівність log х – log5 […]...
- Рівняння. Нерівності зі змінною Рівняння. Нерівності зі змінною 1 Розбий записи на дві групи. Назви кожну групу. 27 + х = 51 27 + х < 51 40 ∙ р > 160 2 Згадай, що ти знаєш про рівняння; про нерівності зі змінною. Розглянь, як учні розв’язали рівняння та нерівність способом добору. Прокоментуй їхні дії. Із чисел 1, 2, […]...
- Розв’язування ірраціональних нерівностей УРОК 39 Тема. Розв’язування ірраціональних нерівностей Мета уроку. Познайомити учнів з узагальненим методом інтервалів. Формування умінь розв’язувати ірраціональні нерівності. І. Перевірка домашнього завдання 1. Перевірити розв’язування вправ № 71 (3), 67 (1), 79 (1) за розв’язаннями на дошці, заготовленими до уроку. 2. Самостійна робота Розв’яжіть рівняння: А) = . (4 бали) Б) – = 2. […]...
- Нерівності Математика – Алгебра Нерівності Число а вважається більшим від b, якщо різниця – число додатне. Число a менше від b, якщо різниця – число від’ємне. Якщо , то числа a і b рівні. На координатній прямій меншому числу відповідає точка, що лежить ліворуч від точки, яка відповідає більшому числу. Позначення: – a менше від b; […]...
- Лінійне рівняння з однією змінною Урок № 11 Тема. Лінійне рівняння з однією змінною Мета: перевірити рівень засвоєння знань, умінь та навичок, передбачених програмою, в ході вивчення названої теми. Тип уроку: контроль знань. Хід уроку І. Умова тематичної контрольної роботи Варіант 1 Варіант 2 № 1. Чи рівносильні рівняння? Чому? 3х + 4 = 7 та 2(х + 3) – […]...
- Розв’язування показникових рівнянь, систем і нерівностей УРОК 51 Тема. Розв’язування показникових рівнянь, систем і нерівностей Мета уроку. Формування умінь розв’язувати показникові рівняння, системи і нерівності. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування вправи № 2 (11; 13; 16). 2. Колективне розв’язування нерівностей, аналогічних домашнім: вправи № 2 (30; 31). II. Аналіз самостійної роботи, проведеної на попередньому уроці III. Формування […]...
- Розв’язування лінійних рівнянь з однією змінною Урок № 99 Тема. Розв’язування лінійних рівнянь з однією змінною Мета: закріпити знання учнів про властивості рівносильності рівнянь та способи їх застосування для розв’язування лінійних рівнянь з однією змінною; вдосконалити вміння учнів розв’язувати лінійні рівняння з однією змінною з використанням зазначених вище знань. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент II. […]...
- ЛІНІЙНЕ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &20. ЛІНІЙНЕ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ Ви вже знаєте, що рівняння можна поділити на види за кількістю змінних. У цьому параграфі розглядатимемо рівняння з однією змінною. Запам’ятайте! Рівняння виду ах + b = 0, де х – змінна, а і b – деякі числа, називається лінійним рівнянням з […]...
- Основні властивості числових нерівностей УРОК № 4 Тема. Основні властивості числових нерівностей Мета уроку: домогтися засвоєння учнями змісту поняття “оцінити значення виразу”; закріпити знання учнів про зміст властивостей числових нерівностей та їхніх наслідків. Продовжити роботу з вироблення вмінь: відтворювати зміст вивчених властивостей, наслідків із них і їх доведення; застосовувати властивості числових нерівностей та наслідки з них для розв’язування вправ […]...
- Розв’язування тригонометричних рівнянь, систем та нерівностей УРОК 31 Тема. Розв’язування тригонометричних рівнянь, систем та нерівностей Мета уроку. Систематизувати навички і уміння розв’язувати тригонометричні рівняння, нерівності, системи. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування нерівностей із домашнього завдання. 2. Колективне розв’язування нерівностей: A) sin 2x sin x – cos 2x cos х . Sin 2x sin x – cos 2x […]...
- Рівняння. Нерівності зі змінною Мета: узагальнити й систематизувати навчальний досвід учнів відносно рівнянь і нерівностей зі змінною, способів їх розв’язування. Дидактичні задачі. Вдосконалювати навички позатабличного множення та ділення – усна лічба. Класифікувати записи на рівності та нерівності зі змінною. Актуалізувати поняття рівняння, “розв’язок рівняння”, “розв’язати рівняння”; поняття нерівності зі змінною; розуміння способу добору числа для розв’язування рівнянь та нерівностей. […]...
- Розв’язування найпростіших тригонометричних нерівностей Математика – Алгебра Тригонометричні функції Розв’язування найпростіших тригонометричних нерівностей Найзручнішим є спосіб розв’язування тригонометричних нерівностей за допомогою тригонометричного кола. Приклади 1) . Побудуємо одиничне коло (див. рисунок нижче). Проведемо пряму . Вона перетинає коло у двох точках. Одна з них відповідає куту або , друга – куту або . Ці дві точки розбивають коло на […]...
- Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання значення виразу УРОК № 6 Тема. Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання значення виразу Мета уроку: закріплення учнями змісту: властивостей числових нерівностей і теорем про почленне додавання та множення нерівностей; наслідків із властивостей числових нерівностей. Відпрацювання навичок: відтворювати зміст вивчених понять; застосовувати їх для розв’язування вправ: на порівняння виразів, на доведення нерівностей, […]...
- Числові нерівності. Доведення числових нерівностей УРОК № 2 Тема. Числові нерівності. Доведення числових нерівностей Мета уроку: домогтися засвоєння учнями змісту: додаткових нерівностей для суми взаємно обернених додатних чисел та середнього арифметичного двох невід’ємних чисел (у порівнянні з їх середнім геометричним) та доведення цих нерівностей; способу застосування доведених нерівностей при доведенні інших числових нерівностей. Продовжити роботу з вироблення вмінь: відтворювати зміст […]...
- Квадратна нерівність. Розв’язування квадратних нерівностей УРОК № 25 Тема. Квадратна нерівність. Розв’язування квадратних нерівностей Мета уроку: закріпити знання учнів про зміст означення квадратних нерівностей та схему їх розв’язування; удосконалити вміння учнів розв’язувати квадратні нерівності та нерівності, що зводяться до квадратних шляхом рівносильних перетворень, а також виробити вміння використовувати ці вміння під час розв’язування систем квадратних нерівностей та для розв’язування задач […]...
- Логарифмічні нерівності Математика – Алгебра Логарифмічна функція Логарифмічні нерівності Розв’язуючи логарифмічні нерівності, спираються на такі твердження. 1. Якщо , то нерівність рівносильна подвійній нерівності . Це твердження можна записати у вигляді: або 2. Якщо , то нерівність рівносильна подвійній нерівності . Це твердження можна записати у вигляді: або Зверніть увагу: при розв’язуванні логарифмічної нерівності немає сенсу окремо […]...
- Застосування модуля числа. Відстань між точками на координатній прямій Урок № 6 7 Тема. Застосування модуля числа. Відстань між точками на координатній прямій Мета: поглибити знання учнів про властивості модуля раціонального числа та відпрацювати навички застосування означення та властивостей модуля для розв’язування рівнянь та нерівностей. Тип уроку: застосування знань, умінь і навичок Хід уроку I. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. […]...
- Зображення нерівностей земної поверхні на плані та карті Географія Загальна географія Земля на плані та карті Зображення нерівностей земної поверхні на плані та карті Усі нерівності земної поверхні називають Рельєфом. Щоб зобразити його на плані чи карті, необхідно виміряти висоту окремих ділянок земної поверхні. Для цього використовують нівелір. За його допомогою визначають, на скільки метрів вершина горба вища за його підошву. Цей процес […]...
- Знаходження значень виразів на сумісні дії з багатоцифровими числами. Розширені задачі на зведення до одиниці. Складання і розв’язування нерівностей (№№ 1067-1075) Тема. Знаходження значень виразів на сумісні дії з багатоцифровими числами. Розширені задачі на зведення до одиниці. Складання і розв’язування нерівностей (№№ 1067 – 1075). Мета. Виправляти учнів у знаходженні значень виразів на сумісні дії з багатоцифровими числами; удосконалювати вміння розв’язувати задачі на зведення до одиниці; вчити складати і розв’язувати нерівності. Обладнання. Завдання для опитування учнів; […]...
- Порівняння раціональних чисел Урок № 69 Тема. Порівняння раціональних чисел Мета: відпрацювати навички порівняння раціональних чисел у комплексі із набутими раніше навичками (з теми про додатні і від’ємні числа). Тип уроку: застосування знань, умінь і навичок. Хід уроку І. Перевірка домашнього завдання. Актуалізація опорних знань А. Усні вправи (фронтальна робота із сигнальними картками або математичний диктант) 1. Закінчіть […]...
- Ознака паралельності прямої і площини Геометрія Стереометрія Ознака паралельності прямої і площини Теорема 1. Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині. Теорема 2. Якщо пряма паралельна площині, то на цій площині знайдеться пряма, яка паралельна даній прямій. Зверніть увагу: паралельність прямої і площини не означає, що ця пряма паралельна […]...
- Задачі на пропорційне ділення. Розв’язування рівнянь і нерівностей (№№ 849-857) Тема. Задачі на пропорційне ділення. Розв’язування рівнянь і нерівностей (№№ 849-857). Мета. Закріплювати вміння учнів розв’язувати задачі на пропорційне ділення; вчити складати задачі на пропорційне ділення за коротким записом; удосконалювати вміння розв’язувати рівняння і нерівності. Обладнання. Таблиця усних обчислень; картки для опитування; схеми задач. Зміст уроку І. Контроль, корекція і закріплення знань. 1. Перевірка домашнього […]...
- ПОРІВНЯННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 25. ПОРІВНЯННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ Із порівнянням раціональних чисел ви зустрічаєтесь чи не щодня. Наприклад, узимку, коли надворі мороз -15°, про температуру повітря кажуть, що вона менша від нуля: -15° < 0°. У відлигу, коли повітря прогрілося до +5°, кажуть, що температура стала більшою за нуль: +5° […]...
- ПОРІВНЯННЯ ПРЕДМЕТІВ ЗА РІЗНИМИ ОЗНАКАМИ. “СУСІДИ” ЧИСЛА. ФОРМУЛЮВАННЯ СУДЖЕНЬ “ЯКЩО…, ТО…”. ЗАПИСУВАННЯ НЕРІВНОСТЕЙ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 16. ПОРІВНЯННЯ ПРЕДМЕТІВ ЗА РІЗНИМИ ОЗНАКАМИ. “СУСІДИ” ЧИСЛА. ФОРМУЛЮВАННЯ СУДЖЕНЬ “ЯКЩО…, ТО…”. ЗАПИСУВАННЯ НЕРІВНОСТЕЙ Мета: ознайомити учнів з поняттям “сусіди” числа; вчити порівнювати предмети за різними ознаками, складати судження “якщо…, то…”, записувати нерівності; розвивати мовлення; виховувати інтерес до предмета. Хід уроку […]...
- Додатні та від’ємні числа Математика – Алгебра Раціональні числа Додатні та від’ємні числа Координатна пряма Пряма з вибраними на ній початком відліку, одиничним відрізком і вказаним додатним напрямом називається Координатною прямою. Число, що показує положення точки на координатній прямій, називається Координатою точки. Приклад Точка А розташована на прямій (див. рисунок) на відстані 2,5 одиничних відрізка праворуч від 0. Це […]...
- Раціональні числа; порівняння, додавання та віднімання. Розв’язування вправ Урок № 7 8 Тема. Раціональні числа; порівняння, додавання Та віднімання. Розв’язування вправ Мета: підготувати учнів до виконання тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь і навичок. Хід уроку I. Перевірка домашнього завдання @ Якщо на попередньому уроці не встигли зробити, то на початку цього уроку ми проводимо тестову роботу (з теми […]...
ВИБІРКА »