Тематична контрольна робота № 5
УРОК № 51
Тема. Тематична контрольна робота № 5
Мета уроку: контроль навчальних досягнень учнів з мети “Вектори”.
Тип уроку: комбінований.
Вимоги до рівня підготовки учнів: застосовують означення та властивості геометричних фігур при розв’язуванні задач.
Хід уроку
І. Тематичне оцінювання № 5
Тематичне оцінювання № 5 можна провести у вигляді тематичної контрольної роботи.
Наводимо текст контрольної роботи. Кожна правильна відповідь оцінюється в 3 бали.
Варіант 1
1. Знайдіть координати вектора
 – 2
– 2 , якщо
, якщо  (1; 1),
(1; 1),  (3; 1). 2. Дано три вершини паралелограма ABCD: A(-2; 1), В(-1; 1), С(1; 1). Знайдіть координати вершини D. 3. Дано вектори
(3; 1). 2. Дано три вершини паралелограма ABCD: A(-2; 1), В(-1; 1), С(1; 1). Знайдіть координати вершини D. 3. Дано вектори  (4; 2) і
(4; 2) і  (x; -4). При якому значенні х ці вектори колінеарні? 4. Трикутник ABC задано координатами його вершин: А(-1; 1), В(0; 2), С(1; 1). Знайдіть зовнішній кут при вершині А.
(x; -4). При якому значенні х ці вектори колінеарні? 4. Трикутник ABC задано координатами його вершин: А(-1; 1), В(0; 2), С(1; 1). Знайдіть зовнішній кут при вершині А.Варіант 2
1. Знайдіть координати вектора  = 2
= 2 –
–  , якщо
, якщо  (1; 1),
(1; 1), 
 (4; 2) і
(4; 2) і  (x; -4). При якому значенні х ці вектори перпендикулярні? 4. Трикутник ABC задано координатами його вершин: А(3; 5), В(4; 6), С(5; 5). Знайдіть зовнішній кут при вершині А.
(x; -4). При якому значенні х ці вектори перпендикулярні? 4. Трикутник ABC задано координатами його вершин: А(3; 5), В(4; 6), С(5; 5). Знайдіть зовнішній кут при вершині А.Варіант 3
1. Знайдіть координати вектора  =
=  – 3
– 3 , якщо
, якщо  (-1; 2),
(-1; 2),  (1; -2). 2. Дано три вершини паралелограма ABCD: A(-4; 1), В(-1; 3), D(-2; 1). Знайдіть координати вершини С. 3. Дано вектори
(1; -2). 2. Дано три вершини паралелограма ABCD: A(-4; 1), В(-1; 3), D(-2; 1). Знайдіть координати вершини С. 3. Дано вектори  (2; 5) і
(2; 5) і  (-6; у). При якому значенні у ці вектори перпендикулярні? 4. Трикутник ABC задано координатами його вершин: А(1; 3), В(2; 4), С(3; 3). Знайдіть зовнішній кут при вершині А.
(-6; у). При якому значенні у ці вектори перпендикулярні? 4. Трикутник ABC задано координатами його вершин: А(1; 3), В(2; 4), С(3; 3). Знайдіть зовнішній кут при вершині А.
Варіант 4
1. Знайдіть координати вектора  = 3
= 3 –
–  , якщо
, якщо  (-1; 2),
(-1; 2),  (1; -2). 2. Дано три вершини паралелограма ABCD: В(1; 3), С(-1;4), D(-2;2). Знайдіть координати вершини А. 3. Дано вектори
(1; -2). 2. Дано три вершини паралелограма ABCD: В(1; 3), С(-1;4), D(-2;2). Знайдіть координати вершини А. 3. Дано вектори  (2; 5) і
(2; 5) і  (-6; у). При якому значенні у ці вектори колінеарні? 4. Трикутник ABC задано координатами його вершин: А(0; 2), В(1; 3), С(2; 2). Знайдіть зовнішній кут при вершині А.
(-6; у). При якому значенні у ці вектори колінеарні? 4. Трикутник ABC задано координатами його вершин: А(0; 2), В(1; 3), С(2; 2). Знайдіть зовнішній кут при вершині А.
Відповіді та розв’язання до завдань тематичної контрольної роботи
Варіант 1
1.  (1 – 2 • 3; 1 – 2 • 1) =
(1 – 2 • 3; 1 – 2 • 1) =  (-5; -1). Відповідь.
(-5; -1). Відповідь.  (-5; -1).
(-5; -1).
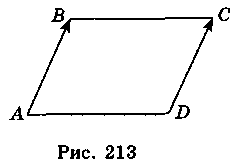
2. Нехай D(x; y), тоді 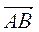 (1; 0),
(1; 0), 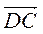 (1 – x; 1 – у) (рис. 213). Оскільки
(1 – x; 1 – у) (рис. 213). Оскільки 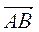 =
= 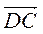 , то
, то 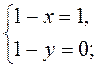
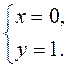 Отже, D(0; 1). Відповідь. D(0; 1).
Отже, D(0; 1). Відповідь. D(0; 1).
3. Вектори колінеарні, якщо 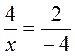 , тоді х = -16, х = -8. Відповідь. х = -8.
, тоді х = -16, х = -8. Відповідь. х = -8.
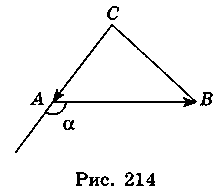
4. 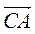 (-2; 0),
(-2; 0), 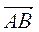 (1; 1) (рис. 214).
(1; 1) (рис. 214). 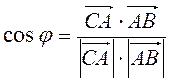 =
= 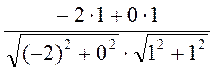 =
= 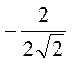 =
= 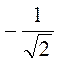 =
= 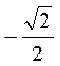 , звідси? = 135°. Відповідь. 135°.
, звідси? = 135°. Відповідь. 135°.
Варіант 2
1.  (2 • 1 – 3; 2 • 1 – 1) =
(2 • 1 – 3; 2 • 1 – 1) =  (-1; 1). Відповідь.
(-1; 1). Відповідь.  (-1; 1).
(-1; 1).
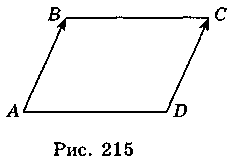
2. Нехай С(х; у), тоді 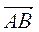 (1; 2),
(1; 2), 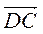 (х – 3; у + 3) (рис. 215). Оскільки
(х – 3; у + 3) (рис. 215). Оскільки 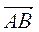 =
=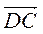 , то
, то 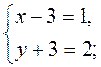
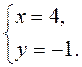 Отже, С(4; -1). Відповідь. С(4; -1).
Отже, С(4; -1). Відповідь. С(4; -1).
3. Дані вектори перпендикулярні, якщо 4 • х + 2 • (-4) = 0, тоді 4х – 8 = 0; 4х = 8; х = 2. Відповідь. 2.
4. 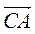 (-2; 0),
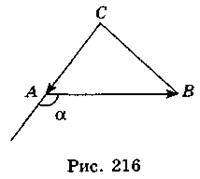
(-2; 0), 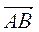 (1; 1), тоді (рис. 216)
(1; 1), тоді (рис. 216) 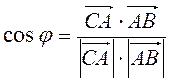 =
= 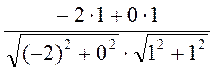 =
= 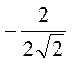 =
= 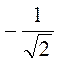 =
= 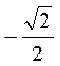 , звідси? = 135°. Відповідь. 135°.
, звідси? = 135°. Відповідь. 135°.
Варіант 3
1.  (-1 – 3 • 1; 2 – 3 • (-2)) =
(-1 – 3 • 1; 2 – 3 • (-2)) =  (-4; 8). Відповідь.
(-4; 8). Відповідь.  (-4; 8).
(-4; 8).
2. Нехай С(х; у), тоді 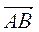 (3;2),
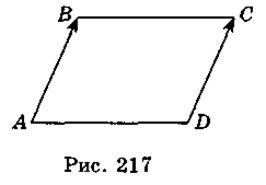
(3;2), 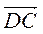 (x + 2; y – 1) (рис. 217). Оскільки
(x + 2; y – 1) (рис. 217). Оскільки 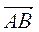 =
= 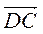 , то
, то 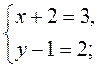
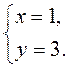 Отже, С(1; 3). Відповідь. С(1; 3).
Отже, С(1; 3). Відповідь. С(1; 3).
3. Дані вектори перпендикулярні, якщо 2 • (-6) + 5 • у = 0, звідси -12 + 5у = 0; 5у = 12; у = 2,4. Відповідь. 2,4.
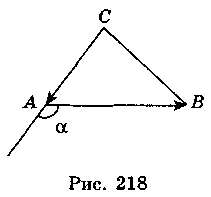
4. 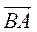 (-1; -1),
(-1; -1), 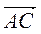 (2; 0) (рис. 218), тоді
(2; 0) (рис. 218), тоді
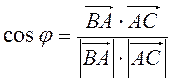 =
=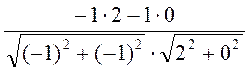 =
= 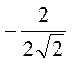 =
= 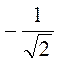 =
= 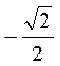 , звідси? = 135°. Відповідь. 135°.
, звідси? = 135°. Відповідь. 135°.
Варіант 4
1.  (3 • (-1) – 1; 3 • 2 – (-2)) =
(3 • (-1) – 1; 3 • 2 – (-2)) =  (-4; 8). Відповідь.
(-4; 8). Відповідь.  (-4; 8).
(-4; 8).
2. Нехай А(х; у), тоді 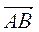 (1 – х; 3 – у),
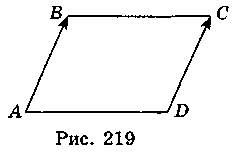
(1 – х; 3 – у), 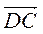 (1; 2) (рис. 219). Оскільки
(1; 2) (рис. 219). Оскільки 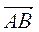 =
= 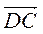 , то
, то 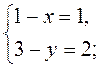
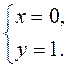 Отже, А(0; 1). Відповідь. А(0; 1).
Отже, А(0; 1). Відповідь. А(0; 1).
3. Вектори колінеарні, якщо 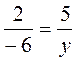 , звідси 2у = -30; у = -15. Відповідь. -15.
, звідси 2у = -30; у = -15. Відповідь. -15.
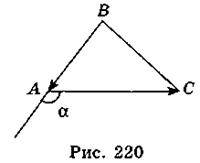
4. 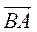 (-1; -1),
(-1; -1), 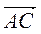 (2; 0) (рис. 220), тоді
(2; 0) (рис. 220), тоді
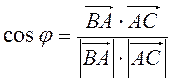 =
=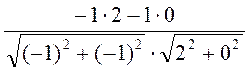 =
= 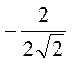 =
= 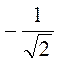 =
= 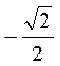 , звідси? = 135°. Відповідь. 135°.
, звідси? = 135°. Відповідь. 135°.
Тематичне оцінювання № 5 можна провести у вигляді тесту.
Тестова робота
Варіант 1
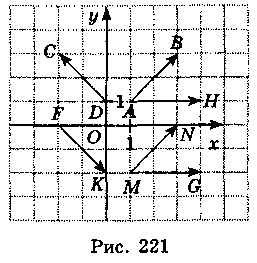
Користуючись рис. 221, виконайте завдання 1-6.
I рівень
1. Знайдіть координати вектора 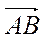 .
.
А. (1; 1); Б. (-2; 2); В. (2; 2); Г. (2; -2). 2. Укажіть координати вектора –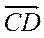 .
.
А. (-2; 2); Б. (2; -2); В. (2; 2); Г. (-2; -2).
3. Укажіть вектор, який дорівнює вектору 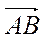 .
.
A. 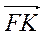 ; Б.
; Б. 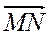 ; В.
; В. 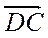 ; Г.
; Г. 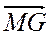 .
.
II рівень
4. Укажіть координати вектора 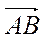 +
+ 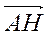 .
.
А. (2; 5); Б. (1; 2); В. (5; 2); Г. (1; -2).
5. Укажіть координати вектора 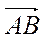 –
– 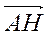 .
.
А. (1; 2); Б. (-1; 2); В. (1; -2); Г. (-1; -2).
6. Знайдіть 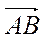 •
• 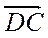 .
.
А.  ; Б. 2; В. 0; Г. 1.
; Б. 2; В. 0; Г. 1.
ІІІ рівень
7. При якому значенні вектори  (1; -1) і
(1; -1) і  (n; 1) колінеарні?
(n; 1) колінеарні?
А. Ні при яких n; Б. n = -1;
В. n = 1; Г. n = ±1.
8. При якому значенні п вектори  (1; 1) і
(1; 1) і  (n; 1) перпендикулярні?
(n; 1) перпендикулярні?
А. n = 1; Б. n = -1;
В. n = ±1; Г. ні при яких n.
9. Знайдіть координати вершини D паралелограма ABCD, якщо А(0; 2), В(1; 0), С(2; 0).
А. D(1; 2); Б. D(2; 2); В. D(1; -2); Г. D(2; 1).
IV рівень
10. Дано точки A(2; 1), B(3; 2), C(3; 1). Знайдіть внутрішній кут С трикутника ABC.
А. 30°; Б. 45°; В. 60°; Г. 90°.
11. Знайдіть площу чотирикутника ABCD, якщо А(0; 1), В(1; 3), С(2; 1), D(1; -1).
А. 2; Б. 4; В. 6; Г. 8.
12. Знайдіть кут А трикутника ABC, якщо А(0; 1), В( ; 2), С(
; 2), С( ; 1).
; 1).
А. 30°; Б. 45°; В. 60°; Г. 90°.
Варіант 2
Користуючись рис. 222, виконайте завдання 1-6.
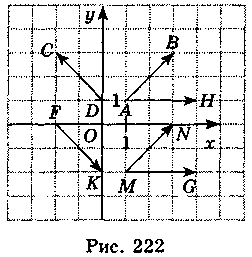
I рівень
1. Знайдіть координати вектора 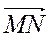 .
.
А. (1; 1); Б. (-2; 2); В. (2; 2); Г. (2; -2). 2. 2. Укажіть координати вектора –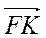 .
.
А. (-2; 2); Б. (2; -2); В. (2; 2); Г. (-2; -2). 3. Укажіть вектор, який дорівнює вектору 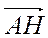 .
.
А. 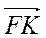 ; Б.
; Б. 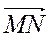 ; В.
; В. 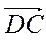 ; Г.
; Г. 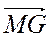 .
.
II рівень
4. Укажіть координати вектора 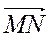 +
+ 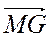 .
.
А. (2; 5); Б. (1; 2); В. (5; 2); Г. (1; -2).
5. Укажіть координати вектора 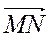 –
– 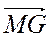 .
.
А. (1; 2); Б. (-1; 2); В. (1; -2); Г. (-1; -2).
6. Знайдіть 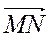 •
•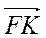 .
.
А.  ; Б. 2; В. 0; Г. 1.
; Б. 2; В. 0; Г. 1.
III рівень
7. При якому значенні п вектори  (-1; 1) і
(-1; 1) і  (п; -1) колінеарні?
(п; -1) колінеарні?
А. n = 1; Б. n = -1; В. n = ±1; Г. ні при яких n.
8. При якому значенні п вектори  (1; -1) і
(1; -1) і  (п; 1) перпендикулярні?
(п; 1) перпендикулярні?
А. Ні при яких n; Б. n = -1; В. n = 1; Г. n = ±1.
9. Знайдіть координати вершини А паралелограма ABCD, якщо В(1; 0), C(1; 1), D(-1; 0).
А. А(2; 1); Б. А(-1; -1); В. А(0; 1); Г. А(0; -1).
IV рівень
10. Дано точки A(1; 1), В(2; 1), С(2; 2). Знайдіть внутрішній кут А трикутника ABC.
А. 30°; Б. 45°; В. 60°; Г. 90°.
11. Знайдіть площу чотирикутника ABCD, якщо A(1; 1), В(2; 3), С(3; 1), D(2; -1).
А. 2; Б. 4; В. 6; Г. 8.
12. Знайдіть кут В трикутника ABC, якщо А(0; -1), В( ; 0), С(
; 0), С( ; -1).
; -1).
А. 30°; Б. 45°; В. 60°; Г. 90°.
Відповіді до тестових завдань
Рівень | Номер завдання | Варіант 1 | Варіант 2 |
І | 1 | В | В |
2 | А | А | |
3 | Б | Г | |
II | 4 | В | В |
5 | Б | Б | |
6 | В | В | |
III | 7 | Б | А |
8 | Б | В | |
9 | А | Б | |
IV | 10 | Г | Б |
11 | Б | Б | |
12 | А | В |
II. Домашнє завдання
Якщо в класі виконувалася тематична контрольна робота № 5, то вдома можна запропонувати тест, і навпаки.
III. Підбиття підсумків уроку
З’ясувати, які завдання викликали труднощі в учнів, та відповісти на запитання учнів.