Вектор. Модуль і напрям вектора. Рівність векторів
УРОК № 42
Тема. Вектор. Модуль і напрям вектора. Рівність векторів
Мета уроку: формування понять вектора, модуля вектора, напряму вектора; рівності векторів; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13].
Вимоги до рівня підготовки учнів: описують вектор, модуль і напрям вектора, рівність векторів; відкладають вектор, який є рівним даному; застосовують вивчені означення
Хід уроку
I. Перевірка домашнього завдання
Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли в учнів під час його виконання.
II. Аналіз результатів тематичної контрольної роботи №4
III. Сприймання й усвідомлення нового матеріалу
Вектором називають напрямлений відрізок. На рис. 188  – вектор, А – початок вектора, В – кінець вектора. Позначають вектор або двома великими буквами зі стрілкою (іноді з рискою) над ними, або однією маленькою буквою зі стрілкою (рискою).
– вектор, А – початок вектора, В – кінець вектора. Позначають вектор або двома великими буквами зі стрілкою (іноді з рискою) над ними, або однією маленькою буквою зі стрілкою (рискою).
Наприклад: 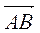
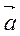 (рис. 188). У друкованому тексті букви, які позначають вектор, іноді виділяють напівжирним шрифтом, а стрілку (риску) зверху не ставлять.
(рис. 188). У друкованому тексті букви, які позначають вектор, іноді виділяють напівжирним шрифтом, а стрілку (риску) зверху не ставлять.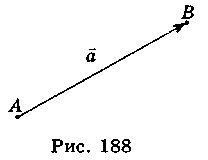
Довжиною (модулем, абсолютною величиною) вектора називається довжина напрямленого відрізка (позначення: 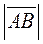 ,
, 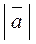 ).
).
Вектор, у якого початок збігається з кінцем, називається нульовим вектором. Позначення: 0. Довжина нульового вектора дорівнює 0: 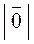 = 0.
= 0.
Ненульові вектори називаються колінеарними, якщо вони лежать або на одній прямій, або на паралельних прямих; нульовий вектор вважається колінеарним будь-якому ректору. На рис. 189 вектори 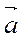 ,
, 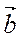 ,
, 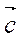 колінеарні.
колінеарні.
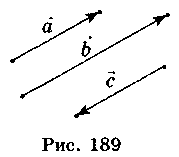
Одиничним вектором (ортом) називається вектор с, довжина якого дорівнює 1: 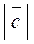 = 1.
= 1.
Ненульові вектори 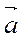 і
і 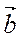 називаються однаково напрямленими, якщо вони колінеарні та напрямлені в один бік (рис. 189). Ненульові вектори die називаються протилежно напрямленими, якщо вони колінеарні та напрямлені в протилежні боки (рис. 189).
називаються однаково напрямленими, якщо вони колінеарні та напрямлені в один бік (рис. 189). Ненульові вектори die називаються протилежно напрямленими, якщо вони колінеарні та напрямлені в протилежні боки (рис. 189).
Вектори 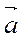 і
і 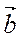 називаються рівними, якщо вони мають однакову довжину та однаково напрямлені (рис. 190).
називаються рівними, якщо вони мають однакову довжину та однаково напрямлені (рис. 190).
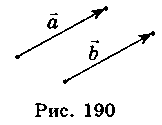
Вектори 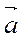 і
і 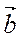 називаються протилежними, якщо вони мають однакову довжину та протилежно напрямлені (рис. 191). Вектор, протилежний вектору
називаються протилежними, якщо вони мають однакову довжину та протилежно напрямлені (рис. 191). Вектор, протилежний вектору 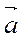 , позначають через –
, позначають через –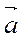 .
.
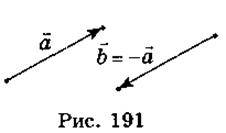
Теорема. Від будь-якої точки А можна відкласти вектор, що дорівнює даному вектору а, і притому тільки один.
Виконання вправ
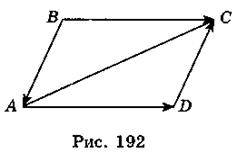
1. Укажіть однаково напрямлені, протилежно напрямлені вектори (рис. 192).
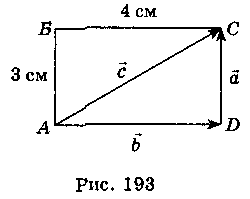
2. ABCD – прямокутник (рис. 193). Знайдіть 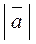 ,
, 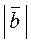 і
і 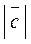 .
.
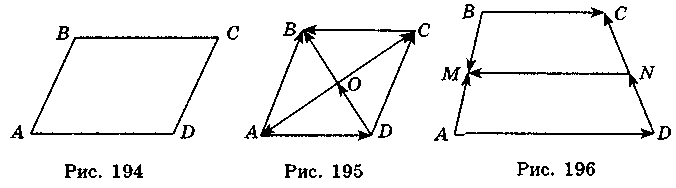
3. ABCD – паралелограм (рис. 194). Які векторні рівності можна записати? 4. Чи можлива рівність векторів 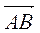 і
і 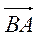 ? 5. Укажіть рівні і протилежні вектори, якщо на рис. 195 зображено ромб.
? 5. Укажіть рівні і протилежні вектори, якщо на рис. 195 зображено ромб.
IV. Закріплення й осмислення нового матеріалу
Розв’язування задач
1. ABCD – трапеція, MN – її середня лінія (рис. 196). Випишіть пари векторів, які мають:
А) однаковий напрям;
Б) протилежний напрям.
2. Діагоналі квадрата ABCD перетинаються в точці О. Запишіть вектори з початком і кінцем у вершинах квадрата або в точці О, які:
А) мають напрям, однаковий з вектором 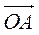 ;
;
Б) мають протилежний напрям з вектором 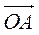 ;
;
В) дорівнюють вектору 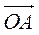 ;
;
Г) протилежні вектору 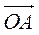 .
.
3. Точка В – середина відрізка АС, а С – середина відрізка BD. Чи рівні вектори:
А) 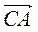 і
і 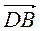 ?
?
Б)  і
і 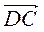 ?
?
4. У ромбі ABCD AC = 8 см, BD = 6 см. Знайдіть 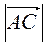 ,
, 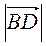 ,
, 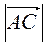
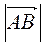 . 5. Скільки різних векторів задають усі можливі упорядковані пари точок, які є вершинами:
. 5. Скільки різних векторів задають усі можливі упорядковані пари точок, які є вершинами:
А) трикутника;
Б) чотирикутника?
V. Домашнє завдання
1. Вивчити теоретичний матеріал. 2. Розв’язати задачу.
У квадраті ABCD АВ = 2 см. Знайдіть 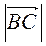 ,
, 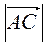 ,
, 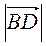 ,
, 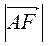 , де F – середина CD.
, де F – середина CD.
VI. Підбиття підсумків уроку
Заповніть пропуски в тексті.
Вектором називається…. Вектори  і
і 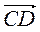 називаються однаково напрямленими, якщо промені АВ і CD… . Вектори
називаються однаково напрямленими, якщо промені АВ і CD… . Вектори  і
і 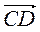 називаються…, якщо промені АВ і CD лежать у різних півплощинах відносно прямої АС і паралельні або лежать на одній прямій. Абсолютною величиною (або модулем) називається… . Вектор, початок якого збігається з кінцем, називається…. Рівні вектори мають… напрям і рівні…. Якщо вектори мають протилежні напрями і рівні модулі, то вони називаються….
називаються…, якщо промені АВ і CD лежать у різних півплощинах відносно прямої АС і паралельні або лежать на одній прямій. Абсолютною величиною (або модулем) називається… . Вектор, початок якого збігається з кінцем, називається…. Рівні вектори мають… напрям і рівні…. Якщо вектори мають протилежні напрями і рівні модулі, то вони називаються….