Головна ⇒ 📌Довідник з математики ⇒ Властивості числових нерівностей
Властивості числових нерівностей
Математика – Алгебра
Нерівності
Властивості числових нерівностей
a, b, с, d – довільні числа.
1. Якщо 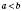 і
і 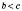 , то
, то 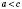 .
.
2. Якщо до обох частин правильної нерівності додати одне й те саме число, то дістанемо правильну нерівність.
3. Якщо обидві частини правильної нерівності помножити на одне й те саме додатне число, то дістанемо правильну нерівність. Якщо обидві частини правильної нерівності помножити на одне й те саме від’ємне число й змінити
4. Якщо
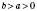 , то
, то 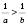 .
.5. Нерівності з однаковими знаками можна почленно додавати. Наприклад, якщо
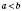 і
і 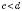 , то
, то 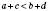 .
.6. Нерівності з однаковими знаками, у яких ліві й праві частини – додатні числа, можна почленно перемножувати. Наприклад, якщо a, b, с, d – додатні й
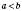 ,
, 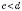 , то
, то 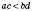 . Із цього випливає, що коли
. Із цього випливає, що коли 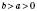 , n ∈ N,
, n ∈ N,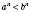 .
.Приклади
Відомо, що
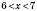 ,
, 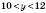 . Використовуючи властивості числових нерівностей, з’ясуйте, яких значень можуть набувати наведені вирази.
. Використовуючи властивості числових нерівностей, з’ясуйте, яких значень можуть набувати наведені вирази.а)
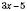 .
.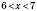 (за умовою),
(за умовою),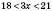 ,
, 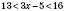 ;
;б)
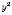 .
.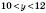 (за умовою),
(за умовою),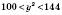 ;
;в)
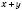 .
.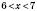 ,
, 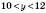 (за умовою),
(за умовою),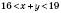 ;
;г)
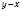 .
.Якщо
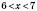 (за умовою), то
(за умовою), то 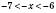 ,
,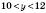 (за умовою),
(за умовою), 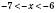 ,
, 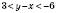 ;
;д) xy.
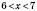 ,
, 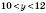 (за умовою),
(за умовою), 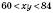 ;
;е)
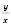 .
. Якщо
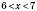 (за умовою), то
(за умовою), то 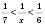 ,
, 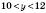 (за умовою),
(за умовою), 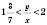 .
.Related posts:
- Основні властивості числових нерівностей УРОК № 4 Тема. Основні властивості числових нерівностей Мета уроку: домогтися засвоєння учнями змісту поняття “оцінити значення виразу”; закріпити знання учнів про зміст властивостей числових нерівностей та їхніх наслідків. Продовжити роботу з вироблення вмінь: відтворювати зміст вивчених властивостей, наслідків із них і їх доведення; застосовувати властивості числових нерівностей та наслідки з них для розв’язування вправ […]...
- Розв’язування нерівностей з однією змінною Математика – Алгебра Нерівності Розв’язування нерівностей з однією змінною Розв’язком нерівності з однією змінною називається значення цієї змінної, яке перетворює її на правильну числову нерівність. Розв’язати нерівність означає знайти всі її розв’язки або довести, що їх немає. Дві нерівності називають Рівносильними, якщо вони мають одні й ті самі розв’язки або не мають розв’язків. Числові проміжки […]...
- Числові нерівності. Доведення числових нерівностей УРОК № 2 Тема. Числові нерівності. Доведення числових нерівностей Мета уроку: домогтися засвоєння учнями змісту: додаткових нерівностей для суми взаємно обернених додатних чисел та середнього арифметичного двох невід’ємних чисел (у порівнянні з їх середнім геометричним) та доведення цих нерівностей; способу застосування доведених нерівностей при доведенні інших числових нерівностей. Продовжити роботу з вироблення вмінь: відтворювати зміст […]...
- Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання значення виразу УРОК № 6 Тема. Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання значення виразу Мета уроку: закріплення учнями змісту: властивостей числових нерівностей і теорем про почленне додавання та множення нерівностей; наслідків із властивостей числових нерівностей. Відпрацювання навичок: відтворювати зміст вивчених понять; застосовувати їх для розв’язування вправ: на порівняння виразів, на доведення нерівностей, […]...
- Числові та лінійні нерівності УРОК № 60 Тема. Числові та лінійні нерівності Тестові завдання 1. Яку подвійну нерівність задовольняє множина чисел, поданих на рисунку? А) -4 < x < 8; Б) -4 < х < 8; В) -4 < х < 8; Г) -4 < х < 8. 2. Відомо, що х < у. Яка з наведених нерівностей є […]...
- Системи нерівностей з однією змінною Математика – Алгебра Нерівності Системи нерівностей з однією змінною Розв’язком системи нерівностей з однією змінною називають значення змінної, яке є розв’язком кожної нерівності даної системи. Розв’язати систему нерівностей означає знайти всі її розв’язки або показати, що їх немає. Щоб розв’язати систему нерівностей, кожну її нерівність поступово спрощують, замінюючи рівносильною. Розглянемо на простих прикладах, як застосувати […]...
- Розв’язування показникових нерівностей УРОК 50 Тема. Розв’язування показникових нерівностей Мета уроку. Формування умінь учнів розв’язувати показникові нерівності. І. Перевірка домашнього завдання 1. Відповіді на запитання, що виникли в учнів при виконанні домашніх завдань. 2. Усне розв’язування показникових нерівностей з використанням таблиці 21 для усних обчислень “Показникові нерівності “. 1 2 3 4 5 1 2х > 8 2х […]...
- Розв’язування нерівностей, що містять показникову функцію УРОК 49 Тема. Розв’язування нерівностей, що містять показникову функцію Мета уроку. Познайомити учнів зі способами розв’язування показникових нерівностей. І. Перевірка домашнього завдання Відповіді на запитання, що виникли в учнів під час виконання домашніх завдань. II. Аналіз самостійної роботи, проведеної на попередньому уроці ІІІ. Сприймання і усвідомлення розв’язування найпростіших показникових нерівностей та тих, що безпосередньо зводяться […]...
- Розв’язування найпростіших тригонометричних нерівностей УРОК 29 Тема. Розв’язування найпростіших тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати найпростіші тригонометричні нерівності: tg t > a, tgt < a, ctg t < a, ctg t > a (tgt a, tgt a, ctg t a, ctg t a). І. Перевірка домашнього завдання 1. Відповіді на запитання, які виникли в учнів у процесі […]...
- Нерівності Математика – Алгебра Нерівності Число а вважається більшим від b, якщо різниця – число додатне. Число a менше від b, якщо різниця – число від’ємне. Якщо , то числа a і b рівні. На координатній прямій меншому числу відповідає точка, що лежить ліворуч від точки, яка відповідає більшому числу. Позначення: – a менше від b; […]...
- Розв’язування тригонометричних нерівностей УРОК 30 Тема. Розв’язування тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати тригонометричні нерівності. І. Перевірка домашнього завдання. 1. Відповіді на запитання, які виникли у учнів при виконанні домашнього завдання. 2. Фронтальна бесіда з учнями з використанням рис. 135. 1) Які дуги відповідають нерівностям: Tg t > a, tg t < a, tg t > […]...
- Числові послідовності. Властивості числових послідовностей УРОК № 49 Тема. Числові послідовності. Властивості числових послідовностей Мета уроку: домогтися засвоєння учнями змісту понять: числова послідовність, n-й член числової послідовності, формула п-го члена; списку способів задання числової послідовності. Виробити вміння: відтворювати вивчені означення; знаходити члени послідовності із заданими номерами, якщо послідовності задані різними способами. Повторити означення числової функції, а також супутні поняття. Тип […]...
- Розв’язування логарифмічних нерівностей УРОК 61 Тема. Розв’язування логарифмічних нерівностей Мета уроку. Формування умінь учнів розв’язувати логарифмічні нерівності І. Перевірка домашнього завдання Перевірити наявність виконаних домашніх завдань та відповісти на запитання, що виникли в учнів при виконанні цих завдань. II. Сприймання і усвідомлення розв’язування логарифмічних нерівностей (які розв’язуються введенням нової змінної) Приклад 1. Розв’яжіть нерівність log х – log5 […]...
- Нерівність з однією змінною. Система та сукупність нерівностей з однією змінною УРОК № 9 Тема. Нерівність з однією змінною. Система та сукупність нерівностей з однією змінною Мета уроку: засвоєння учнями змісту понять: нерівність з однією змінною, розв’язок нерівності з однією змінною та що означає розв’язати нерівність з однією змінною; система нерівностей з однією змінною, розв’язок системи нерівностей з однією змінною та що означає розв’язати систему нерівностей […]...
- Розв’язування ірраціональних нерівностей УРОК 39 Тема. Розв’язування ірраціональних нерівностей Мета уроку. Познайомити учнів з узагальненим методом інтервалів. Формування умінь розв’язувати ірраціональні нерівності. І. Перевірка домашнього завдання 1. Перевірити розв’язування вправ № 71 (3), 67 (1), 79 (1) за розв’язаннями на дошці, заготовленими до уроку. 2. Самостійна робота Розв’яжіть рівняння: А) = . (4 бали) Б) – = 2. […]...
- Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах2+bx+c. Розв’язування квадратних нерівностей” УРОК № 26 Тема. Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах 2 + b х + С. Розв’язування квадратних нерівностей” Мета уроку: повторити, систематизувати й узагальнити знання та вміння учнів щодо змісту вивчених у розділі “Функція та її властивості” понять і схем розв’язування типових задач шляхом складання загальних алгоритмів розв’язування задач. […]...
- Рівняння. Властивості рівносильності рівнянь Розв’яжіть задачі. 988. 1) 5х + 25 = 0; 5х = -25; х = -5; 2) 6у – 8 = 8; 6у = 16; у = 16/6; у= 3) 0,4x = 1,6; x = 1,6 : 0,4; x = 4; 4) 4у – 12 = 4; 4у = 16; y = 4. 989. 1) -2x […]...
- Лінійні нерівності та їхні системи УРОК № 61 Тема. Лінійні нерівності та їхні системи Тестове завдання 1. Знайдіть переріз проміжків (-6; 7] і (-4; 25]. А) [7; 25); б) [-4; 7); в) (-6; 25]; г) (-4; 7]. 2. Розв’яжіть нерівність . A) k < 1,125; б) k? ; в) k? 1,125; г) немає розв’язків. 3. При яких х має зміст […]...
- СКЛАДАННЯ І РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА МАЛЮНКОМ І СХЕМОЮ. ДОПОВНЕННЯ РІВНОСТЕЙ І НЕРІВНОСТЕЙ. РОЗПІЗНАВАННЯ ГЕОМЕТРИЧНИХ ФІГУР ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 55. СКЛАДАННЯ І РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА МАЛЮНКОМ І СХЕМОЮ. ДОПОВНЕННЯ РІВНОСТЕЙ І НЕРІВНОСТЕЙ. РОЗПІЗНАВАННЯ ГЕОМЕТРИЧНИХ ФІГУР Мета: навчати учнів складати і розв’язувати задачі на збільшення і зменшення числа на кілька одиниць за малюнком і схемою; закріплювати вміння доповнювати рівності і нерівності, розпізнавати геометричні фігури; вдосконалювати обчислювальні […]...
- ТАБЛИЦІ ДІЛЕННЯ НА 2 І 3. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ ЧИСЛОВИХ ВИРАЗІВ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ Мета: повторити прийоми складання таблиці ділення; розвивати вміння розв’язувати задачі, що містять дію ділення, знаходити значення числових виразів; розвивати логічне мислення; вдосконалювати обчислювальні навички; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання – Назвіть приклади з відповіддю 18; 21 і 27. 2. Гра “Допоможіть Сові розв’язати […]...
- Квадратна нерівність. Розв’язування квадратних нерівностей УРОК № 25 Тема. Квадратна нерівність. Розв’язування квадратних нерівностей Мета уроку: закріпити знання учнів про зміст означення квадратних нерівностей та схему їх розв’язування; удосконалити вміння учнів розв’язувати квадратні нерівності та нерівності, що зводяться до квадратних шляхом рівносильних перетворень, а також виробити вміння використовувати ці вміння під час розв’язування систем квадратних нерівностей та для розв’язування задач […]...
- Основні властивості рівнянь Математика – Алгебра Рівняння Два рівняння називають Рівносильними, якщо вони мають одні й ті ж корені; рівняння, які не мають коренів, також вважають рівносильними. Основні властивості рівнянь 1. Якщо виконати тотожні перетворення деякої частини рівняння, то одержимо рівняння, рівносильне даному. 2. Якщо деякий доданок перенести з однієї частини рівняння в іншу, змінивши при цьому його […]...
- Властивості десяткового дробу – Десяткові дроби Математика – Алгебра Десяткові дроби Властивості десяткового дробу Якщо до десяткового дробу дописати справа нуль (або декілька нулів), то дістанемо дріб, який дорівнює даному. Якщо десятковий дріб закінчується нулями, то ці нулі можна відкинути й дістанемо дріб, який дорівнює даному. Наприклад: ; ....
- Властивості нескінченно малих послідовностей Математика – Алгебра Границя Властивості нескінченно малих послідовностей Теорема 1. Алгебраїчна сума скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю. Послідовність називається Обмеженою, якщо існує таке число , що для всіх значень 2, … виконується нерівність . Теорема 2. Добуток нескінченно малої числової послідовності та обмеженої послідовності є нескінченно малою послідовністю. Послідовність називається Нескінченно […]...
- Зображення нерівностей земної поверхні на плані та карті Географія Загальна географія Земля на плані та карті Зображення нерівностей земної поверхні на плані та карті Усі нерівності земної поверхні називають Рельєфом. Щоб зобразити його на плані чи карті, необхідно виміряти висоту окремих ділянок земної поверхні. Для цього використовують нівелір. За його допомогою визначають, на скільки метрів вершина горба вища за його підошву. Цей процес […]...
- ПОРІВНЯННЯ ПРЕДМЕТІВ ЗА РІЗНИМИ ОЗНАКАМИ. “СУСІДИ” ЧИСЛА. ФОРМУЛЮВАННЯ СУДЖЕНЬ “ЯКЩО…, ТО…”. ЗАПИСУВАННЯ НЕРІВНОСТЕЙ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 16. ПОРІВНЯННЯ ПРЕДМЕТІВ ЗА РІЗНИМИ ОЗНАКАМИ. “СУСІДИ” ЧИСЛА. ФОРМУЛЮВАННЯ СУДЖЕНЬ “ЯКЩО…, ТО…”. ЗАПИСУВАННЯ НЕРІВНОСТЕЙ Мета: ознайомити учнів з поняттям “сусіди” числа; вчити порівнювати предмети за різними ознаками, складати судження “якщо…, то…”, записувати нерівності; розвивати мовлення; виховувати інтерес до предмета. Хід уроку […]...
- Розв’язування найпростіших тригонометричних нерівностей Математика – Алгебра Тригонометричні функції Розв’язування найпростіших тригонометричних нерівностей Найзручнішим є спосіб розв’язування тригонометричних нерівностей за допомогою тригонометричного кола. Приклади 1) . Побудуємо одиничне коло (див. рисунок нижче). Проведемо пряму . Вона перетинає коло у двох точках. Одна з них відповідає куту або , друга – куту або . Ці дві точки розбивають коло на […]...
- САНТИМЕТР. ВИМІРЮВАННЯ ДОВЖИНИ ВІДРІЗКІВ. ОБЧИСЛЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. ДОПОВНЕННЯ РІВНОСТЕЙ І НЕРІВНОСТЕЙ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 38. САНТИМЕТР. ВИМІРЮВАННЯ ДОВЖИНИ ВІДРІЗКІВ. ОБЧИСЛЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. ДОПОВНЕННЯ РІВНОСТЕЙ І НЕРІВНОСТЕЙ Мета: ознайомити учнів з одиницею вимірювання сантиметром та сантиметровою лінійкою; учити вимірювати довжину відрізка, доповнювати рівності і нерівності; закріплювати знання з нумерації чисел у межах 10; розвивати мислення; виховувати […]...
- РІВНЯННЯ. ОСНОВНІ ВЛАСТИВОСТІ РІВНЯНЬ Розділ 5 ВИРАЗИ І РІВНЯННЯ § 31. РІВНЯННЯ. ОСНОВНІ ВЛАСТИВОСТІ РІВНЯНЬ Ви вже знаете, що таке рівняння, корінь рівняння. Пригадаємо основні формулювання. Запам’ятайте Рівнянням називається рівність, що містить невідоме, значення якого треба знайти. Невідоме число в рівнянні позначають буквою х, або у, або z тощо. Наприклад, запис 4х + 7 = 15 є рівнянням, де […]...
- Логарифмічні нерівності Математика – Алгебра Логарифмічна функція Логарифмічні нерівності Розв’язуючи логарифмічні нерівності, спираються на такі твердження. 1. Якщо , то нерівність рівносильна подвійній нерівності . Це твердження можна записати у вигляді: або 2. Якщо , то нерівність рівносильна подвійній нерівності . Це твердження можна записати у вигляді: або Зверніть увагу: при розв’язуванні логарифмічної нерівності немає сенсу окремо […]...