Аксіоми стереометрії
Геометрія
Стереометрія
Аксіоми стереометрії
I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй.
Через будь-які дві точки можна провести пряму, й тільки одну.
II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими.
III. Кожний відрізок має певну довжину, більшу від нуля. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою.
IV. Пряма, що належить площині, розбиває цю площину на дві півплощини.
V. Кожний кут має певну градусну міру, більшу
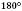. Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.VI. На будь-якій півпрямій від її початкової точки можна відкласти відрізок даної довжини, й тільки один.
VII. Від півпрямої на площині, що містить її, можна відкласти в задану півплощину кут із даною градусною мірою, меншою за
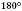, і тільки один.VIII. Який би не був трикутник, існує трикутник, що дорівнює йому, у даній площині в заданому розміщені відносно даної півпрямої у цій площині.
IX.
До цих аксіом додаються три аксіоми групи С.
. Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй.
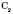. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку.
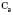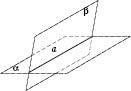
. Якщо дві різні прямі мають спільну точку, то через них можна провести площину, й до того ж тільки одну.Теорема 1. Через пряму і точку, яка не лежить на ній, можна провести площину, й до того ж тільки одну.
Теорема 2. Через пряму можна провести дві різні площини (див. рисунок).
Теорема 3. Якщо дві точки прямої належать площині, то вся пряма належить цій площині.
Отже, можливі три варіанти взаємного розміщення прямої і площини в просторі.
1. Пряма лежить у площині (рисунок зліва).
2. Пряма перетинає площину в даній точці (рисунок справа).
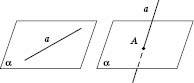
3. Пряма не перетинає площину (див. рисунок). У даному випадку Пряма А називається Паралельною площині.
Теорема 4. Через три точки, які не лежать на одній прямій, можна провести площину, й до того ж тільки одну.
Для розв’язання задач можуть бути корисними такі твердження.
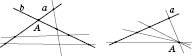
1. Якщо дві різні прямі перетинаються у деякій точці (рисунок нижче зліва), то всі прямі, які перетинають обидві дані прямі й не проходять через цю точку, лежать в одній площині.
2. Усі прямі, які перетинають дану пряму й проходять через дану точку поза прямою, лежать в одній площині (рисунок справа).
