Головна ⇒ 📌Довідник з геометрії ⇒ Декартові координати та вектори в просторі
Декартові координати та вектори в просторі
Геометрія
Декартові координати та вектори в просторі
Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок).
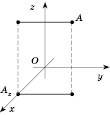
Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz.
Прямі Ox, Oy, Oz називаються Координатними осями (Ox – вісь абсцис, Oy – вісь ординат, Oz – вісь аплікат).
Точка їх перетину О – Початок координат, площини Oxy, Oxz, Oyz – Координатні
Точка О розбиває кожну з осей координат на дві півпрямі – півосі. Домовимось одну півось називати додатною, а другу – від’ємною.
Візьмемо тепер довільну точку А й проведемo через неї площину, паралельну площині Oyz. Вона перетинає вісь Ox у деякій точці
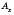 . Координатою Х точки А називається число, яке дорівнює за абсолютною величиною довжині відрізка
. Координатою Х точки А називається число, яке дорівнює за абсолютною величиною довжині відрізка 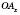 . Це число додатне, якщо точка
. Це число додатне, якщо точка 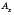 лежить на додатній півосі Оx, і від’ємне, якщо точка
лежить на додатній півосі Оx, і від’ємне, якщо точка 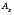 лежить на від’ємній півосі.
лежить на від’ємній півосі.Якщо точка
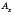
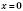 . Аналогічно означаємо координати y і z точки A. Координати точки записуватимемо в дужках поряд із буквеним позначенням точки:
. Аналогічно означаємо координати y і z точки A. Координати точки записуватимемо в дужках поряд із буквеним позначенням точки: 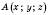 .
.Якщо точка A не належить жодній із координатних площин, то ці площини разом із трьома паралельними їм площинами, які проходять через точку А, обмежують прямокутний паралелепіпед.
Зверніть увагу на таке.
1)
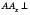 осі Oх;
осі Oх; 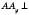 осі Oу;
осі Oу; 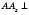 осі Oz (див. рисунок).
осі Oz (див. рисунок).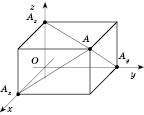
2)
Для розв’язування задач координатним методом користуються формулою
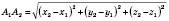 , що визначає відстань між точками
, що визначає відстань між точками 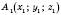 і
і 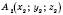 .
.
Нехай 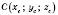 – середина відрізка AB, де
– середина відрізка AB, де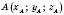 ,
, 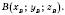 Тоді
Тоді 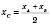 ;
; 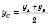 ;
; 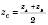 .
.
Related posts:
- Перетворення в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Перетворення в просторі Поняття перетворення для фігур у просторі означають так само, як і на площині (див. розділ “Геометрія. 8 клас”). Рухом Називається перетворення, при якому зберігаються відстані між точками. Властивості руху в просторі: Прямі переходять у прямі, півпрямі – у півпрямі, відрізки – у відрізки, кути між […]...
- Подібність просторових фігур – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Подібність просторових фігур Перетворення фігури F називається Перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюють себе в одну й ту саму кількість разів. Як і на площині, перетворення подібності в просторі переводить прямі у прямі, півпрямі у півпрямі, відрізки у відрізки і зберігає кути між півпрямими. […]...
- Декартові координати у просторі – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Декартові координати у просторі М – точка у просторі М(х, у, x) Мхy – проекція точки М на площину хоу; Мхy(х, о, у) Мх, Му, Mz – проекції точки М на осі OX, OY, OZ відповідно. Мх(х, о, о); Му(о, у, о); Мz(о, о, z). Відстань між точками А(x1,y1,z1) і […]...
- Вектори в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Вектори в просторі Усі основні означення векторів у просторі залишаються такими самими, як означення векторів на площині (див. розділ “Геометрія. 8 клас”). Координатами вектора , де , , називають числа, , . Вектори рівні тоді, й тільки тоді, коли вони мають відповідно рівні координати. Це дає підставу позначити […]...
- Прямокутна система координату просторі Урок 44 Тема. Прямокутна система координату просторі Мета уроку: знайомство з декартовою прямокутною системою координат у просторі. Обладнання: модель куба. Хід уроку І. Аналіз виконання тематичного оцінювання II. Перевірка домашнього завдання В кінці уроку збираються учнівські зошити для перевірки їх ведення й виконання домашнього завдання. III. Сприйняття й усвідомлення нового матеріалу Прямокутна система координат на […]...
- Координати і вектори у просторі 776. А(2; 0; 0), В(0; 0; 3), С(0; 5; -4), D(4; -3; 0), Е(2; 6; 4), F(6; -2; -6). 777. А(2; 0; 5), В(-4; 0; 2), С(4; 0; -2), D(1; 3; 1), A? хОz, В? xОz, C? xOz. Основа тетраедра ABC лежить у координатній площині хОz, Тому що yА = yB = yC = 0. […]...
- Вектори у просторі – ВЕКТОРИ Формули й таблиці МАТЕМАТИКА ВЕКТОРИ Вектори у просторі Вектор – спрямований відрізок А – початок вектора В – кінець вектора Модуль вектора – довжина відрізка, який зображує вектор: ||. Два вектори рівні, якщо вони однаково спрямовані і мають рівні модулі. Координати вектора з початком у точці А(x1,y1,z1) і кінцем у точці В(х2,у2,z2). Рівні вектори мають […]...
- Вектори і координати 74. 1) 2) B i C, A i D; 3 ) 4 ) 75. 76. I – паралелограм. 77. – паралелограм 80. 1) 2) 3) 81. 1) 2 ) 3) 4) 82. 1) φ = 60°. 2) φ = 180°, cos 180° = -1. 3) φ = 42°. 4) φ = 17°12′. 83. α ≈ […]...
- Перетворення симетрії в просторі. Симетрія в природі і на практиці Урок 47 Тема. Перетворення симетрії в просторі. Симетрія в природі і на практиці Мета уроку: формування знань учнів про перетворення симетрії в просторі та застосування знань до розв’язування задач. Обладнання: схема “Перетворення фігур”. Хід уроку І. Перевірка домашнього завдання 1. Усне коментування розв’язування домашніх завдань. 2. Математичний диктант. Дано трикутник АВС: Варіант 1 – А […]...
- Координати – Кінематика 5. Механіка 5.1. Кінематика 5.1.5. Координати Координати точки – це числа, які визначають положення фізичного тіла (матеріальної точки) на площині чи в просторі. В декартовій системі координат положення тіла (матеріальної точки) на лінії площини і в просторі визначається відповідно однією (а), двома (б) або трьома (в) координатами (X, Y, Z)....
- Вектори у просторі 156. ABCDEF – правильний шестикутник. А) Б) В) Але 157. 158. А) Б) В) 159. 160. А) Б) В) 161. 162. А(х; у; z). Тому -5 – х = З, x = -8; 4 – у = 4, у = 0; 1 – z = 2, z = -1. Отже, А(-8; 0; -1). 163. С(-2; […]...
- Координати середини відрізка УРОК № 23 Тема. Координати середини відрізка Мета уроку: виведення формул для знаходження координат середини відрізка та формування вмінь учнів застосовувати ці формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують та доводять формули координат середини відрізка. Застосовують вивчені формули […]...
- Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Урок 58 Тема. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Мета уроку: формування знань учнів про вектори в просторі, дії над векторами, заданими координатами, Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі”. Хід уроку І. Перевірка домашнього […]...
- Паралельне перенесення в просторі Урок 49 Тема. Паралельне перенесення в просторі Мета уроку: формування знань учнів про паралельне перенесення в просторі; вивчення його властивостей та застосування їх до розв’язування задач. Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 47), моделі куба і прямокутного паралелепіпеда. Хід уроку І. Перевірка домашнього завдання 1. Перевірити […]...
- Координати вектора УРОК № 43 Тема. Координати вектора Мета уроку: формування поняття координат вектора та вміння застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують координати вектора; застосовують вивчені означення і властивості до розв’язування задач. Хід уроку I. […]...
- Геометричні перетворення у просторі. Рухи 306. Пряма і площина відображуються на себе відносно будь-якої точки, що належить їм. 307. Два нерівні відрізки бути симетричними відносно деякої точки не можуть. 308. Відносно початку координат: Точці А(1; -3; 2) симетрична A1(-1; 3;-2); Точці В(-5; 0; 2) – B1(5; 0; -2); Точці С(3; -1; 0) – С1 (-3; 1; 0); Точці D(0; 0; […]...
- Розв’язування задач на знаходження кутів у просторі Урок 57 Тема. Розв’язування задач на знаходження кутів у просторі Мета уроку: формування вмінь учнів знаходити кути у просторі. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Два учні відтворюють розв’язування задач № 48 (2) 49 (1) на дошці. 2. Фронтальне опитування. 1) Сформулюйте теорему про площу ортогональної проекції многокутника. 2) Знайдіть площу ортогональної проекції […]...
- Рівняння сфери, площини і прямої 79. (x – 1)2 + у2 + (2 – 4)2 = 25. 80. A(10; 0; 0), В(0; 10; 0), С(0; 0; 10). 81. M(3; 2; -1) не належить сфері. X2+ у2 + z2 – 2х + 4у – 6z – 2 = 0, бо 32 + 22 + (-1)2 – 2 × 3 + 4 […]...
- Поняття про рух, рівність фігур у просторі Урок 48 Тема. Поняття про рух, рівність фігур у просторі Мета уроку: формування понять: рух, рівні фігури. Доведення нової властивості руху: площина під час руху переходить у площину. Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 48), модель куба. Хід уроку 1. Відповісти на запитання учнів, які виникли […]...
- Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин Урок 15 Тема. Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин Мета уроку: формування знань учнів про взаємне розміщення двох площин у просторі. Вивчення ознаки паралельності двох площин. Обладнання: стереометричний набір, схема “Взаємне розміщення двох площин”. Хід уроку 1. Перевірити наявність виконаних завдань та відповісти на запитання, які виникли в учнів під час […]...
- Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі УРОК № 53 Тема. Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі Мета уроку: повторити, привести в систему й розширити відомості про площину та взаємне розміщення двох площин у просторі; ознайомити учнів з різними випадками взаємного розміщення прямої і площини; дати уявлення про перпендикуляр до площини. […]...
- Координатна площина Математика – Алгебра Раціональні числа Координатна площина Проведемо дві перпендикулярні координатні прямі, які перетинаються в початку їх відліку – точці О. Ці прямі називаються Осями координат. Горизонтальну пряму називають Віссю абсцис І позначають Ox, вертикальну – Віссю ординат І позначають Oy. Точку О називають Початком координат. Ці координатні прямі утворюють Декартову прямокутну систему координат. Площина, […]...
- Координати середини відрізка Геометрія Декартові координати на площині Координати середини відрізка Якщо , – довільні точки, – середина відрізка AB, то ; ....
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...
- Взаємне розміщення прямих у просторі УРОК № 52 Тема. Взаємне розміщення прямих у просторі Мета уроку: повторити, привести в систему й розширити відомості про взаємне розміщення двох прямих у просторі. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]. Вимоги до рівня підготовки учнів: описують взаємне розміщення в просторі двох прямих; застосовують вивчені означення та властивості до розв’язування […]...
- Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Урок 13 Тема. Розміщення прямої і площини в просторі. Ознака паралельності прямої і площини Мета уроку: формування знань учнів про взаємне розміщення прямої і площини в просторі. Вивчення ознаки паралельності прямої і площини. Обладнання: стереометричний набір, моделі куба і тетраедра, схема “Аксіоми стереометрії”. Хід уроку І. Аналіз виконання тематичного оцінювання № 1. Зібрати зошити наприкінці […]...
- Перпендикулярність прямих у просторі Урок 25 Тема. Перпендикулярність прямих у просторі Мета уроку: формування поняття про перпендикулярні прямі. Вивчення теореми про прямі, що перетинаються і паралельні двом перпендикулярним прямим. Обладнання: стереометричний набір. Хід уроку В кінці уроку збираються учнівські зошити для перевірки їх ведення та виконання домашнього завдання. III. Сприйняття й усвідомлення нового матеріалу Означення перпендикулярних прямих у просторі […]...
- Вправи 1-49 1. А є ВС; В є АС. 2. А є с; В ∉ с. AB і с перетинаються в точці А. 3. Ці прямі мають тільки одну спільну точку А. 4. Точки В і С лежать по один бік від точки А. 5. а) Точка М лежить між L i N; Б) L і М […]...
- Тематичне оцінювання № 5 Урок 52 Тема. Тематичне оцінювання № 5 Мета уроку: перевірити навчальні досягнення учнів з теми “Декартові координати у просторі”. Хід уроку Тематичне оцінювання № 5 можна провести у вигляді тематичної контрольної роботи. 1. Тематична контрольна робота № 5 Варіант А 1. Чи лежать точки А, В, С на одній прямій, якщо А(1;1;-3), В (-1;3;5), С […]...
- Існування площини, яка проходить через дану пряму і дану точку УРОК 2 Тема. Існування площини, яка проходить через дану пряму і дану точку Мета уроку: вивчення теореми про існування площини, яка проходить через дану пряму і дану точку, що не лежить на прямій. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Фронтальна бесіда за контрольними запитаннями № 1, 2 §1 із підручника з […]...