Прямокутна система координату просторі
Урок 44
Тема. Прямокутна система координату просторі
Мета уроку: знайомство з декартовою прямокутною системою координат у просторі.
Обладнання: модель куба.
Хід уроку
І. Аналіз виконання тематичного оцінювання
II. Перевірка домашнього завдання
В кінці уроку збираються учнівські зошити для перевірки їх ведення й виконання домашнього завдання.
III. Сприйняття й усвідомлення нового матеріалу
Прямокутна система координат на площині розглядалась у попередніх класах. Кожній точці площини ставиться у відповідність
1. На координатній площині задано точки А, В, С, D, F, К (рис. 247). Визначте їх координати.
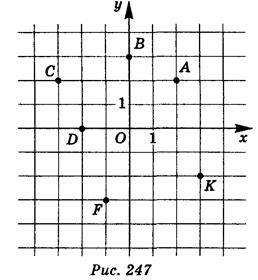
2. Побудуйте точки А (2; 3), B (-1; -2), C (0; -4), D (-3; 0).
Аналогічну систему координат можна ввести і для простору. Нехай х, у, z – три попарно перпендикулярні координатні прямі, які перетинаються в точці О (рис. 248 або рис. 68 із підручника). Ці координатні прямі називаються координатними осями: вісь х, вісь у, вісь z або вісь абсцис, вісь ординат, вісь аплікат відповідно,
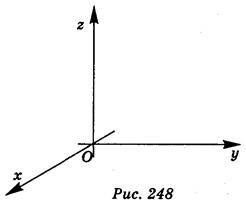
Кожна вісь точкою О розбивається на дві півосі – додатну, позначену стрілкою, і від’ємну.
Площини, які проходять через х і у, х і z, у і z, називають координатними площинами і позначають відповідно: ху, хz, уz. Координатні площини розбивають весь простір на вісім частин, які називають октантами. Візьмемо довільну точку А і проведемо через неї площину, паралельну уz (рис. 249). Вона перетинає вісь х у деякій точці А1. Координатою х точки А називається число, яке дорівнює за абсолютною величиною довжині відрізка ОА1; додатне, якщо точка А1 лежить на додатній півосі х, від’ємне, якщо вона лежить на від’ємній півосі і дорівнює нулю, якщо точка А, збігається з точкою О. Аналогічно позначаємо координати у і z точки А. Координати точки записуватимемо в дужках поряд із позначенням точки: А(х; у; z), інколи позначатимемо точку просто її координатами (х; у; z).
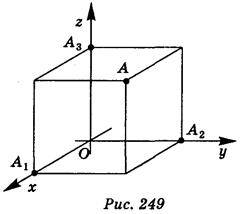
Якщо задано систему координат у просторі, то кожній точці простору можна поставити у відповідність три впорядковані дійсні числа х, у, z, і навпаки: кожній трійці чисел х, у, z – єдину точку простору.
Розв’язування вправ
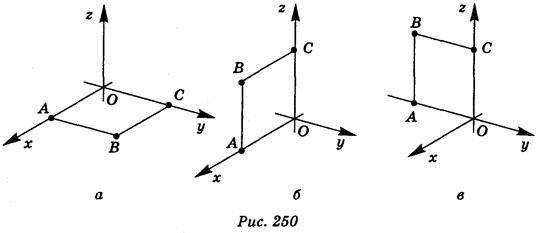
1. Сторона квадрата ОАВС дорівнює 5 (рис. 250). Знайдіть координати його вершин.
2. Сторона куба (рис. 251) дорівнює 10. Знайдіть координати його вершин.
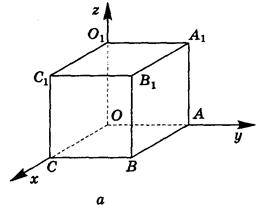
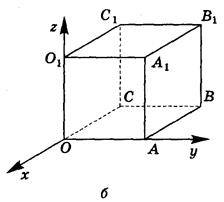
Рис. 251
3. Побудуйте точки А(1; 2; 3), В(3; -1; 3), C(1; 2; 0), F(0; 1, -2), Х(0; 0; -1).
4. Розв’язування задачі № 2 (с. 54) із підручника.
5. Запишіть координати точки А, якщо відомо, що вона розміщена:
А) на від’ємній півосі г на відстані 5 від початку координат;
Б) в площині ху на відстані 3 і 4 від осі х і у відповідно;
В) на відстані 3, 4, 5 від координатних площин ху, zх, zу відповідно;
Г) на відстані 3, 4, 5 від координатних осей х, у, z відповідно.
§4, п. 23; контрольне запитання № 1; задачі № 1, 3 (с. 54-55).
1) Поясніть, як позначаються координати точки в просторі.
2) Дано точку А (3; 2; 1). Укажіть координати основ перпендикулярів, опущених з цієї точки на координатні площини.
3) Дано точку А (3; 2; 1). Укажіть координати основ перпендикулярів, опущених з цієї точки на координатні осі.