Віднімання векторів
УРОК № 45
Тема. Віднімання векторів
Мета уроку: формування вмінь віднімати вектори, вивчення властивостей різниці векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13].
Вимоги до рівня підготовки учнів: описують віднімання векторів; відкладають вектор, що дорівнює різниці векторів; формулюють властивості різниці векторів; застосовують вивчені означення та властивості
Хід уроку
I. Перевірка домашнього завдання
Правильність виконання домашніх завдань перевірити за записами, зробленими на дошці до початку уроку, та відповісти на запитання, які виникли в учнів під час виконання домашніх завдань.
Математичний диктант
Дано точки:
Варіант 1
А(4; 5), В(1; 1).
Варіант 2
А(2; 3), В(-1; -1).
Запишіть:
А) координати вектора  ;
;
Б) координати вектора 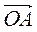 +
+ 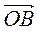 ;
;
В) довжину вектора  ;
;
Г) довжину вектора 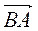 ;
;
Д) довжину
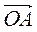 ;
;Є) довжину вектора 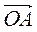 +
+ 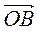 .
.
II. Сприймання й усвідомлення нового матеріалу
Різницею векторів  та
та  називається такий вектор
називається такий вектор  , сума якого з вектором
, сума якого з вектором  дорівнює вектору
дорівнює вектору  .
.
Різниця векторів  та
та  позначається так:
позначається так:  –
–  .
.
Різницю  –
–  векторів
векторів  та
та  можна замінити сумою вектора
можна замінити сумою вектора  з вектором, який є протилежним вектору
з вектором, який є протилежним вектору  , тобто
, тобто  –
–  =
=  + (-
+ (- ).
).
На рис. 203 подано два способи побудови різниці двох векторів  і
і  .
.
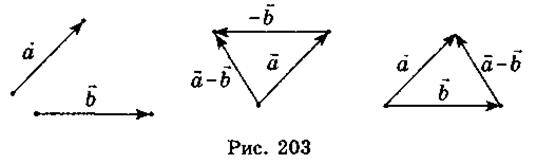
З означень додавання і віднімання двох векторів та властивостей трикутника випливають властивості модулів двох векторів:
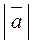 –
– 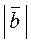 ?
? 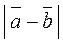 ?
? 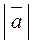 +
+ 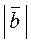 ,
, 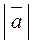 –
– 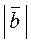 ?
? 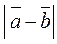 ?
? 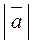 +
+ 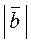 .
.
Координати різниці двох векторів дорівнюють різниці відповідних координат вектора-зменшуваного і вектора-від’ємника.
Якщо вектори задано на площині, то  (a1; a2) –
(a1; a2) –  (b1; b2) =
(b1; b2) =  (a1 – b1; a2 – b2).
(a1 – b1; a2 – b2).
Виконання вправ
1. Знайдіть вектор  , який дорівнює різниці векторів
, який дорівнює різниці векторів  і
і  , та абсолютну величину вектора
, та абсолютну величину вектора  , якщо:
, якщо:
А)  (4; 5) і
(4; 5) і  (1; 1);
(1; 1);
Б)  (2; 3) і
(2; 3) і  (-1; -1).
(-1; -1).
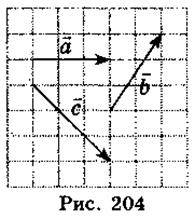
2. Накресліть у зошитах вектори  ,
,  ,
,  (рис. 204). Побудуйте вектор, який дорівнює:
(рис. 204). Побудуйте вектор, який дорівнює:
А)  –
–  ; б)
; б)  –
–  ; в)
; в)  –
–  ; г)
; г)  –
–  –
–  .
.
III. Закріплення й осмислення нового матеріалу
Розв’язування задач
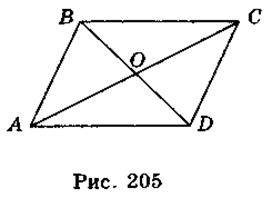
1. На рис. 205 зображено паралелограм ABCD. Запишіть вектор, який дорівнює різниці:
а)  –
– 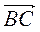 ; б)
; б)  –
– 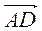 ; в)
; в) 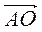 –
– 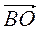 ; г)
; г) 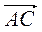 –
– 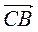 .
.
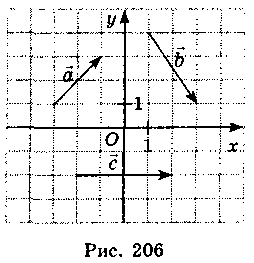
2. Знайдіть координати векторів (рис. 206):
А)  –
–  ; б)
; б)  –
–  ; в)
; в)  –
–  ; г)
; г)  –
–  –
–  .
.
3. Спростіть вираз:
А) 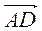 +
+ 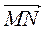 +
+ 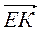 –
– 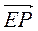 –
– 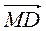 ;
;
Б) 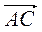 –
– 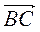 –
– 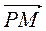 –
– 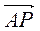 +
+ 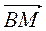 .
.
4. Дано: ABCD – паралелограм, О – довільна точка площини. Доведіть, що 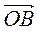 –
– 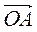 =
= 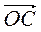 –
– 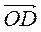 .
.
IV. Домашнє завдання
1. Вивчити теоретичний матеріал. 2. Розв’язати задачі.
1) Спростіть вираз:
A) ( –
– 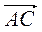 ) +
) + 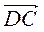 ;
;
Б) (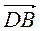 –
– 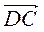 ) +
) + 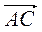 .
.
2) Дано: ABCD – паралелограм, О – довільна точка площини. Доведіть, що 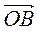 –
– 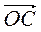 =
= 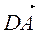 .
.
V. Підбиття підсумків уроку
Заповніть пропуски в тексті.
Щоб побудувати вектор  , який дорівнює
, який дорівнює  –
–  , досить додати вектори
, досить додати вектори  і… .
і… .
Щоб побудувати вектор  , який дорівнює
, який дорівнює  –
–  , треба відкласти ці вектори від однієї точки, тоді початок вектора
, треба відкласти ці вектори від однієї точки, тоді початок вектора  збігається з кінцем вектора…, а кінець вектора
збігається з кінцем вектора…, а кінець вектора  збігається з кінцем вектора…
збігається з кінцем вектора…
Для будь-яких трьох точок А, В, С справедлива рівність 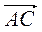 –
–  = … .
= … .