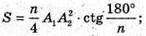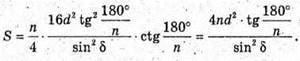Властивості піраміди

1.

1) Оскільки піраміда за своїми властивостями має парну кількість ребер, то піраміда не може мати 13 ребер.

2) З’ясуємо, чи має система розв’язки. 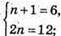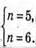Розв’язків не має.

Отже не існує піраміди, яка має 12 ребер і 6 граней.

2.

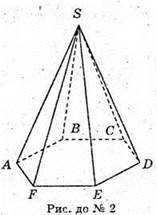
SABCDEF правильна шестикутна піраміда.

AB = BC = CD = DE = EE = AF = 6 cм. SA = SB = SC = SD = SE = SF = 5 cм.

Знайдемо площу бічної поверхні. Sбічн = SΔSFE

Розглянемо ΔSFE – рівнобедрений. Побудуємо SM + FE.

SM – висота і медіана, оскільки трикутник рівнобедрений.

Розглянемо

ΔSMF – прямокутний.

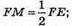FM = 3 см. З теореми Піфагора:

SM2 = SF2- FM2; SM2 = 52 – З2 = 16; SM = 4 см.

Тоді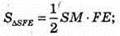

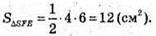
А отже Sбічн = 6 х 12 = 72 (см2).

3.

SABC – правильний тетраедр.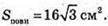

S повн = 4SΔACS отже 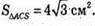ΔACS – правильний.

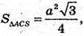Де а – довжина сторони трикутника.

Маємо: 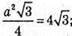а2 = 16; а = 4 см.

Отже, довжина ребра тетраедра 4 см.

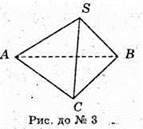
4.

SABCD – правильна чотирикутна піраміда;

AB = BC = CD = AD = 4 см;

SO – висота; SO = 6 см,

Знайдемо площу повної поверхні S повн = Sосн + S бічн; S бічн = 4SΔASD;

Sосн = AB2; SME = 42 = 16 (cм2).

ΔASD – рівнобедрений.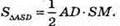

SM – знайдемо з прямокутного трикутника

SOM (∠SOM = 90º, оскільки SO – висота).

За теоремою Піфагора SM2 = MO2 + SO2,

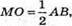МО= 2 cм. SM2 = 22 + 62 = 4 + 36 = 40;

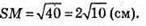Тоді

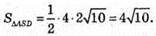
А отже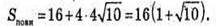

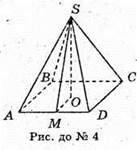
5.

SABCDSEF – правильна шестикутна піраміда.

SA = SB = SC = SO = SE = SF = 1 м.

∠ SAO = ∠ SВO = ∠ SCO = ∠SDO = ∠SEO = ∠ SFO = 45°.

Розглянемо трикутник SOA – прямокутний (SO + AO).

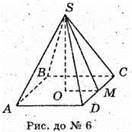
AO = AS • cos ∠ SAO;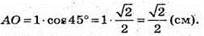

Розглянемо трикутник AOF – правильний.

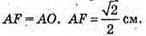
6.

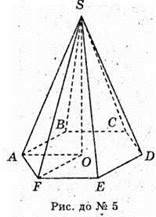
SABCD – правильна чотирикутна Піраміда;

SO – висота; SO = 3 см; ОМ + DC; SM + DC.

∠SMO – кут нахилу бічної грані до основи; ∠SMO = 45°.

Розглянемо ∠SOM – прямокутний (SO + ОМ).

ОМ = SO × ctg∠SMO; ОМ = 3 × ctg 45° = 3 × 1 = 3 (см).

AD = 2 × ОМ = 2 × 3 = 6 (см). Сторона основи дорівнює 6 см.

7.

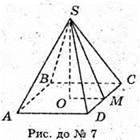
SABCD – правильна чотирикутна піраміда; SO – висота.

ОМ + DC; SM + DC. ∠SMO – кут нахилу бічної грані до площини основи;

∠SMO = 60°. SM – апофема.

SABCD = 16 см2. 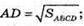AD = 4 см. 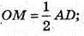ОМ = 2 см.

Розглянемо трикутник SOM – прямокутний (SO + ОМ).

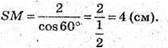
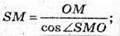
8.

SABCD – правильна чотирикутна піраміда; SO висота;

ОМ + DC; SM + DC. ∠SMO – кут нахилу бічної грані до площини основи;

∠SMO = 45°, SM — апофема,

AD = 3 см. Розглянемо трикутник SOM – прямокутний

(SO + ОМ), 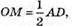ОМ = 1,5м.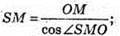

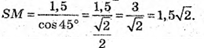
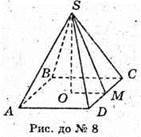
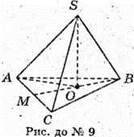
9. SABO – правильна трикутна піраміда. SO – висота; SM – апофема.

∠SMO = 30°. Знайдемо ∠ASC і ∠SAO. Позначимо ребро основи піраміди а.

ОМ – радіус вписаного кола.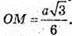

З трикутника SMO – прямокутного (SO + ОМ).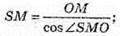

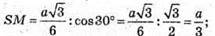
SO = МО × tg ∠SMO;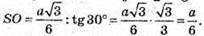

Розглянемо трикутник AMS – прямокутний (S2W + AC).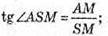

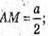
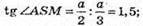
∠ ASM = arctg 1,5. Оскільки SM-медіана, то ∠ASC = 2∠ASM.

∠ASC = 2arctg 1,5. Розглянемо трикутник АОЗ – прямокутний.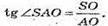

АО – радіус описаного кола.

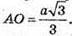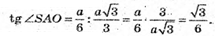Тоді А отже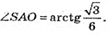

10.

SABC – правильна трикутна піраміда; SO – висота; SM апофема.

SM – 6 см. ОМ – радіус вписаного кола.

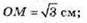
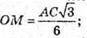
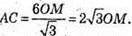
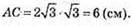
Знайдемо площу бічної поверхні. Оскільки піраміда правильна,

То Sбічн = 3 SΔACS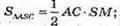

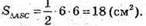
Отже S = 3 x 18 = 54 (см2).

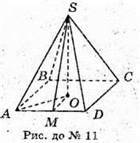
11.

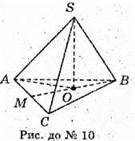
SABCD – правильна чотирикутна піраміда; SO – висота:

SM – апофема. АО – радіус описаного кола. 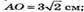SM = 10 см.

З трикутника АМО – прямокутного рівнобедреного:

AM = АО х cos ∠OAM;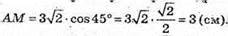

Оскільки SM – медіана, то АD = 2АМ, AD = 6 см.

Площа трикутника ASD.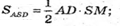

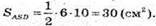Оскільки піраміда правильна, Sбічн = 4SΔASD;

Sбічн = 4 • 30 = 120 (см2).

12.

SABCD піраміда. ABCD – прямокутник. AB = DC = 6 cм; AD = ВС = 8 см.

(SАB) + (ABCD); (SBC) + (ABCD). ∠SDB – 60°. Знайдемо ∠SAB.

Розглянемо ΔSBD – прямокутний (SB + BD). SB = BD x tg ∠SDB.

BD знайдемо з трикутника BAD (∠BAD = 90°). За теоремою Піфагора

BD2 = АD2 + АB2. BD2 = 82 + 62 = 100; BD = 10 cм.

Тоді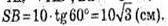

Розглянемо ΔABS – прямокутний (∠ABD = 90°).

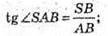
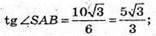
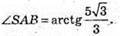
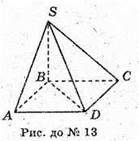
13.

SABCD – піраміда; ABCD – прямокутник. AB. = DC = 3 cм;

AD = BC = 4 cм. (ABS) + (ABCD); (BCS) + (A BCD). ∠ SAB = 30°.

Знайдемо ∠ SDB. Розглянемо трикутник ABC – прямокутний (AB + SB)

SB = AB x tg ∠SAB;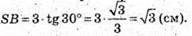

З прямокутного трикутника BAD (AB + AD) знайдемо за теоремою Піфагора BD:

BD2 = AB2 + AD2; BD2 = 32 + 42 = 25; BD = 5 cм.

Розглянемо прямокутний трикутник SBD (SB + BD).

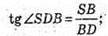
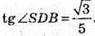Тоді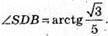

14.

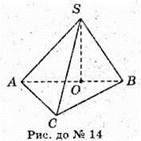
SABC – піраміда; ΔАСВ – прямокутний (∠ACB = 90°).

∠ABC = 30°; AC = 30 дм. ∠SAO = ∠SBO = ∠SCO = 60º,

SO – висота. Точка О – середина гіпотенузи.

Знайдемо довжину SO.

З прямокутного трикутника АСВ АВ = 2АС, АВ = 30 дм.

Тоді АО = 30 дм. Розглянемо трикутник AOS – прямокутний (SO + АВ).

SO = АО х tg∠SAO;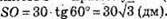

15.

SABCD – піраміда; ABCD – пpямокутник;

О – точка перетину діагоналей основи. SO – висота; SO = 4 cм.

∠ SMO та ∠ SKO – кути нахилу бічних граней до площини основи.

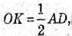
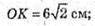
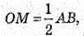
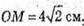
Розглянемо трикутник SOK – прямокутний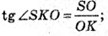

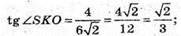
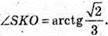
Розглянемо трикутник SOM – прямокутний.

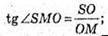
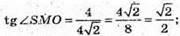
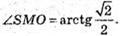
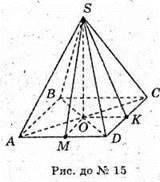
16. SABCD – правильна чотирикутна піраміда;

∠SMO = 45°; SO – висота; ОК – відстань від О до бічної грані;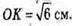

Розглянемо трикутник SOM – прямокутний, рівнобедрений

(оскільки ∠SMO = 45°, ∠MSO = 180° – 90° – 45° = 45°).

ОК є також і медіаною.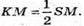

Розглянемо трикутник ОКМ – прямокутний.

(OK + SM). КМ = ОК х ctg∠KMO: ∠KMO = ∠SMO;

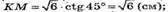
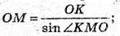
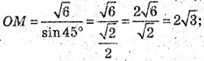
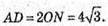
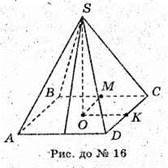
Розглянемо Δ SDC.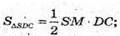

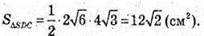
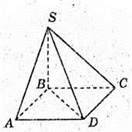
Оскільки піраміда правильна Sбічн = 4SΔSDC;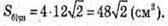

17.

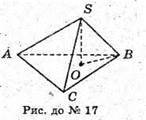
ABC – правильна трикутна піраміда; ∠ASC = ∠CSB = ∠ASB = 60°,

SO висота, SO = 4 см. Знайдемо Sбічн.

Оскільки ∠ASC = ∠CSB = ∠ASB = 60°,

То всі грані піраміди є правильними рівними трикутниками.

Позначимо ребро піраміди а. Розглянемо ∠SОВ – прямокутний.

З теореми Піфагора SO2= SB2 – OB2.

OB – радіус кола, описаного навколо правильного трикутника АВС.

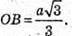Отже, маємо рівняння: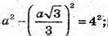

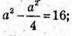
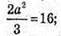
A2 = 24; 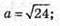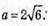Тоді =

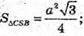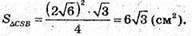
Площа бічної поверхні Sбічн =3SΔCSB;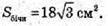

Відповідь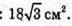

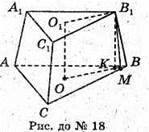
18.

ABCA1B1C1 – правильна зрізана трикутна піраміда. АВ = ВС = АС = 12 см.

A1B1 = В1С1 = А1С1 = 4 см. OO1 – висота піраміди.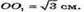

OB – радіуc кола, описаного навколо трикутника АВС.

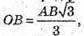
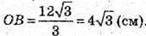
О1В1 – радіус кола, описаного навколо трикутника А1В1С1.

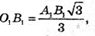
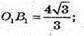ВК = ОВ – О1В1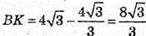

Розглянемо ΔB1КВ – прямокутний.

За теоремою Піфагора: ВВ21 = В1К2 + BК2;

В1К = ОО1;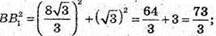

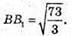
Розглянемо трапецію СС1В1В.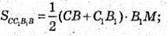

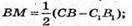
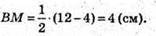
З трикутника В1МΒ — прямокутного: Β1М2 = BB21 – ВМ2;

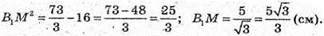
Тоді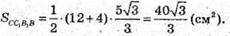

Оскільки піраміда правильна:

Sбічн = 3SCC1B1B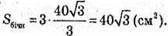

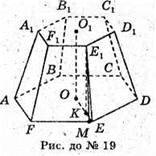
19.

Сторони основ правильної зрізаної піраміди FB = 4 см;

F1E1= 2 cм. OO1- висота піраміди;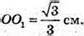

ОЕ = FE, O1E1 = F1E1; ОЕ = 4 см; O1E1 = 2 см; КЕ = ОЕ – О1Е1;

КЕ = 2 см;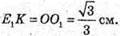

Розглянемо трикутник Е1КЕ – прямокутний.

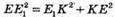– за теоремою Піфагора.

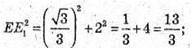
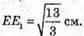
Розглянемо трикутник Е1ME – прямокутний (Е1Μ + ME).

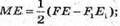
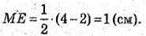
З теореми Піфагора: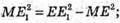

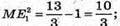
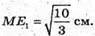
Тоді площа трапеції FF1E1Е: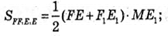

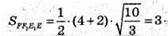
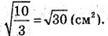
Sбічн = 6S FF1E1Е;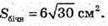

20.

АВСА1В1С1 – зрізана піраміда. ΔАСВ – прямокутний (∠ACB = 90°).

ΔΑ1С1Β1 – прямокутний (∠Α1С1Β1 = 90°). ∠CBA = ∠C1B1A1 = 30°.

АВ = 6 см; А1В1 = 4 см. СС1 висота піраміди,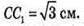

Знайдемо площу поверхні піраміди. Знайдемо площі кожної з граней.

Розглянемо трикутник АСВ – прямокутний.

СВ = АВ × cos∠CBA;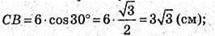

СА = АВ × sin∠CBA;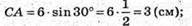

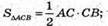
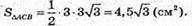
Розглянемо трикутник A1C1B1 – прямокутний,

С1В1 = А1В1 cos ∠С1В1А1;

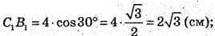С1А1 = А1В1 × sin∠C1B1A1;

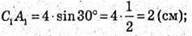
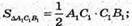
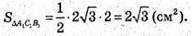СС1А1А – прямокутна трапеція.

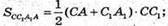
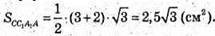
СС1В1В – прямокутна трапеція;

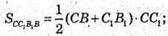
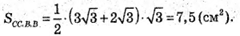
Розглянемо ΔΑ1КА – прямокутний (∠A1КA = 90º).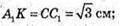

АК = СА – С1А1; АК = 3 – 2 = 1 (см).

За теоремою Піфагора: 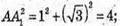АА1 = 2 см.

Розглянемо ΔΒ1ΜΒ – прямокутний (∠Β1ΜΒ = 90º).

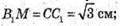ВМ = СВ – С1В1;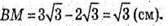

За теоремою Піфагора: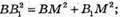

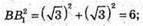
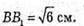
Розглянемо трапецію AA1B1B. А1N = В1Р – висоти трапеції.

Позначимо AM = х, тоді РВ = 6 – х – 4 = 2 – х.

З трикутника АNА1 – прямокутного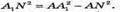

З трикутника В1РВ – прямокутного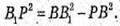

Маємо співвідношення: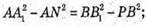

4 – x2 = 6 – (2 – x)2; 4 – x2 = 6 – 4 + 4x – х2; 4х = 2; х = 0,5.

Тоді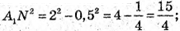

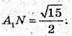
Обчислимо площу трапеції.

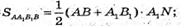
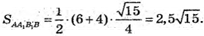
Тоді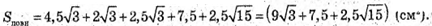

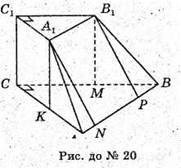
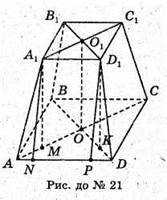
21.

ABCBA1B1C1B1 – зрізана піраміда; ABCD, А1В1С1D1 – ромби.

∠BAD = ∠B1A1D1 = 60°. АВ = 8 см; А1О1 = 6 см. ОО – висота,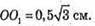

Знайдемо площу поверхні піраміди. S = Sповн = SABCD + SA1B1C1D1.

Розглянемо ΔAOD – прямокутний (∠AOD = 90°) AC1 – бісектриса кута BAD.

∠OAD = 30°. OD = AD × sin∠OAD;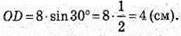

AO = AD × coS∠OAD;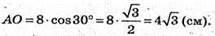

Розглянемо ΔΑ1Ο1D1 – прямокутний (∠A1O1D1 = 90°).

A1C1 – бісектриса кута. Β1Α1D1. ∠O1A1D1 = 30°.

O1D1 = A1D1 × sin∠O1A1D1;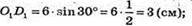

Α1Ο1 = A1D1 × cos∠O1A1B1;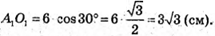

AC = 2AO; 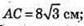BD = 2OD;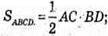

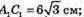
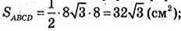
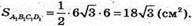
Розглянемо трикутник D1КD – прямокутний (D1К + ОD).

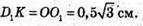DK = OD – O1D; DK = 4 – 3 = 1 (см).

За теоремою Піфагора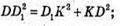

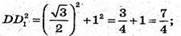
Розглянемо трикутник Α1МΑ – прямокутний (A1M + AО)

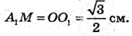AM = AO – A1О1;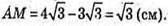

За теоремою Піфагора: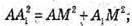

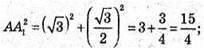
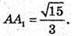
Розглянемо трапецію AA1D1D. AN = D1P – висоти.

Позначимо AN = x, тоді PD = 8 – x – 6 – 2 = 2 – x.

З прямокутного трикутника AM А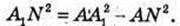

З прямокутного трикутника D1PD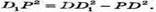

Маємо співвідношення: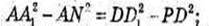

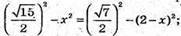
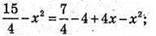
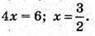
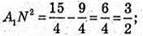
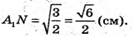
Обчислимо площу трапеції.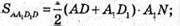

I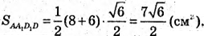

Тоді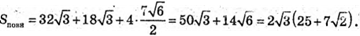

22.

SABCD – правильна чотирикутна піраміда; SO-висота, SO1 = OO1.

SA1B1C1D1 = 36см2. 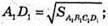А1D1 = 6 см.

Розглянемо трикутник ASD. Α1D1 – середня лінія трикутника. AD = 2А1D1;

AD = 2 × 6 = 12 (см).

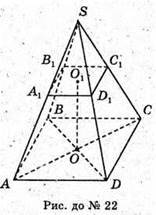
23.

SABCD – чотирикутна піраміда. ABCD – прямокутник; АВ = DС = 5см.

SA1B1C1D1 = 133см2. Розглянемо трикутник SDC. D1C1 – середня лінія трикутника.

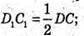D1C1 = 2,5 см. Знайдемо A1D1. A1B1C1D1 – прямокутник.

A1D1 = SA1B1C1D1 : D1C1; A1D1 = 133 : 2,5 = 53,2 (см). Розглянемо трикутник ASD.

Α1Β1 – середня лінія трикутника. AD = 2А1D1. AD = 2 × 53,2 = 106,4 (см).

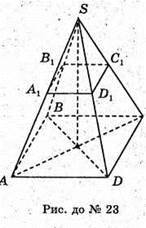
24.

Переріз паралельний основі відтинає на даній піраміді подібну їй піраміду.

Лінійні розміри цих пірамід відносяться як 2 : 1,

А отже площі будуть відноситися як 4 : 1.

Маємо: Sосн = 4Sпер та за умовами Sосн – Sпер = 381,

Звідси Sосн = 381 + Snep. Отримуємо 381 + Sпер = 4Sпер;

3Sпер = 381; Sпер = 127 см. Отже, Sосн = 508 см2.

26.

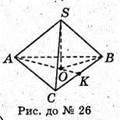
SABC – правильна трикутна піраміда.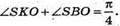

Нехай ребро основи дорівнює a; ∠SKO = α, тоді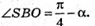

З трикутника SOK – прямокутного SO = OK × tg∠SKO.

OK – радіус вписаного кола.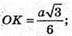

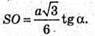
З трикутника SOB – прямокутного SO = ОВ × tg∠SBO.

ОВ – радіус описаного кола.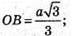

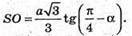
Отримуємо рівняння: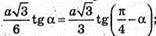

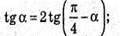
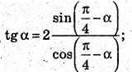
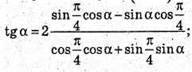
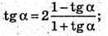
Tg2α + tgα = 2 – 2tgα; tg2α + 3tgα – 2 = 0;

D = b2 – 4ac = 9 – 4 × 1 × (-2) = 17;

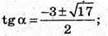
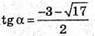– не підходить;

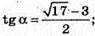
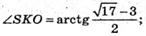
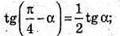
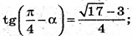
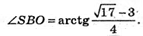
27.

SABC – правильна трикутна піраміда.

АО – радіус описаного навколо трикутника ASC, кола.

АО = R, ∠SAO = α. ΔABC – правильний.

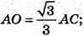
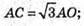
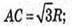
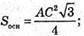
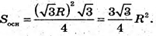
ОМ + АС. ОМ – радіус кола, вписаного в ΔАВС,

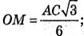
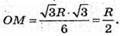
З трикутника SOA – прямокутного знайдемо SО.

SO = АО × tg∠SAO; SO = R tg α.

З трикутника SOM – прямокутного знайдемо SM.

За теоремою Піфагора

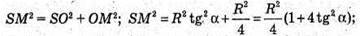
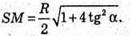
Знайдемо площу трикутника ASC.

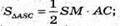
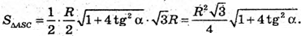
Повна поверхня піраміди

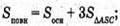
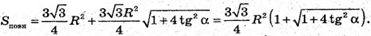
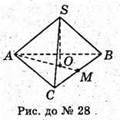
28.

SABC – правильна трикутна піраміда. АС = a; ∠SMO = α.

Трикутник ABC – правильний.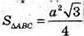

ОМ – радіус кола, вписаного в трикутник ABC.

З прямокутного трикутника SOM (∠SOM = 90º)

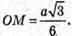
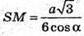
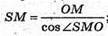
Знайдемо трикутника CSB.

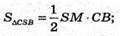
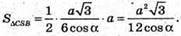
Знайдемо площу поверхні Sповн = Socн + 3SΔСSВ

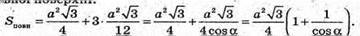
29.

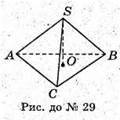
SABC – правильна трикутна піраміда.

∠CSB = α; AS = CS = BS = b. Розглянемо трикутник CSB.

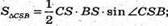
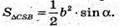
За теоремою косинусів СВ2 = CS2 + BS2- 2CS × BS × cos ∠CBS;

СВ2 = b2 + b2 – 2b × b × cosα = 2b2 – 2b2cosα = 2b2(1-cosα).

Трикутник ABC – правильний.

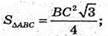
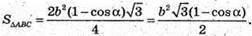
Знайдемо площу повної поверхні. Sповн = Socн + 3SΔCSB;

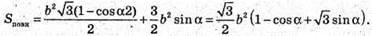
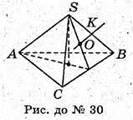
30.

SABC – правильна трикутна піраміда; ∠CSB = α, SO = R.

Точка О – точка перетину серединних перпендикулярів.

SM – медіана, бісектриса, висота.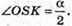

З трикутника SKO – прямокутного SK = SO × cas∠OSK;

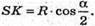
Тоді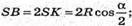 ВМ = SB sin ∠BSM;

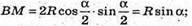СВ = 2ВМ; СВ = 2R sin α.

Трикутник ABC – правильний.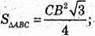

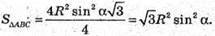
Площа трикутника CSB: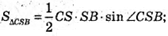

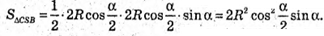
Визначимо площу повної поверхні.

Sповн = SΔABC + 3SΔCSB;

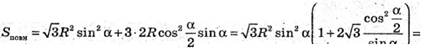
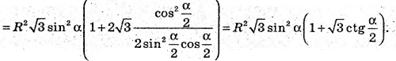
31.

SABCD – піраміда, ABCD – ромб;

∠BAD = α < 90º; AB = a; AК + DC; CK + DC; ∠SKA = β.

Розглянемо трикутник АКD – прямокутний.

∠ADK = ∠BAD = α; KD = AD × cos∠ADК;

КD = a x cos α; AК = AD × sin∠ADК; АК = а × sin α.

Розглянемо трикутник SAК – прямокутний (∠SAK = 90º).

SA = АК tg∠SBA; SК = a sin α tg β;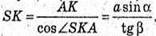

Розглянемо трикутник SAD.

За теоремою Піфагора SD2 = SA2 + ADZ;

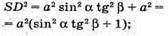
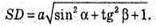
Знайдемо площу трикутника SAD.

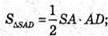
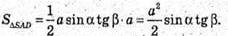
Знайдемо площу ΔSDC.

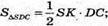
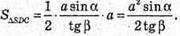
Знайдемо площу бічної поверхні. Sбічн = 2SΔSAD + 2SΔSDC;

Знайдемо площу бічної поверхні. Sбічн = 2SΔSAD + 2SΔSDC;

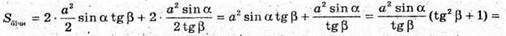
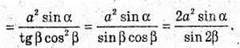
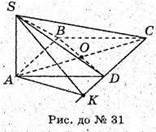
32.

SABCD – піраміда. ABCD – ромб;

∠BAD = α < 90º; ΑΚ + DC; SK + DC; ∠ SKA = β; AM = d.

Розглянемо трикутник AMK – прямокутний

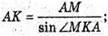
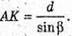
Розглянемо трикутник SAK – прямокутний.

SA = A К × tg ∠SKA;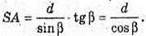

Розглянемо трикутник AКD – прямокутний.

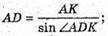
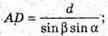∠ ADK = ∠BAD = α.

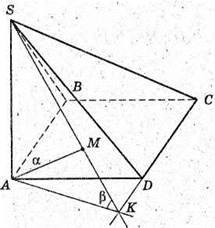
33.

SABCD – піраміда; ABCD – ромб;

∠ABC = β > 90°; AB + (ABCD). BL + DC; SL + DC;

∠SLB = α. SK = KB; KM + SL; KM = l.

Трикутник SBL – прямокутний (∠SBL = 90°).

∠BSL = 90° – ∠BLS = 90° – α.

Розглянемо трикутник SMK – прямокутний (∠SML = 90°).

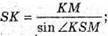∠KSM = ∠BSL;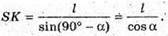

Оскільки SK = KB, то висота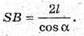

Розглянемо трикутник SBL – прямокутний (∠SBL = 90°).

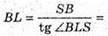
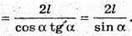
Розглянемо трикутник BLS – прямокутний (∠BLC = 90°).

∠BCL = 180° – β;

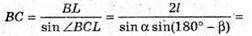
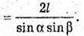
35.

1) SABC – правильна трикутна піраміда; ∠ASB = 30°.

Знайдемо ∠SKC. SO – висота піраміди.

Позначимо ребро основи a.

DK – радіус вписаного кола в трикутник ABC.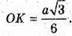

Розглянемо трикутник AKS – прямокутний (∠AKS = 90°).

Оскільки SK – висота, медіана та бісектриса трикутника ASB,

Маємо: 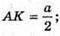∠ASK = 15°. Тоді SK = АК ctg∠ASK;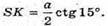

Розглянемо трикутник SOK – прямокутний (∠SOK = 90°),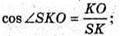

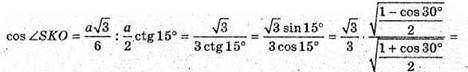
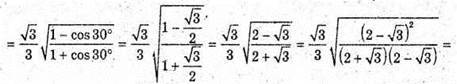
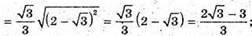
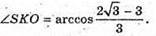
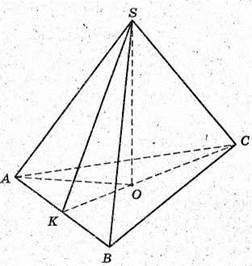
2) SABCD – правильна чотирикутна піраміда; ∠DSC = 30°.

SO – висота піраміди; SO + ABCD.

OK + DC; SK + DC. Знайдемо ZOKS.

Позначимо ребро основи а.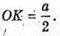

SK – висота, медіана, бісектриса трикутника DSC,

Значить ∠DSK = 15°.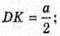

Розглянемо трикутник SKD – прямокутний (∠SKD = 90°).

SK = DK × ctg∠DSK;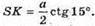

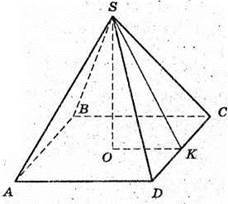
Розглянемо трикутник SOK – прямокутний (∠SOK = 90°),

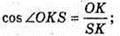
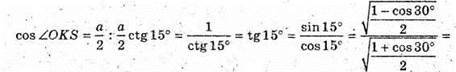
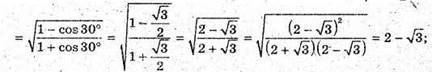
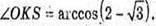
3) SABCDEF – правильна шестикутна піраміда;

∠ESD = 30°. SO – висота; SO + (ABCDEF). OK + ED; SK + ED.

Знайдемо ∠SKO. Позначимо ребро основи a.

SK – висота, медіана, бісектриса трикутника ESD,

Значить 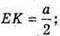∠ESK = 15°.

З трикутника ОКЕ – прямокутного (∠ΟΚΕ = 90°) ∠ΟΕΚ = 60°;

OK = ΕΚ × tg ∠OEK;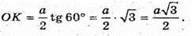

З трикутника SКА – прямокутного (∠SKE = 90°)

SK = ЕК × ctg ∠ESK;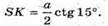

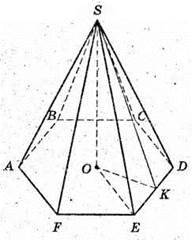
Розглянемо трикутник SPK – прямокутний

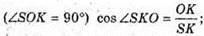
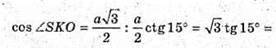
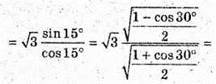
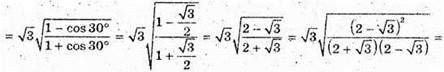
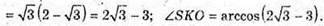
4) ∠A1SA2 = 30°. SO – висота; OK + А1А2; SK + А1А2. Знайдемо ∠OKS.

Розглянемо трикутник A1OA2.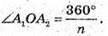

OК – висота, медіана, бісектриса трикутника А1ОА2.

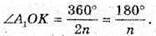
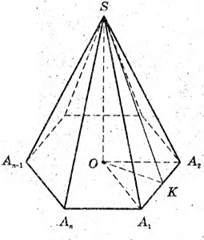
Позначимо довжину ребра основи а.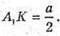

З трикутника ОКА1 – прямокутного (∠OKA = 90°) OK = А1К × ctg∠A1OK;

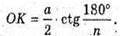
З трикутника SKA1- прямокутного (∠SKA1 = 90°) SK = Α1Κ × ctg∠Α1SΚ;

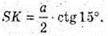
Розглянемо трикутник SOK – прямокутний (∠SOK = 90°).

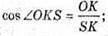
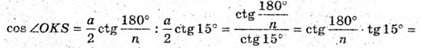
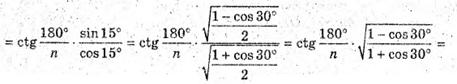
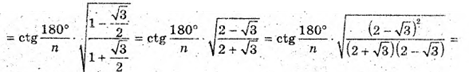
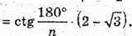
36.

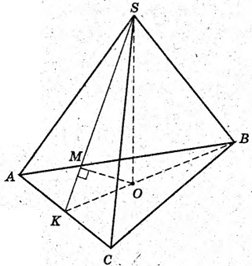
1) SABC – правильна трикутна пірамідa.

OS – висота; ВК + АС; SK + АС.

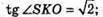АС = ВС =АС = 1 м.

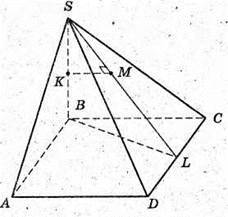
OМ + SК. Знайдемо ОМ.

ОК – радіус кола, вписаного в трикутник ABC.

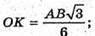
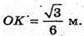
Розглянемо трикутник КМО – прямокутний (∠КМО = 90°).

МО = ОК × sin∠MKO; ∠МКО = ∠SKO;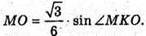

Скористаємось тим, що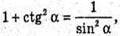

Тоді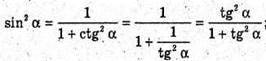

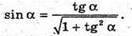
Маємо: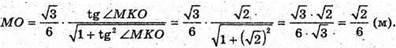

2) SABCD – правильна чотирикутна піраміда; OS – висота.

OK + DC; SK + X DC; 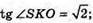AB = ВС = CD = AD = 1 м.

ОМ + SK. Знайдемо ОМ.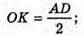

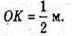
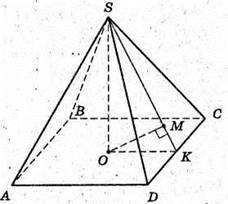
Розглянемо трикутник ОМК – прямокутний (∠ОМК = 90°).

МО = ОК × sin∠MKO; ∠МКО = ∠SKO.

Скористаємось тим, що 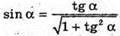(див. п. 1).

Маємо: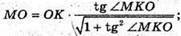

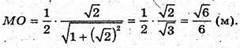
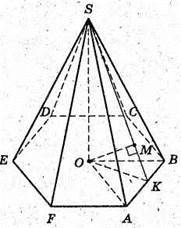
3) SABCDEF – правильна шестикутна піраміда; OS – висота;

OK + AB; SK + АВ;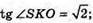

OK – радіус кола, вписаного в шестикутник ABCDEF.

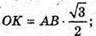
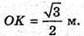
Розглянемо трикутник ОМК – прямокутний (∠ОМК = 90°).

МО = ОК × sin∠MKO; ∠МКО = ∠SKO.

Скористаємось тим, що (див. п. 1).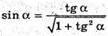

Маємо: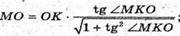

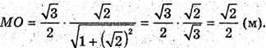
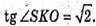
4) OS – висота; OK + А1А2; SK + А1А2

О К – радіус кола, вписаного в правильний n-кутник.

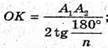
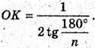
Розглянемо трикутник КМО – прямокутний (∠ΚΜΟ = 90°).

МО = OК × sin ∠МКО; ∠MKO = ∠SKO.

Скористаємось тим, що 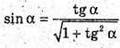(див. п. 1).

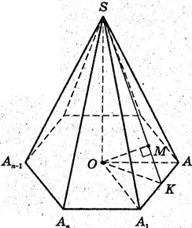
Маємо: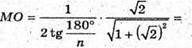

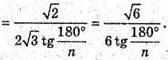
37.

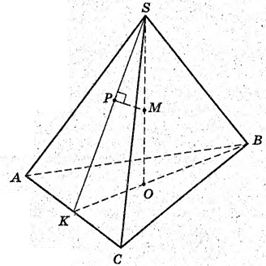
SABC – правильна трикутна піраміда; SO – висота; ОК = КS; КМ + SB;

КМ = 2 см. АР + ВС; SP + BC.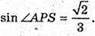

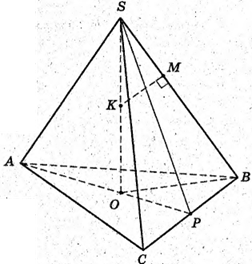
38.

1) SABC – правильна трикутна піраміда; SO – висота; OK + АС·, SK +АС;

∠SKO = δ. SM = МО. PM + SK; PM = d. ZSKO = δ, тоді ∠KSO = 90° – δ.

Розглянемо трикутник SPM – прямокутний (∠SPM = 90°).

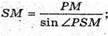
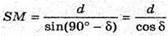Тоді SO = 2SM;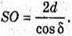

Розглянемо трикутник SOK – прямокутний (∠SOK = 90°).

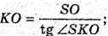
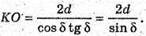
КО – радіус кола, вписаного в трикутник ABC.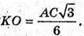

Тоді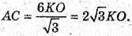

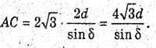
Тоді площа основи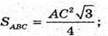

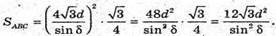
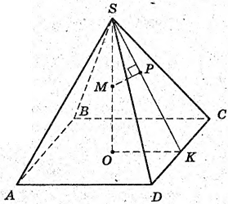
2) SABCD — правильна чотирикутна піраміда; SO – висота;

OK + DC; SK + DC, ∠SKO = δ. PM + SK; PM = d; SM = MO.

∠SKO = δ, тоді ∠KSO = 90° – δ.

Розглянемо трикутник SPM – прямокутний (∠SPM = 90°).

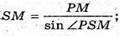
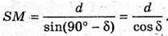
Тоді SO = 2SM;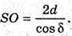

Розглянемо трикутник SOK – прямокутний (∠SOK = 90°).

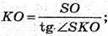
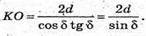
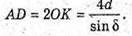
Тоді площа основи SABCD =AD2;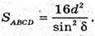

3) SABCDEF – правильна шестикутна піраміда; SO – висота;

ОК + АВ; SK + AB; ∠SKO=δ. PM + SK: PM = d; SM = MO.

∠SKO = δ, тоді ∠KSO = 90° – δ.

Розглянемо трикутник SPM – прямокутний

(∠SPM = 90°).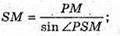

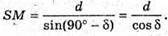
Тоді SO = 2SM;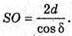

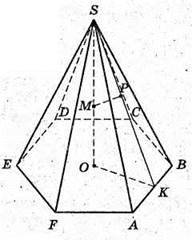
Розглянемо трикутник SOK – прямокутний (∠SOK = 90°).

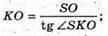
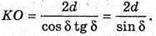
OK – радіус кола, вписаного в правильний шестикутник.

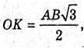Тоді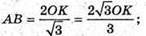

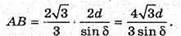
Площа основи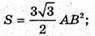

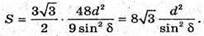
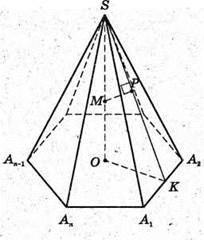
4) SO – висота; OK ∠ А1А2; SK + Α1Α2; ∠SKO = δ. PM + SK;

PM = d; SM = MO; ∠SKO = δ, тоді ZKSO = 90° – δ.

Розглянемо трикутник SPM – прямокутний (∠ SPM = 90°).

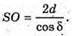
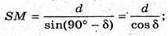
Розглянемо трикутник SOK – прямокутний (+ SOK = 90°).

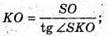
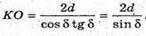
КО – радіус кола, вписаного в правильний n-кутник.

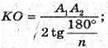
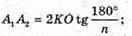
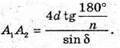
Тоді площа основи: