Розв’язування показникових рівнянь
УРОК 46
Тема. Розв’язування показникових рівнянь
Мета уроку. Формування умінь учнів розв’язувати показникові рівняння способом зведення до спільної основи; способом винесення за дужки спільного множника; способом зведення до спільного показника; графічним способом.
І. Перевірка домашнього завдання
Два учні на відкидних дошках відтворюють розв’язування вправ відповідно № 1, 3, 5, 7, 9 і № 2, 4, 6, 8, 10.
У цей час останні учні розв’язують рівняння № 48, 23.
№ 48: 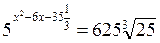 ;
; 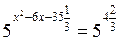 ;
;
X2 –
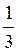 = 4
= 4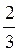 ; x2 – 6х – 40 = 0.
; x2 – 6х – 40 = 0.X1 = 10; х2 = – 4.
Відповідь: 10; – 4.
№ 23: 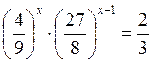 ;
; 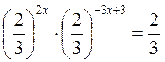 ;
; 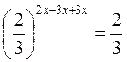 ;
;
2х – 3х + 3 = 1; – x = – 2; x = 2.
Відповідь: 2.
II. Набуття умінь розв’язувати показникові рівняння
Розглянемо деякі способи розв’язування показникових рівнянь.
1. Спосіб приведення рівняння до спільної основи, тобто до рівняння виду 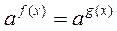 .
.
Як відомо, показникова функція у = ах, а > 0 і а? 1 монотонна, тому кожне своє значення вона приймає тільки при одному значенні аргументу. Із
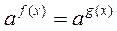 випливає, що f(x) = g(x).
випливає, що f(x) = g(x).Приклад 1. Розв’яжіть рівняння 2х – 5х = 0,1(10 х – 1)3.
2х – 5х = 0,1(10 х – 1)3; 10х = 10-1 – 103х – 3; 10х = 103х – 4; х = 3х – 4; х = 2.
Відповідь: 2.
2. Колективне розв’язування вправ із № 1 (17, 20, 49).
3. Спосіб винесення спільного множника за дужки.
Приклад 1. Розв’яжіть рівняння 3х – 2 – 3х – 2 = 63.
Розв’язання
3х – 2 – 3х – 2 = 63; 3х – 2(32 – 2) = 63; 3х – 2 – 7 = 63; 3х – 2 = 9; х – 2 = 2; х = 4.
Відповідь: 4.
Приклад 2. Розв’яжіть рівняння 52х – 1 – 52х + 22х + 22х + 2 = 0.
52х – 1 – 52х + 22х + 22х + 2 = 0;
22x(1+ 22) = 52х(1 – 5-1);
22х – 5 = 52х – 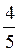 ;
;
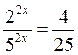 ;
; 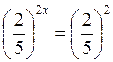 ; 2х = 2; x = l.
; 2х = 2; x = l.
Відповідь: 1.
4. Колективне розв’язування вправ із № 1 (22, 44).
5. Спосіб приведення рівняння до квадратного.
Приклад 1. Розв’яжіть рівняння 49х – 8 – 7х + 7 = 0.
49х – 8 – 7х + 7 = 0;
(72)x – 8 – 7х + 7 = 0;
(7х)2 – 8 – 7х + 7 = 0.
Нехай 7х = t, тоді t2 – 8t + 7 = 0; t1 = 7; t2 = 1.
Отже: 1) 7х = 7; х = 1; 2) 7х = 1; 7х = 70; х = 0.
Відповідь: 1; 0.
Приклад 2. Розв’яжіть рівняння (№ 1 (47)) 3 – 16х + 2 – 81х = 5 – 36х.
3 – 42x + 2 – 92x = 5 – 4х – 9х; 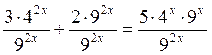 ;
; 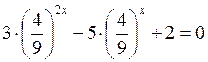 .
.
Заміна 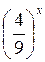 = у, тоді 3 y2 – 5y + 2 = 0, звідси y1 =
= у, тоді 3 y2 – 5y + 2 = 0, звідси y1 = 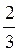 ; y2 = 1.
; y2 = 1.
Отже: 1) 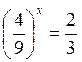 ;
; 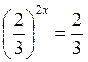 ; 2х = 1; х =
; 2х = 1; х =  ; 2)
; 2) 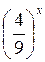 = 1; х = 0.
= 1; х = 0.
Відповідь: 0;  .
.
6. Колективне розв’язування рівнянь із № 1 (26, 32, 33).
7. Графічний спосіб розв’язування показникових рівнянь.
Приклад. Розв’яжіть графічно рівняння 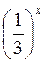 = х +1.
= х +1.
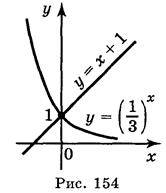
Будуємо графіки функцій у = 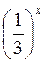 , у = х + 1 в одній системі координат. Графіки функцій у =
, у = х + 1 в одній системі координат. Графіки функцій у = 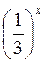 , у = х + 1 перетинаються в точці, абсциса якої х = 0 (рис. 154).
, у = х + 1 перетинаються в точці, абсциса якої х = 0 (рис. 154).
Відповідь: х = 0.
8. Розв’яжіть рівняння графічно:
А) 3х = 4 – х; б) 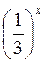 = х + 3; в) 4х = 5 – х; г) 3 – х = –
= х + 3; в) 4х = 5 – х; г) 3 – х = – 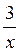 .
.
Відповідь: а) 1; б) -1; в) 1; г) -1.
IV. Домашнє завдання
Розділ IV § 2 № 31-34 із “Запитання і завдання для повторення”, № 1 (12, 13, 14, 15, 16).




 (1 votes, average: 5.00 out of 5)
(1 votes, average: 5.00 out of 5)Related posts:
- Розв’язування показникових рівнянь і систем показникових рівнянь УРОК 48 Тема. Розв’язування показникових рівнянь і систем показникових рівнянь Мета уроку. Формування уміння розв’язувати показникові рівняння і системи показникових рівнянь. І. Перевірка домашнього завдання 1. Чотири учні відтворюють розв’язування вправи № 1 (25, 28, 30, 46). 2. Усне розв’язування показникових рівнянь за допомогою таблиці 20 для усних обчислень “Показникові рівняння” 1 2 3 4 […]...
- Розв’язування показникових рівнянь і систем УРОК 47 Тема. Розв’язування показникових рівнянь і систем Мета уроку. Формування умінь учнів розв’язувати показникові рівняння і системи різними способами. І. Перевірка домашнього завдання. Три учні відтворюють на відкидних дошках розв’язування вправ: 1 учень – № 34 із “Запитань для повторення”; 2 учень – № 1 (12-14); 3 учень – № 1 (15, 16). У […]...
- Розв’язування показникових рівнянь, систем і нерівностей УРОК 51 Тема. Розв’язування показникових рівнянь, систем і нерівностей Мета уроку. Формування умінь розв’язувати показникові рівняння, системи і нерівності. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування вправи № 2 (11; 13; 16). 2. Колективне розв’язування нерівностей, аналогічних домашнім: вправи № 2 (30; 31). II. Аналіз самостійної роботи, проведеної на попередньому уроці III. Формування […]...
- Розв’язування систем логарифмічних рівнянь УРОК 59 Тема. Розв’язування систем логарифмічних рівнянь Мета уроку. Формування умінь учнів розв’язувати системи логарифмічних рівнянь. І. Перевірка домашнього завдання Проводиться колективне обговорення виконання домашніх вправ за записами розв’язання вправ № 52 (9; 11), 53 (12), 54 (2; 7), підготовленими до початку уроку. II. Самостійна робота Варіант 1 Розв’яжіть рівняння: А) lg(x2 – 2х) = […]...
- Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними УРОК № 30 Тема. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про зміст означень: графік рівняння з двома змінними, система рівнянь з двома змінними, розв’язок системи рівнянь з двома змінними, а також алгоритмів побудови графіка рівняння з двома змінними та графічного способу розв’язування системи […]...
- Розв’язування логарифмічних рівнянь УРОК 58 Тема. Розв’язування логарифмічних рівнянь Мета уроку. формування умінь учнів розв’язувати логарифмічні рівняння різними методами: зведення логарифмічного рівняння до алгебраїчного; метод потенціювання; зведення логарифмів до однієї і тієї самої основи; метод логарифмування та графічний метод. І. Перевірка домашнього завдання 1. Усне розв’язування логарифмічних рівнянь з використанням таблиці 24 для усних обчислень “Логарифмічні рівняння”. 1 […]...
- Розв’язування дробово-раціональних рівнянь УРОК 26 Тема. Розв’язування дробово-раціональних рівнянь Мета уроку: познайомити учнів з розв’язуванням дробово-раціональних рівнянь відносно тригонометричних функцій, формувати уміння учнів розв’язувати дробово-раціональні рівняння і проводити відбір коренів за допомогою одиничного кола. І. Перевірка домашнього завдання 1. Відповіді на запитання учнів, які виникли у них при виконанні домашнього завдання. 2. Розв’язування аналогічних вправ. Розв’яжіть рівняння: A) […]...
- Розв’язування систем тригонометричних рівнянь УРОК 27 Тема. Розв’язування систем тригонометричних рівнянь Мета уроку: познайомити учнів з окремими прийомами розв’язування систем тригонометричних рівнянь. І. Перевірка домашнього завдання 1. Чотири учні відтворюють розв’язування домашніх завдань: вправа № 2 (10; 18; 26; 38). 2. Усне розв’язування тригонометричних рівнянь, використовуючи таблицю “Тригонометричні рівняння”. 1 2 3 4 1 Sin x = 0 Cos […]...
- Розв’язування систем лінійних рівнянь із двома змінними способом додавання Урок № 76 Тема. Розв’язування систем лінійних рівнянь із двома змінним способом додавання Мета: сформувати в учнів усвідомлення необхідності знання алгоритму розв’язування лінійних рівнянь способом додавання та розуміння кожного кроку в цьому алгоритмі; виробити вміння використовувати названий алгоритм під час розв’язування систем лінійних рівнянь. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент […]...
- Розв’язування тригонометричних рівнянь способом розкладання на множники УРОК 24 Тема. Розв’язування тригонометричних рівнянь способом розкладання на множники Мета уроку: фрмування умінь учнів розв’язувати тригонометричні рівняння способом розкладання на множники. І. Перевірка домашнього завдання Перший учень пояснює розв’язування вправи № 2 (23), другий учень – вправи № 2 (30), третій – вправи № 2 (37). II. Сприймання і усвідомлення нового матеріалу Багато тригонометричних […]...
- Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції УРОК 23 Тема. Розв’язування тригонометричних рівнянь способом зведення до однієї тригонометричної функції Мета уроку: формування умінь учнів розв’язувати тригонометричні рівняння способом зведення до однієї тригонометричної функції (алгебраїчний спосіб). І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли у учнів при виконанні домашніх завдань. 2. Самостійна робота. Розв’яжіть рівняння: A) cosx = . (3 бали) […]...
- Системи лінійних рівнянь з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Системи лінійних рівнянь з двома невідомими Якщо треба знайти спільні розв’язки кількох рівнянь, то кажуть, що ці рівняння утворюють Систему рівнянь. Розв’язок системи рівнянь з двома невідомими – пара значень невідомих, яка є розв’язком кожного з рівнянь системи. Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що […]...
- СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ. ГРАФІЧНИЙ СПОСІБ РОЗВ’ЯЗАННЯ СИСТЕМ Цілі: – навчальна: сформувати поняття системи двох лінійних рівнянь з двома змінними, розв’язку системи двох лінійних рівнянь з двома змінними; сформувати вміння розв’язувати системи рівнянь графічним способом; – розвивальна: формувати вміння аналізувати інформацію; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, скрупульозність; Тип уроку : засвоєння нових […]...
- Розв’язування систем рівнянь з двома змінними УРОК № 33 Тема. Розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про різні способи розв’язування систем рівнянь з двома змінними та випадки їх застосування. Закріпити вміння: за видом системи визначати оптимальний спосіб її розв’язування, описувати дії відповідно до обраного способу розв’язування системи рівнянь з двома змінними, а також виконувати дії відповідно […]...
- Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Урок № 75 Тема. Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Мета: закріпити знання алгоритму розв’язування систем лінійних, рівнянь із двома змінними способом підстановки; вдосконалити вміння і навички, необхідні для застосування названого алгоритму; повторити матеріал попередньої теми щодо кількості розв’язків системи лінійних рівнянь залежно від співвідношення відповідних коефіцієнтів рівнянь. Тип уроку: засвоєння вмінь […]...
- Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 28. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Графічний спосіб розв’язування систем рівнянь є досить громіздким і до того ж не завжди допомагає знайти точні розв’язки. Розглянемо інші (не графічні) способи розв’язування систем лінійних рівнянь з двома змінними, які називають аналітичними. Почнемо зі способу […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg t = a УРОК 22 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg T = a. Мета уроку: зсвоєння учнями виведення і застосування формули для знаходження коренів рівняння tg t = a (ctg t = а). Обладнання: Таблиця “Рівняння tg t = а і ctg t = a”. І. Перевірка домашнього завдання 1. Перевірити наявність домашніх завдань в зошитах […]...
- Розв’язування однорідних тригонометричних рівнянь УРОК 25 Тема. Розв’язування однорідних тригонометричних рівнянь Мета уроку: формування умінь учнів розв’язувати однорідні тригонометричні рівняння. І. Перевірка домашнього завдання 1. Обговорення розв’язування вправи № 2 (6; 9; 11) за готовими розв’язаннями. 2. Розв’язування аналогічних вправ. А) 1 + cos x + cos 2x = 0; Б) cos4 x – sin4 x = ; В) […]...
- Розв’язування рівнянь графічним способом Математика – Алгебра Функції Розв’язування рівнянь графічним способом За допомогою графіків функцій можна розв’язувати рівняння графічним способом. Для цього треба побудувати в одній системі координат графіки обох частин рівняння й знайти абсциси точок їх перетину. Приклад. Розв’яжіть рівняння . Побудуємо графіки функції і в одній координатної системі (див. рисунок) і знайдемо абсиси точок їх перетину. […]...
- ПОВТОРЕННЯ. РОЗВ’ЯЗУВАННЯ РІВНЯНЬ І ЗАДАЧ Цілі: – навчальна: узагальнити та систематизувати знання учнів про види рівнянь, їх систем і способи їх розв’язання; – розвивальна: формувати вміння аналізувати й узагальнювати інформацію, бачити закономірності; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати відповідальність за результати своєї роботи, наполегливість у досягненні мети, віру у власні сили; Тип уроку : узагальнення та систематизація знань. […]...
- Розв’язування систем рівнянь Математика – Алгебра Розв’язування систем рівнянь Розглянемо системи рівнянь, в яких одне або обидва рівняння другого степеня. 1. Щоб розв’язати систему рівнянь графічним способом, треба побудувати в одній системі координат графіки обох рівнянь системи й знайти координати точок перетину графіків. Ці точки і будуть розв’язками системи рівнянь. Наприклад: Графіком першого рівняння є коло з центром […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos t = a УРОК 20 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos T = a Мета уроку: засвоєння учнями виведення і застосування формули для знаходження коренів рівняння cos t = a. Обладнання: Таблиця “Рівняння cos t = a”. І. Перевірка домашнього завдання Математичний диктант Обчисліть: 1) arcsin ; 2) arcos ; 3) arctg ; 4) arcsin; 5) arccos; […]...
- Розв’язування ірраціональних рівнянь, систем з ірраціональними рівняннями УРОК 38 Тема. Розв’язування ірраціональних рівнянь, систем з ірраціональними рівняннями Мета уроку. Формування умінь розв’язувати ірраціональні рівняння, системи з ірраціональними рівняннями. І. Перевірка домашнього завдання 1. Відповіді на запитання учнів, що виникли в процесі виконання домашніх завдань. 2. Фронтальна бесіда за питаннями № 49-53 із “Запитання і завдання для повторення” до розділу III. 3. Усне […]...
- Розв’язування систем лінійних рівнянь з двома змінними способом додавання Урок № 77 Тема. Розв’язування систем лінійних рівнянь з двома змінними способом додавання Мета: закріпити знання алгоритму розв’язання систем лінійних рівнянь із двома змінними способом додавання; відпрацювати вміння і навички, використання яких передбачено алгоритмом; ознайомити учнів із нестандартними задачами на застосування систем. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент 1. Перевірка […]...
- Система двох лінійних рівнянь із двома змінними та її розв’язок Урок № 72 Тема. Система двох лінійних рівнянь із двома змінними та її розв’язок Мета: сформувати уявлення учнів про розв’язок системи рівнянь із двома змінними та графічний спосіб розв’язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв’язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, […]...
- РОЗВ’ЯЗУВАННЯ ЛІНІЙНИХ РІВНЯНЬ Цілі: – навчальна: удосконалити вміння розв’язувати лінійні рівняння; формувати вміння розв’язувати рівняння зі змінною під знаком модуля та рівняння з параметрами, які зводяться до лінійних; – розвивальна: формувати вміння орієнтуватися в нестандартній ситуації; розвивати творчі здібності, кмітливість учнів; – виховна: виховувати наполегливість у досягненні мети, віру у власні сили, працьовитість; Тип уроку : удосконалення знань, […]...
- Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 23. Лінійне рівняння з однією змінною. Розв’язування лінійних рівнянь з однією змінною і рівнянь, що зводяться до них Ми знаємо, як розв’язувати рівняння 2х = -8; х – 5; 0,01х -17. Кожне із цих рівнянь має вигляд ах = b, де х – змінна, а і b […]...
- Розв’язування рівнянь та задач за допомогою рівнянь Урок № 105 Тема. Розв’язування рівнянь та задач За допомогою рівнянь Мета: підгодовувати учнів до виконання тематичної контрольної роботи. Тип уроку: узагальнення та систематизації знань. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання На окремих аркушах учні в завданнях 1 та 2 записують рівняння та його розв’язок; у завданні № 3 відповідь; після того […]...
- Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 29. Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Тепер розглянемо ще один аналітичний спосіб розв’язування систем двох лінійних рівнянь з двома змінними – спосіб додавання. Розв’язуючи систему способом додавання, ми переходимо від даної системи до рівносильної їй системи, одне з рівнянь якої містить лише […]...
- Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 27. Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Приклад 1. Маска й трубка для підводного плавання разом коштують 96 грн, причому маска на 16 грн дорожча за трубку. Скільки коштує маска і скільки трубка? Р о […]...
- Розв’язування тригонометричних рівнянь, систем та нерівностей УРОК 31 Тема. Розв’язування тригонометричних рівнянь, систем та нерівностей Мета уроку. Систематизувати навички і уміння розв’язувати тригонометричні рівняння, нерівності, системи. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування нерівностей із домашнього завдання. 2. Колективне розв’язування нерівностей: A) sin 2x sin x – cos 2x cos х . Sin 2x sin x – cos 2x […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = a УРОК 21 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = а Мета уроку: засвоєння учнями виведення і застосування формули для коренів рівняння sin t = а. Обладнання: Таблиця “Рівняння sin t = а”. І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли при виконанні домашніх завдань. 2. Самостійна робота. Варіант 1 Розв’яжіть рівняння: […]...
- Раціональні рівняння. Розв’язування раціональних рівнянь Урок № 21 Тема. Раціональні рівняння. Розв’язування раціональних рівнянь Мета: домогтися засвоєння учнями змісту схем розв’язання дробово-раціональних рівнянь із використанням основної властивості пропорції та властивості рівносильних рівнянь; закріпити знання учнів щодо вивчених на попередньому уроці понять (раціональне рівняння, ціле рівняння, дробово-раціональне рівняння, ОДЗ рівняння та схеми розв’язання дробового рівняння виду = 0, де А і […]...
- Розв’язання систем лінійних рівнянь способом підстановки Рівень А Відповідь: (1; 3). Відповідь: (7; -4,5). Відповідь: (1; 3). Відповідь: (4; 1). Відповідь: (3; 1). Відповідь: (1;-2). Відповідь: розв’язків немає. Відповідь: (3; 2). Відповідь: (4; 0). Відповідь: (3; 5). Відповідь: (1,5; 2). Відповідь: (3; -1). Відповідь: (7; 1). Відповідь: (1; -1). Рівень Б Відповідь: (2; 1,5). Відповідь: (1; -2). Відповідь: (20; 0,5). Відповідь: […]...
- Розв’язування лінійних рівнянь з однією змінною Урок № 99 Тема. Розв’язування лінійних рівнянь з однією змінною Мета: закріпити знання учнів про властивості рівносильності рівнянь та способи їх застосування для розв’язування лінійних рівнянь з однією змінною; вдосконалити вміння учнів розв’язувати лінійні рівняння з однією змінною з використанням зазначених вище знань. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент II. […]...
- Найпростіші ірраціональні рівняння УРОК 37 Тема. Найпростіші ірраціональні рівняння Мета уроку. Познайомити учнів з методами розв’язування ірраціональних рівнянь. Формування умінь розв’язувати ірраціональні рівняння. І. Перевірка домашнього завдання 1. Фронтальна бесіда за запитаннями № 38-46 із “Запитання і завдання для повторення до розділу III”. 2. Розв’язування вправ, аналогічних до домашніх. А) Обчислити . Відповідь: 3. Б) Обчислити . Відповідь: […]...
- Розв’язування логарифмічних рівнянь Математика – Алгебра Логарифмічна функція Розв’язування логарифмічних рівнянь Логарифмічними рівняннями називають такі рівняння, які містять змінну під знаком логарифма. Найпростішим логарифмічним рівнянням є , де , . Корінь цього рівняння дорівнює . Рівняння , де , , рівносильне системі: Зверніть увагу: у цій системі можна випустити одну з нерівностей. Із цього випливає, що для розв’язання […]...
- Логарифмічні рівняння УРОК 57 Тема. Логарифмічні рівняння Мета уроку. Формування умінь учнів розв’язувати логарифмічні рівняння. І. Перевірка домашнього завдання 1. Фронтальна бесіда за № 15-25 із “Запитання і завдання для повторення” розділу V та відповіді на запитання, які виникли в учнів у процесі виконання домашніх завдань. 2. Виконання вправ, аналогічних домашнім: № 47 (1; 3), 51. II. […]...
- Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Урок № 73 Тема. Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Мета: засвоїти знання щодо залежності кількості розв’язків системи лінійних рівнянь від співвідношення коефіцієнтів a, b, c цих рівнянь; вироблення вмінь застосовувати названу ознаку під час графічного розв’язання систем рівнянь; подальше вдосконалювати вміння розв’язувати системи лінійних рівнянь графічним способом. Тип […]...
- Основні властивості рівнянь Математика – Алгебра Рівняння Два рівняння називають Рівносильними, якщо вони мають одні й ті ж корені; рівняння, які не мають коренів, також вважають рівносильними. Основні властивості рівнянь 1. Якщо виконати тотожні перетворення деякої частини рівняння, то одержимо рівняння, рівносильне даному. 2. Якщо деякий доданок перенести з однієї частини рівняння в іншу, змінивши при цьому його […]...