Симетрія відносно площини
334.
Якщо відрізок належить площині α, то відрізок симетричний сам собі.
Якщо відрізок не лежить в площині:
А)
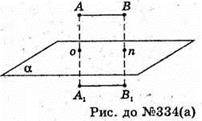
Відрізок паралельний площині α
АА1 + α; АО = ОА 1
ВВ1 + α; BN = NB,
A1В1 симетричний АВ відносно α;
Б)
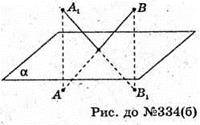
Відрізок перетинає площину α.
Відрізок А1В1 симетричний відрізку АВ відносно α.
335.
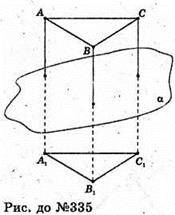
Δ А1 В1С1 симетричний ΔАВС відносно α.
336.
A(a1; а2; a3)
А1 симетрична т. А відносно площини (ху):
A1(a1; а2;
А1 симетрична т. А відносно площини (yz): А2 (a1; а2; a3);
А3 симетрична т. А відносно площини (хz): Α1(a1; а2; a3) .
337.
Відрізки, симетричні відносно деякої площини, належати мимобіжним прямим не можуть, а тим, що перетинаються, можуть.
338.
Можуть, якщо відрізки мають рівні довжини і площина перпендикулярна прямій.
339.
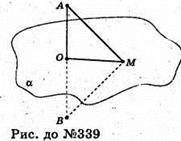
А і В симетричні відносно α. О – точка перетину АВ і α. М? α.
Тоді ΔΑΟΜ = ΔВОМ (AO = ОВ, бо А і В – симетричні за умовою;
ОМ – спільний катет ∠AOM = ∠BOM = 90°). Звідси AM = ВМ.
340.
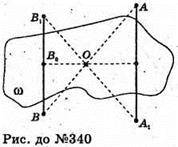
Відрізок А1В1,
341.
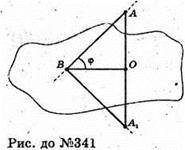
∠ΑΒА1 = 2 × ∠ΑΒΟ – 2φ, але якщо 2φ > 90°, то кутом між прямими
Вважається гострий кут, тобто суміжний з кутом 2φ.
Отже, якщо φ < 45°, то ∠ΑΒΑ1 = 2φ, якщо φ > 45°, то ∠ΑΒΑ, = 180° – 2φ.
342.
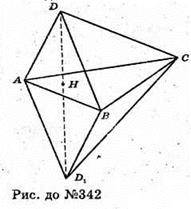
Тетраедр ABCD, симетричний тетраедру ABCD відносно площини (ABC).
343.
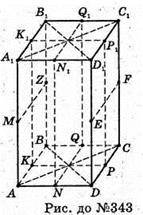
Правильна чотирикутна призма має 5 площин симетрії:
Площини (АА1С1С), (BB1D1D), (ΚΚ1Ρ Ρ), (NN1Q1Q), (MZFE),
Де K1 – середина А1В1,; P1 – середина C1D1; Q1 – середина В1С1;
N1 – середина A1D1; К — середина АВ; Q – середина ВС;
Р – середина CD; N – середина AD; М – середина АА1;
N – середина ВВ1; F – середина СС1; Е – середина DD1.
344.
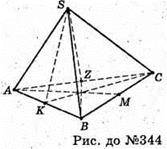
Правильна трикутна піраміда має три площини симетрії:
Це кожна площина, яка проходить через бічне ребро піраміди і
Апофему бічної грані, яка не містить це бічне ребро.
Таких площин три: (SAM); (SBZ); (SCK).
345.
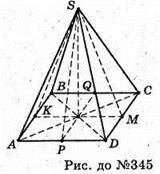
Правильна чотирикутна піраміда має чотири площини симетрії:
(SBD); (SAC); (SKM); (SPQ), де K – середина АВ;
Q – середина ВС; М – середина CD; Р – середина AD.
346.
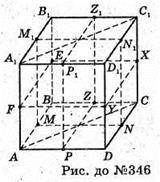
Площини симетрії куба: (AA1C1C); (BB1D1D ); (ΜΜ1Ν1Ν );
(ΡΡ1Ζ1Ζ); (FEXY); (A1B 1CD);(BCD1A); (A1D1CВ); (B1C1DA).
347.
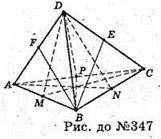
Площини симетрії правильного тетраедра:
ADN (N – середина ВС); BDP (Р – середина АС); CDM (М – середина АВ);
ВСF (F – середина AO); ВАЕ (Е – середина DC); САО (О – середина BD).
348.
Точки А і В знаходяться на однаковій відстані від площини (XZ) і (AB) + (XZ).
Тому А і В симетричні відносно площини (XZ).
349.
А) А(4; 2; -3) і В(-4; 2; -3) симетричні відносно площини (YZ );
Б) М(-3; 2; 6) і В(-3; 2; -6) симетричні відносно площини (XY);
В) Р(7; -2; -4) і K(7; 2; -4) симетричні відносно площини (ΧΖ).
350.
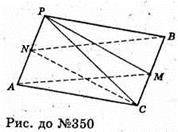
Тетраедр АВСР має дві площини симетрії: (NCB) (Ν – середина АР)
І (АРМ) (М – середина СВ).
351.
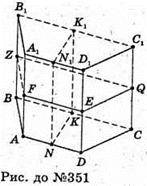
Пряма призма, в основі якої рівнобічна трапеція, має дві площини симетрії:
1) (ΝΝ1Κ1Κ), де N, N1, Κ1, Κ – середини основ трапеції ABCD і A1B1C1D1.
2) (FEQZ), де F, E, Q, Ζ – середини бічних ребер ВВ1; CC1; DD1; АА1.
Якщо в основі призми лежить нерівнобічна трапеція, то призма
Має одну площину симетрії: FEQZ.
352.
Якщо в основі піраміди многокутник із парним числом сторін, то піраміда має n площин симетрії, якщо з непарним числом сторін, то також n площин симетрії, де n – кількість вершин основи піраміди.
353.
А(2; -4; 3); В(-6; 2; 1) і – симетричні відносно деякої площини.
Тоді ця площина пройде через О – середину АВ O(-2; -1; 2),
Площина перпендикулярна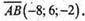
Площина задається рівнянням
-8(x + 2) + 6(у + 1) – 2(z – 2) = 0
-8х -16 + 6y + 6 – 2z + 4 = 0 або
-8х + 6y – 2z – 6 = 0 або
4х – 3у + z + 3 = 0.
354.
А(3; -1; 2); В(1; 2; 4)
Рівняння АВ: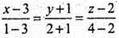 
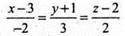
A1 і В1 симетричні А і В відносно площини (ХY) A1(3; -1; -2), В1(1; 2; -4).
Рівняння А1В1: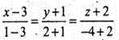 
або 
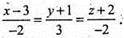
А2 і В2 симетричні А і В відносно площини (YZ) A2(-3; -1; 2), B2 (-1; 2; 4).
Рівняння A2В2: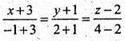 
або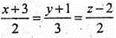 
355.
(х -2)2 + (у -1)2 + (x + 3)2 = 30 – сфера. O(2; 1; -3) – центр сфери.
Площина α проходить через т. А(1; -1; 2), тому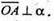 
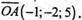
Площина а задається рівнянням:
-1(х – 1) – 2(y + 1) + 5(z – 2) = 0;
-х + 1 – 2у – 2 + 5z – 10 = 0;
-х – 2у + 5z – 11 = 0;
X + 2у – 5z + 11 = 0.
Центр сфери О1, симетричної даній сфері відносно площини,
Має координати (х; у; z), А – середина ОО1.
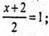х = 0;
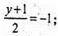y = -3; 
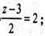z = 7. О1(0;-3;7).
Сфера з центром О1 і радіусом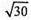 
Задається рівнянням – x2+ (у + 3)2 + (2 – 7)2=30.
356.
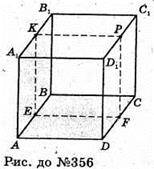
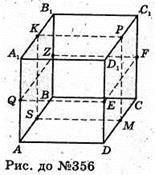
Якщо зафарбовані грані мають спільне ребро, то куб має одну площину симетрії (KPFE), де K, Р, F, Е – середини ребер А1В1; C1D1; CD; AB.
Якщо зафарбовані грані – паралельні, то куб має чотири площини симетрії (A1D1CB); (B1C1DA); (KPMS); (FEQZ).
357.
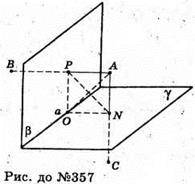
AN + γ; NC = AN.
АР + β; АР = ΡΒ.
AN + γ; проведемо NO + a (NO? PA), тоді АО + а.
Отже, АО – шукана відстань. ΔВАС – прямокутний. ΔPAN – прямокутний.
ΔBАС – ΔPAN. BA : PN = 2 м, тому ВС : PN – 2,
Звідси PΝ = 3м. PANO – прямокутник, тому АО = PN = 3 (м).
358.
Ні, невірно. Можуть бути симетричними, а можуть і не бути симетричними.
360.
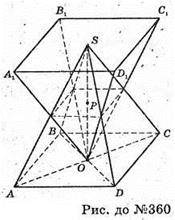
Див. рис.
361.
Нехай т. А1(x1, у1; z1) – точка, симетрична точці А(1; -2; 3) відносно площини
2х – у + 3z + 1 = 0, тоді середина відрізка А1А належить площині
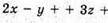
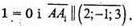
Отже,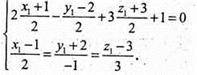 
Із другого рівняння
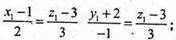
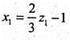
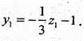
Підставляючи x, і у1 у перше рівняння системи, одержимо:
2х1 + 2 – у1 + 2 + 3z1 +11 = 0 .
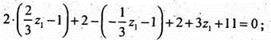
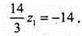
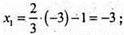
Z1 = -3; тоді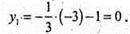 
Отже, А1(-3; 0;-3).
(1 votes, average: 5.00 out of 5)
Loading...