Перпендикулярні прямі
Розділ 4 Раціональні числа і дії мідними
§51. Перпендикулярні прямі
Дві прямі, що мають одну спільну точку, називають прямими, що перетинаються. Їх спільну точку називають точкою перетину.
На малюнку 89 прямі а і b перетинаються, М – точка їх перетину. Дві прямі, перетинаючись, окрім розгорнутих, утворюють чотири кути зі спільною вершиною, градусна міра яких менша від 180°. Прямі АВ і CD (мал. 90) перетинаються в точці O, причому один з утворених кутів – прямий: ∠AOD = 90°. У цьому випадку прямі АВ і CD називають перпендикулярними (від латинського
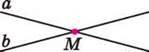
Мал. 89
Оскільки кут COD – розгорнутий (∠COD = 180°), то ∠COA = 180° – ∠AOD = 180° – 90° = 90°. Аналогічно міркуючи, маємо: ∠COB = 90°,∠BOD = 90°.
– Прямі, що перетинаються під прямим кутом, називають перпендикулярними.
Отже, на малюнку 90 прямі АВ і CD – перпендикулярні. Перпендикулярність прямих позначають знаком ⊥. Записують: АВ ⊥ CD, читають: “пряма АВ перпендикулярна до прямої CD”.
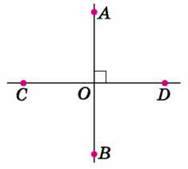
Мал. 90
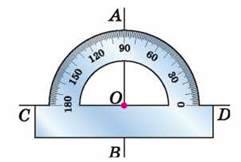
Мал. 91
Для побудови перпендикулярних прямих можна використати транспортир (мал. 91) або креслярський
Приклад. Нехай дано точку M, яка не належить прямій а. Використовуючи креслярський косинець, побудуй пряму, яка проходить через точку М і є перпендикулярною до прямої а.
Розв’язання. 1) Розмістимо косинець так, щоб одна зі сторін його прямого кута лежала на прямій а, а друга проходила через точку М (мал. 92).
2) Проведемо відрізок уздовж сторони косинця від точки М до перетину з прямою а. Позначимо отриману точку буквою N (мал. 92).
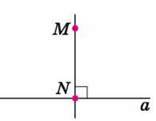
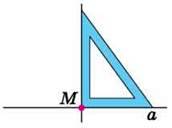
3) Побудуємо пряму MN (мал. 93). Запишемо: MN ⊥ а. Аналогічно можна за допомогою косинця виконати побудову прямої, перпендикулярної до прямої а, якщо точка М належить прямій а (мал. 94).
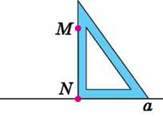
Мал. 92
Мал. 93
Мал. 94
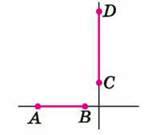
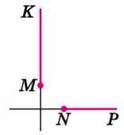
Відрізки (або промені), що лежать на перпендикулярних прямих, називають перпендикулярними відрізками (або променями).
На малюнку 95 зображено перпендикулярні відрізки АВ і CD, а на малюнку 96 – перпендикулярні промені MK і NP.
Мал. 95
Мал. 96
Які прямі називають перпендикулярними? За допомогою яких інструментів можна побудувати перпендикулярні прямі? Які відрізки і які промені називають перпендикулярними?
1463. На малюнку 90: ZAOD = 90°. Як називають прямі АВ і CD?
1464. Визнач на око, які прямі на малюнках 97-100 є перпендикулярними. Перевір це, користуючись косинцем або транспортиром.
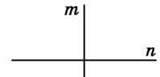
Мал. 97
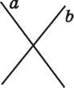
Мал. 98
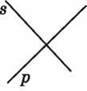
Мал. 99
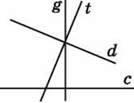
Мал. 100
1465. На малюнку 101 MKPN – прямокутник. Випиши всі пари перпендикулярних прямих.
1466. Наведи з довкілля приклади перпендикулярних прямих.

Мал. 101
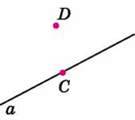
Мал. 102
1467. Накресли пряму а та точки C і D так, як показано на малюнку 102. За допомогою косинця побудуй пряму CK, перпендикулярну до прямої а, та пряму DF, перпендикулярну до прямої а.
1468. Через точку A, що не належить прямій т, побудуй за допомогою косинця пряму n, перпендикулярну до прямої т.
1469. Через точку Q, що належить прямій а, побудуй за допомогою косинця пряму b, перпендикулярну до прямої а.
1470. Знайди всі пари перпендикулярних прямих на малюнку 103. Виконай відповідні записи.
1471. Накресли кут AOB, градусна міра якого дорівнює 65°. На стороні OA познач точку К, віддалену від вершини кута на 3 см. Проведи через точку К прямі, перпендикулярні до прямих АО і ВО.
1472. Накресли кут MKP, градусна міра якого дорівнює 50°. На стороні KP познач точку A, віддалену від вершини кута на 2,5 см. Проведи через точку A прямі, перпендикулярні до прямих KM і KP.
1473. Накресли чотирикутник ABCD такий, що:
1) АВ 1 ВС;
2) АВ 1 ВС, АВ 1 AD;
3) АВ 1 AD, ВС 1 CD.
1474. Накресли гострокутний трикутник АВС. Проведи через кожну його вершину пряму, перпендикулярну до протилежної сторони. Виконай відповідні записи.
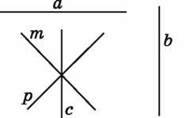
Мал. 103
1475. Накресли тупокутний трикутник MNK. Проведи через кожну з його вершин пряму, перпендикулярну до прямої, що містить протилежну сторону (наприклад, через вершину M проведи пряму, перпендикулярну до прямої, що містить сторону NK). Виконай відповідні записи.
1476. Запиши всі цілі числа, що містяться на координатній прямій між числами: 1) -5,73 і 0,8; 2) -14,9 і -5,7.
1477. Сплав містить дві частини цинку і п’ять частин заліза. Визнач масу сплаву, якщо заліза в ньому на 768 г більше, ніж цинку.
1478. Доведи, що зі ста натуральних чисел від 1 до 100 не можна вибрати сімдесят одне число так, щоб їх сума дорівнювала сумі інших чисел.