Поняття про обернену функцію
УРОК 17
Тема. Поняття про обернену функцію
Мета уроку: формування понять: оборотна функція, обернена функція. Вивчення алгоритму знаходження формули функції, оберненої до даної, властивості графіків взаємно-обернених функцій.
І. Аналіз контрольної роботи
II. Сприймання і усвідомлення нового матеріалу
На уроках математики ви неодноразово розв’язували задачу: обчислити значення функції у = f(x) при заданому значенні х0 аргументу. Іноді потрібно розв’язати і обернену задачу: обчислити значення аргументу х, при якому функція
При розв’язуванні оберненої задачі виникають питання: Скільки таких значень існує? При яких умовах задача має єдиний розв’язок?
Розглянемо приклади.
Приклад 1. Нехай задано функцію у = 2х + 1. Щоб знайти значення аргументу х, при яких функція дорівнює у0, треба розв’язати рівняння у0 = 2х + 1.
Розв’язавши його 2х = у0 – 1;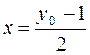 
, маємо, що для будь-якого у0 рівняння у0 = 2х + 1 має і притому тільки один корінь.
Приклад 2. Для функції у = х2 рівняння у0 = х2 при у0 > 0 має два корені: х1 = –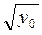
; х2 = .
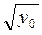Функція,
Залежність із прикладу 1: 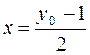виражає х як деяку функцію від у (аргумент цієї функції позначений літерою у, а значення функції – літерою х). Перейшовши до звичних позначень (аргумент – х, функція – у), матимемо функцію: 
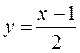, яка називається оберненою до функції у = 2х + 1.
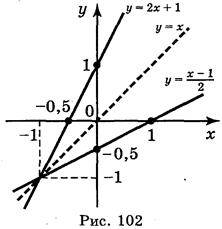
Побудуємо графіки функцій у = 2х + 1 і 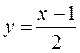в одній системі координат (рис. 102), графіки цих функцій розташовані симетрично відносно бісектриси першого і третього координатних кутів.
Виконання вправи.
З’ясуйте, чи оборотна функція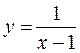 
в області її визначення. Якщо дана функція оборотна, то задайте обернену до неї функцію і побудуйте графіки даної і оберненої функцій.
Розв’язання.
Оскільки функція 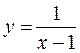набуває кожного свого значення в єдиній точці області визначення (х 
(-
; 1) 
(1; +)), то дана функція оборотна.
Розв’яжемо рівняння 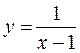відносно х: у(х – 1) = 1, х – 1 = 
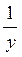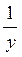, х = + 1.
Замінивши х на у, й у на х маємо у =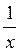 
+1 – обернену функцію х до функції .
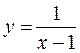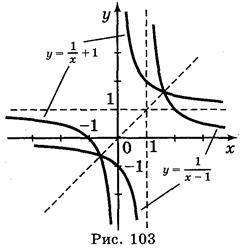
Побудуємо графіки функцій 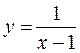та у = 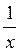+1 в одній системі координат (рис. 103).
Підведемо підсумки:
1) Якщо функція у = f(x) задана формулою, то для знаходження оберненої функції потрібно розв’язати рівняння f(x) = у відносно х, а потім поміняти місцями х і у. Якщо рівняння f(x) = у має більше ніж один корінь, то функції, оберненої до функції у = f(x) не існує.
2) Графіки даної функції і оберненої до даної симетричні відносно прямої у = х.
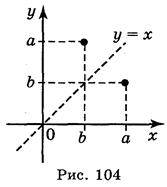
Дійсно, при симетрії відносно прямої у = х вісь абсцис переходить у вісь ординат, а вісь ординат переходить у вісь абсцис, будь-яка точка (а; b) координатної площини при симетрії відносно прямої у = х переходить у точку (b; а) (рис. 104). Якщо точка (а; b) належить графіку даної функції, то точка (b; а) належить графіку оберненої функції, а ці дві точки симетричні відносно прямої у = х.
3) Якщо функція у = f(x) зростає (спадає) на деякому проміжку, то вона оборотна. Обернена функція до даної, визначена області значень функції у = f(x), також є зростаючою (спадною).
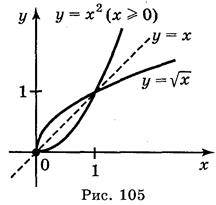
Приклад 3. Функція у = х2 не є оборотною в області визначення. Проте функція у = х2, де х [0; +) зростає на цьому проміжку, тому має обернену. Оберненою функцією є функція у =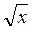 
. Графіки цих функцій зображено на рис. 105.
Виконання вправ____________
1. Які із поданих функцій є оборотними в області визначення:
А) у = 5х + 4; б) у = х3 + 1; в) у = х2 – 1; г)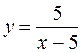 
; д) у = sin х; є) у = 
?
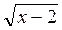Відповідь: а); б); г); є).
2. Знайдіть функцію, обернену до даної:
А) у = х – 3; б) у = 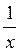; в) у = 
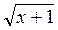; г) у = x2, де х (-; 0].
Відповідь: а) у = х + 3; б) у = 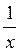; в) у = х2 – 1, де х [0; +); г) у = –.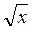
3. На одному і тому же рисунку побудуйте графік даної функції і функції, оберненої до даної:
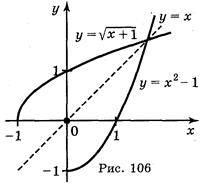
А) у = х2 – 1, х > 0;
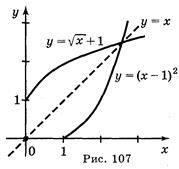
Б) у = (х – 1)2, х > 1;
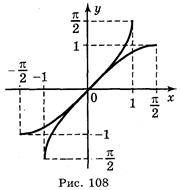
В) у = sin х, х 
;
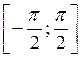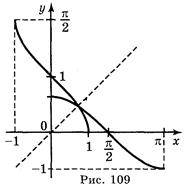
Г) у = cos х, х [0; ?].
Відповідь: а) рис. 106; б) рис. 107; в) рис. 108; г) рис. 109.
4. Скільки коренів має рівняння (розв’язати графічно):
А) х3 + х = 2; б) sin х = 1, х 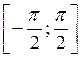; в) sin х = 1?
Відповідь: а) один; б) один; в) безліч.
III. Підсумок уроку
Познайомилися з поняттями оборотної та оберненої функції, властивостями графіків даної функції та оберненої, властивостями монотонності даної функції та оберненої до даної.
IV. Домашнє завдання
Розділ II § 1 (Поняття про обернену функцію). Запитання і завдання для повторення стор. 135 № 1-5.
(1 votes, average: 5.00 out of 5)
Loading...