Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин
Урок 15
Тема. Розміщення двох площин у просторі. Паралельні площини. Ознака паралельності площин
Мета уроку: формування знань учнів про взаємне розміщення двох площин у просторі. Вивчення ознаки паралельності двох площин.
Обладнання: стереометричний набір, схема “Взаємне розміщення двох площин”.
Хід уроку
1. Перевірити наявність виконаних завдань та відповісти на запитання, які виникли в учнів під час їх виконання.
2. Самостійна робота.
Варіант 1
1) Трикутник АВF і трапеція АВСD (AB || CD) лежать у різних площинах.
2) Пряма а паралельна площині a. Доведіть, що в площині a існує пряма, яка мимобіжна прямій а. (8 балів)
1) Трикутник АВК і паралелограм АВСD лежать у різних площинах. Доведіть, що пряма СD паралельна площині АВК. (4 бали)
2) Пряма а паралельна площині a. Доведіть, що в площині a існує пряма, яка паралельна прямій а. (8 балів)
Варіант 3
1) Дано куб АВСDА1B1С1D1. Доведіть, що пряма АС паралельна площині А1С1D. (4 бали)
2) Дано мимобіжні прямі а і b. Доведіть, що існує площина, яка містить пряму а і паралельна прямій b. (8 балів)
1) У трикутній піраміді SАВС точки М. і N
2) Дано паралельні прямі а і b. Доведіть, що існує площина, яка містить пряму а і паралельна прямій b. (8 балів)
Ми знаємо, якщо дві різні площини мають спільну точку, то вони перетинаються по прямій (аксіома С2). Звідси випливає, що дві площини або перетинаються по прямій, або не перетинаються, тобто не мають спільних точок (демонструємо схему, наведену нижче).
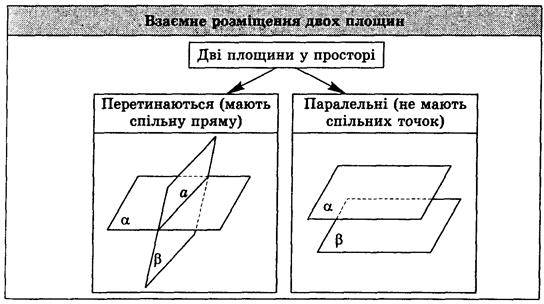
Дві площини називаються паралельними, якщо вони не перетинаються.
Уявлення про паралельні площини дають підлога і стеля кімнати, дві протилежні стіни, поверхня стола і площина підлоги. Якщо площини a і b паралельні, пишуть: a || b.
Виконання вправ
1. Наведіть приклади паралельних площин із оточення.
2. На моделях куба, прямокутного паралелепіпеда покажіть паралельні та площини, що перетинаються.
3. Користуючись зображенням прямокутного паралелепіпеда АВСDА1B1С1D1, укажіть:
А) грані, які перетинають грань АВСD;
Б) площини, які паралельні площині АВС.
4. Площини a і b паралельні. Доведіть, що кожна пряма площини a паралельна площині b.
Ознака паралельності площин
Формулюється ознака паралельності площин і проводиться доведення її згідно з підручником. Доречно зробити записи в зошитах.
Теорема.
Дано:
A1 I a; а2 I a; a1 і a2 перетинаються в точці А; b1 I b ; b2 I b; a1 || b1; а2 || b2 (рис. 59).
Довести: a || b.
Припустимо, що a і b перетинаються по с. Оскільки a1 || b1, то а1 || b, отже, а1 || с. Оскільки а2 || b2 то а2 || b, отже, а2 || с. Через точку А проходять дві прямі а1 і а2, які паралельні с, що суперечить аксіомі паралельності. Отже, a || b.
Виконання вправ
1. Дано куб АВСDА1В1С1D1. Доведіть паралельність площин:
А) АВС і А1В1С1;
Б) АВ1D1 і ВDС1.
2. Точка В лежить поза площиною a. Проведіть через точку В площину, паралельну площині a.
3. Задача № 19 із підручника (с. 19).
4. Доведіть, що площини a і b паралельні, якщо дві прямі а і b, які лежать у площині a і перетинаються, паралельні площині b.
5. Відомо, що дві прямі, які лежать у площині a, паралельні двом прямим площини b. Чи випливає з цього, що a || b?
6. Задача № 20 із підручника (с. 19).
III. Домашнє завдання
§2, п. 10; контрольні запитання № 7, 8; задача № 18 (с. 19).
Запитання до класу
1) Як можуть розташовуватися дві площини у просторі?
2) Сформулюйте ознаку паралельності площин.