Розв’язування ірраціональних нерівностей
УРОК 39
Тема. Розв’язування ірраціональних нерівностей
Мета уроку. Познайомити учнів з узагальненим методом інтервалів. Формування умінь розв’язувати ірраціональні нерівності.
І. Перевірка домашнього завдання
1. Перевірити розв’язування вправ № 71 (3), 67 (1), 79 (1) за розв’язаннями на дошці, заготовленими до уроку.
2. Самостійна робота
Розв’яжіть рівняння: А) Б) В) | Розв’яжіть рівняння: A) Б) В) |
Відповідь: В-1: а) коренів немає; б) 6; в) коренів немає.
В-2: а) 4; б) 5; в) коренів немає.
II. Сприймання і усвідомлення узагальненого методу інтервалів розв’язування нерівностей
Розв’язком нерівності f(x) > 0 (f(x) < 0) можуть бути тільки числа, що входять в область визначення функції у = f(x). Розв’язком нерівності f(x) > 0 є ті інтервали
На рис. 138 і 139 зображено графіки двох функцій. На рис. 138 графік розривається в точках х = – 1 і х = 1 і знак функції змінюється при переході через точки -1 і 1. На рис. 139 знак функції змінюється при переході графіка з нижньої півплощини у верхню (і навпаки), тобто в тих точках, де графік перетинає вісь ОХ. На осі ОХ значення функції дорівнює нулю, тому значення аргументу, при яких функція дорівнює 0, називаються нулями функції.
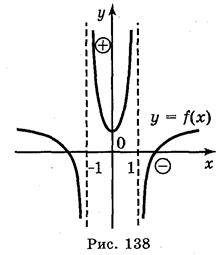
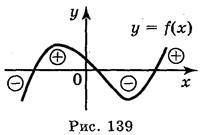
Отже, будь-яка функція може змінювати свій знак тільки в точках, де розривається графік функції, або в нулях.
Отже, щоб розв’язати нерівність f(x) > 0 (f(x) < 0) треба:
1. Знайти область визначення функції у = f(x). (Коли ми знаходимо область визначення функції, то при цьому виділяються і точки, у яких розривається графік функції).
2. Знайти нулі функції (розв’язати рівняння f(x) = 0).
3. На координатній прямій позначити нулі функції на області визначення функції і визначити знак функції на кожному інтервалі, на які розбивають нулі область визначення (у кожному із цих інтервалів функція зберігає знак, і його можна визначити в якій-небудь точці цього інтервалу).
4. Записати відповідь (вибрати інтервали, де функція має потрібний знак).
Розв’язування нерівності таким чином називається розв’язуванням нерівності методом інтервалів. Строге обгрунтування цього методу може бути зроблено в курсі 11 класу.
Розв’яжемо нерівність із вправи 85 (б): 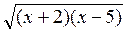 < 8 – х.
< 8 – х.
Розв’язання
Приведемо нерівність до вигляду 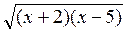 – 8 + х < 0.
– 8 + х < 0.
Введемо функцію у = 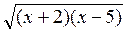 – 8 + х і знайдемо значення х, при яких у < 0. Для цього:
– 8 + х і знайдемо значення х, при яких у < 0. Для цього:
1. Знайдемо область визначення функції: (х+2)(х-5) 0 D(y) = (-
0 D(y) = (- ; -2]
; -2] 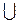 [5; +
[5; + ) (рис. 140).
) (рис. 140).
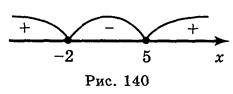
2. Знайдемо нулі функції:
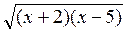 – 8 + х = 0,
– 8 + х = 0, 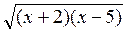 = 8 – х, (х + 2)(х – 5) = 64 – 16х + х2,
= 8 – х, (х + 2)(х – 5) = 64 – 16х + х2,
Х2 – 3х – 10 = 64 – 16х + х2, 13х = 74, х = 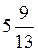 .
.
3. Наносимо нуль функції на область визначення функції (рис. 141):

Знаходимо знак на кожному з трьох інтервалів, на які розбивається область визначення нулем функції:
F(-3) = 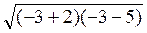 – 8 – 3 =
– 8 – 3 = 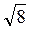 – 8 – 3 < 0,
– 8 – 3 < 0,
F(5,5) = 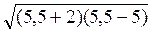 – 8 + 5,5 =
– 8 + 5,5 = 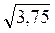 – 2,5 < 0,
– 2,5 < 0,
F(6) = 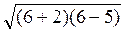 – 8 + 6 =
– 8 + 6 = 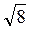 – 2 > 0 і записуємо відповідь.
– 2 > 0 і записуємо відповідь.
Відповідь: (- ; – 2]
; – 2] 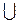
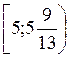 .
.
Розв’язування вправи № 85 (2; 3).
III. Підведення підсумків уроку
IV. Домашнє завдання
Вправа № 85 (1; 3) до розділу III.
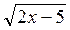 =
= 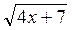 . (4 бали)
. (4 бали)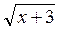 –
– 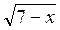 class=""/> = 2. (4 бали)
class=""/> = 2. (4 бали)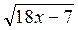 =
= 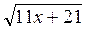 . (4 бали)
. (4 бали)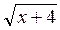 –
– 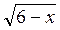 = 2. (4 бали)
= 2. (4 бали)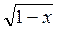 = х – 3. (4 бали)
= х – 3. (4 бали)