Розв’язування найпростіших тригонометричних нерівностей
УРОК 29
Тема. Розв’язування найпростіших тригонометричних нерівностей
Мета уроку: формування умінь учнів розв’язувати найпростіші тригонометричні нерівності: tg t > a, tgt < a, ctg t < a, ctg t > a (tgt  a, tgt
a, tgt 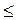 a, ctg t
a, ctg t 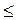 a, ctg t
a, ctg t  a).
a).
І. Перевірка домашнього завдання
1. Відповіді на запитання, які виникли в учнів у процесі виконання домашніх завдань.
2. Фронтальна бесіда з учнями з використанням рис. 130.
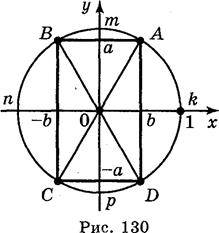
1) Яка дуга відповідає
2) Розв’язком якої нерівності є дуга АmВ; AkD; CpD; СnВ?
3) Розв’яжіть нерівності: cos t  1; sin t > 5; sin t < 5; sin t < -1; cos t >?; cos t <?; cos t
1; sin t > 5; sin t < 5; sin t < -1; cos t >?; cos t <?; cos t  0; cos t
0; cos t 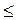 0; sin t
0; sin t  0; sin t
0; sin t 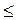 0.
0.
II. Сприймання і усвідомлення розв’язування найпростіших тригонометричних нерівностей
На сьогоднішньому уроці ми продовжимо вчитися розв’язувати найпростіші тригонометричні нерівності.
Розглянемо приклади.
Приклад 1. Розв’яжіть
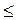 1.
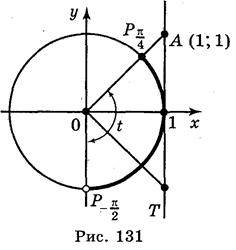
1.Побудуємо одиничне коло та лінію тангенсів (рис. 131). На осі тангенсів позначимо число 1. Якщо t є розв’язком нерівності, то ордината точки Т, рівна tg t, повинна бути не більша 1. Множина таких точок Т – промінь AT. Множина точок 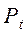 , що відповідають точкам променя АТ, – дуга
, що відповідають точкам променя АТ, – дуга 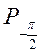
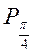 , яка на рисунку виділена. (Зверніть увагу: точка
, яка на рисунку виділена. (Зверніть увагу: точка 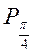 належить, а точка
належить, а точка 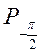 не належить множині розв’язків). Отже, розв’язком нерівності будуть усі значення t із проміжку
не належить множині розв’язків). Отже, розв’язком нерівності будуть усі значення t із проміжку 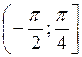 . Враховуючи, що період функції tg t дорівнює?, маємо розв’язок даної нерівності
. Враховуючи, що період функції tg t дорівнює?, маємо розв’язок даної нерівності 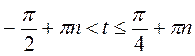 , n
, n Z.
Z.
Відповідь: 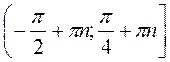 , де n
, де n Z.
Z.
Приклад 2. Розв’яжіть нерівність tg t > 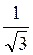 .
.
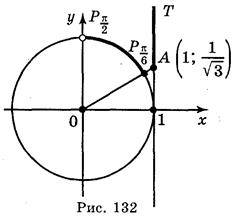
На осі тангенсів (рис. 132) позначимо число 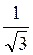 і множину значень тангенсів, не менших за
і множину значень тангенсів, не менших за 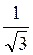 (промінь AT). На одиничному колі множина точок, що відповідають кутам, тангенс яких не менший від
(промінь AT). На одиничному колі множина точок, що відповідають кутам, тангенс яких не менший від 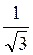 , є дуга
, є дуга 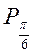
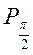 . Отже, розв’язком нерівності будуть усі значення t із проміжку
. Отже, розв’язком нерівності будуть усі значення t із проміжку 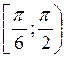 . Враховуючи періодичність, маємо:
. Враховуючи періодичність, маємо: 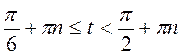 , де n
, де n Z.
Z.
Відповідь: 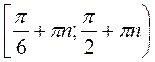 , де n
, де n Z.
Z.
Приклад 3. Розв’яжіть нерівність ctgt  –
–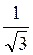 .
.
1 спосіб. Враховуючи, що ctg t = tg 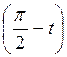 , маємо ctg t = – tg
, маємо ctg t = – tg 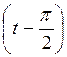 , тоді маємо нерівність – tg
, тоді маємо нерівність – tg 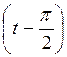
 –
– 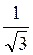 a6o tg
a6o tg 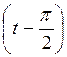
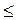
 . Розв’яжемо останню нерівність (рис. 133), маємо:
. Розв’яжемо останню нерівність (рис. 133), маємо: 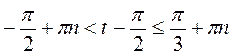 , n
, n Z;
Z; 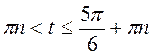 , n
, n Z.
Z.
Відповідь: 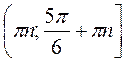 , де n
, де n Z.
Z.
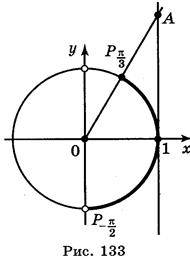
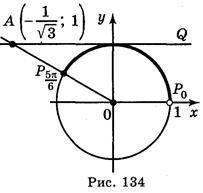
2 спосіб. На осі котангенсів позначимо число і множину (рис. 134) значень котангенсів, не менших за –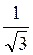 (промінь AQ). На одиничному колі множина точок, що відповідають кутам, котангенс яких не менший від –
(промінь AQ). На одиничному колі множина точок, що відповідають кутам, котангенс яких не менший від –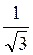 , є дуга
, є дуга 
 Отже, розв’язки нерівності будуть усі значення t із проміжку
Отже, розв’язки нерівності будуть усі значення t із проміжку 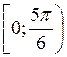 . Враховуючи періодичність, маємо:
. Враховуючи періодичність, маємо: 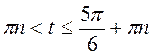 , n
, n Z.
Z.
Відповідь: 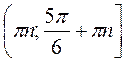 , де n
, де n Z.
Z.
III. Формування умінь розв’язувати найпростіші нерівності
1. Розв’яжіть нерівності: a) tg x  – 1; б) tg x <
– 1; б) tg x < 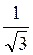 ; в) tg х
; в) tg х  2; г) ctg х >
2; г) ctg х >  .
.
Відповідь: а) 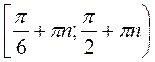 , n
, n Z; б)
Z; б) 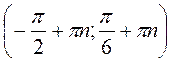 , n
, n Z; в)
Z; в) 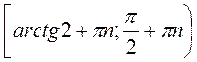 , n
, n Z; г)
Z; г) 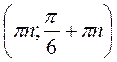 , n
, n Z.
Z.
IV. Підведення підсумків уроку
V. Домашнє завдання
Розділ II § 5. Запитання і завдання для повторення до розділу II № 24. Вправа № 3 (2, 4, 6, 8).