Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Тематичне оцінювання № 2

Тематичне оцінювання № 2

Урок 24

Тема. Тематичне оцінювання № 2

Мета уроку: перевірка навчальних досягнень учнів з теми “Паралельність прямих і площин у просторі”.

Хід уроку

Тематичне оцінювання № 2 можна провести шляхом проведення тематичної контрольної роботи.

1. Тематична контрольна робота № 2

Варіант А

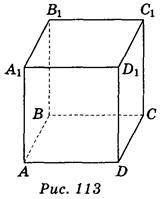
1. Користуючись зображенням куба ABCDA1В1C1D1 (рис. 113), запишіть ребра куба, які паралельні грані ABCD. (3 бали)

2. Сторона АВ трикутника АВС лежить у площині?, а вершина С не лежить в цій площині. Точки М і N –

середини сторін АС і ВС відповідно. Доведіть, що пряма MN паралельна площині?. (3 бали)

3. Дано дві паралельні площини? і?. Точки А і В належать площині?, точки С і D – площині?. Відрізки AD і ВС перетинаються в точці М, АВ = 10 см, BM = 6 см, CM = 12 см. Знайти довжину відрізка CD. (3 бали)

4. Побудуйте переріз куба ABCDA1B1C1D1 площиною, яка проходить через точки А, В і D1. (3 бали)

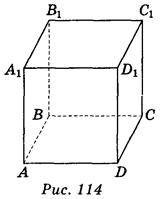
1. Користуючись зображенням куба ABCDA1B1C1D1 (рис. 114), запишіть грані куба, які паралельні ребру AA1. (3 бали)

2. Дві сторони даного трикутника паралельні площині?. Доведіть, що і третя його сторона паралельна цій площині. (3 бали)

Площина? перетинає сторони АВ і ВС трикутника АВС в точках М і N відповідно і паралельна стороні АС. Знайти довжину відрізка MN, якщо АС = 24 см, а ВМ:АМ = 3:1. (3 бали)

4. Побудуйте переріз куба ABCDA1B1C1D1 площиною, яка проходить через діагональ ВС1 грані куба і паралельна діагоналі АС грані куба. (3 бали)

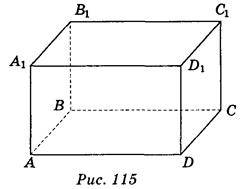
1. Користуючись зображенням прямокутного паралелепіпеда ABCDA1B1C1D1 (рис. 115), укажіть ребра, які паралельні площині BDD1. (3 бали)

2. Основа AD трапеції ABCD лежить у площині?, а точки В і С не належать цій площині. Доведіть, що пряма ВС паралельна площині?. (3 бали)

3. Дано дві паралельні площини? і?. Промінь SC перетинає площину? в точці А, а площину? – в точці С; промінь SD перетинає площину? в точці В, а площину? – в точці D; SA = 14 см, SC = 42 см, CD = 18 см. Знайти довжину відрізка АВ. (3 бали)

4. Побудуйте переріз куба ABCDA1B1C1D1 площиною, яка проходить через точки В, С і A1. (3 бали)

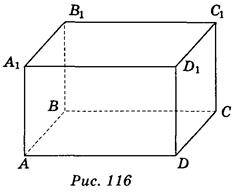
1. Користуючись зображенням прямокутного паралелепіпеда (рис. 116), запишіть грані прямокутного паралелепіпеда, які паралельні прямій ВС. (3 бали)

2. Сторони даного гострого кута паралельні площині?. Доведіть, що і бісектриса цього кута паралельна цій площині. (3 бали)

3. Площина? перетинає сторони АВ і ВС трикутника АВС в точках М і N відповідно і паралельна стороні АС. Знайти сторону АС трикутника, якщо АС – MN = 8 см, ВМ : МА = 2:1. (3 бали)

4. Побудуйте переріз куба ABCDA1B1C1D1 площиною, яка проходить через діагональ AD1 грані куба і паралельна діагоналі BD грані куба. (3 бали)

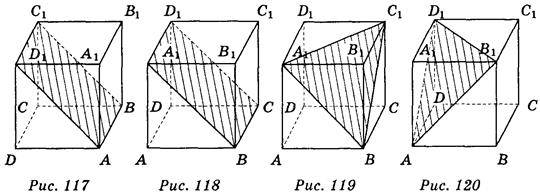
Відповідь. Варіант 1. 1. А1В1, В1С1, C1D1, А1D1. 3. 20 cm. 4. (Рис. 117)

Варіант 2. 1. ВСС1В1, DCC1D1. 3. 18 cm. 4. (Рис. 118)

Варіант 3. 1. АА1, СС1. 3. 6 cm. 4. (Рис. 119)

Варіант 4. 1. ADD1A1, A1B1C1D1. 3. 24см. 4. (Рис. 120)

Варіант Б

1. Дано трикутну піраміду SABC. Точки К, L, М – середини ребер SA, SB, SC відповідно.

А) Яке взаємне розміщення прямої KL та площини АВС? (2 бали)

Б) Яке взаємне розміщення площин KLM та АВС? (2 бали)

В) Яке взаємне розміщення площин АВС та KLS? (2 бали)

2. Чи правильне твердження: якщо дві прямі, які лежать в одній площині, паралельні двом прямим другої площини, то ці площини паралельні? Відповідь обгрунтуйте. (3 бали)

3. У прямокутному паралелепіпеді ABCDA1B1C1D1 точка Н належить ребру CD. Побудуйте переріз паралелепіпеда площиною, яка проходить через цю точку і паралельна площині перерізу ACD1. (3 бали)

1. Дано прямокутний паралелепіпед АВСDА1В1С1D1.

А) Яке взаємне розміщення прямої А1В1 та площини АВС? (2 бали)

Б) Яке взаємне розміщення площин ACD1 та А1С1В? (2 бали)

В) Яке взаємне розміщення площин ACD1 та BB1D1? (2 бали)

2. Чи правильне твердження: якщо дві прямі, які лежать в одній площині, паралельні другій площині, то ці площини паралельні? Відповідь обгрунтуйте. (3 бали)

3. У трикутній піраміді SABC точки Е, К, Р належать ребрам АВ, SB, SC відповідно, причому РК ВС. Побудуйте переріз тетраедра площиною ЕКР. (3 бали)

1. Дано трикутну піраміду SABC. Точки К, L, М – середини ребер SA, SB, SC відповідно.

А) Яке взаємне розміщення прямої АВ та площини КLМ? (2 бали)

Б) Яке взаємне розміщення площин KLM та АВС? (2 бали)

В) Яке взаємне розміщення площин KLC та АВМ? (2 бали)

2. Яким може бути взаємне розташування прямих а і b, якщо пряма а лежить в площині?, а пряма b паралельна цій площині? Відповідь обгрунтуйте. (3 бали)

3. У прямокутному паралелепіпеді ABCDA1B1C1D1 точки К, Р, М належать відповідно ребрам АА1, A1B1 і ВС. Побудуйте переріз паралелепіпеда площиною КРМ. (3 бали)

1. Дано куб ABCDA1B1C1D1. Точки К, L, М – середини ребер АВ, AD, АА1 відповідно.

А) Яке взаємне розміщення прямої KL та площини BDC1? (2 бали)

Б) Яке взаємне розміщення площин KLM та BDA1? (2 бали)

В) Яке взаємне розміщення площин KLM та BDC1? (2 бали)

2. Яким може бути взаємне розташування двох прямих, якщо обидві вони паралельні одній площині? Відповідь обгрунтуйте. (3 бали)

3. У тетраедрі SABC точка Е належить ребру АС. Побудуйте переріз тетраедра площиною, яка проходить через точку Е і паралельна ребрам AD і ВС. Визначте вигляд перерізу. (3 бали)

Тематичне оцінювання № 2 можна провести за допомогою тесту, тексти якого подано нижче.

При оцінюванні виконання тестів враховуються тільки ті шість із виконаних завдань, яким відповідає найбільша кількість балів.

Мета даного тесту – перевірити, чи вміє учень:

– зображати та знаходити на малюнках прямі, що перетинають площину і паралельні їй;

– розв’язувати задачі, використовуючи ознаку паралельності прямої і площини;

– зображати та знаходити на малюнках паралельні площини і площини, що перетинаються;

– розв’язувати задачі на взаємне розміщення площин, використовуючи відповідні властивості та ознаки.

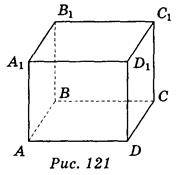
1. Дано зображення прямокутного паралелепіпеда (рис. 121). Яка з вказаних площин паралельна прямій СD? (1 бал)

A) AA1D; б) ABB1; в) ВВ1D1; г) AD1C.

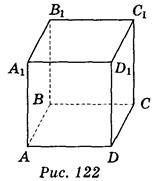
2. Дано зображення куба ABCDA1B1C1D1 (рис. 122). Яка з вказаних площин паралельна площині BDA1? (1 бал)

А) В1D1А; б) АСВ1; в) А1С1D1; г) В1D1С.

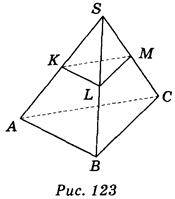
3. Точки К, L, М – середини ребер SA, SB, SC тетраедра SABC (рис. 123). Яке взаємне розміщення площин АВС і KLM? (1 бал)

А) Перетинаються; б) збігаються; в) паралельні; г) визначити неможливо.

II рівень

1. Відрізок АВ не перетинає площину?, С – середина відрізка АВ. Через точки А, В, С проведені паралельні прямі, які перетинають площину а відповідно в точках А1, В1, С1. (рис. 124). Знайдіть АА1, якщо ВВ1 = 4 cm; CC1 = 3 см. (1 бал)

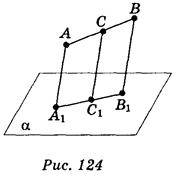
А) 1 см; б) 2 см; в) 3 см; г) 4 см.

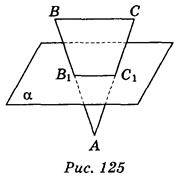
2. Площина? перетинає сторони АВ і AC трикутника АВС відповідно в точках В1 і С1, ВС || ? (рис. 125). Знайдіть ВС, якщо В1С1 = 1 см, ВВ1 : В1А = 3:1. (1 бал)

А) 1 см; б) 2 см; в) 3 см; г) 4 см.

3. Дано площину? і точку А поза нею. Скільки існує різних прямих, які проходять через точку А і паралельні?? (1 бал)

А) Одна; б) жодної; в) дві; г) безліч.

1. Точки К, L, М, N є серединами відповідно ребер SA, ВА, ВС, SC тетраедра SABC. Знайдіть периметр чотирикутника KLMN, якщо АС = m, SB = n. (2 бали)

А) 2m; 6) 2n; в) m + n; г) .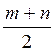

2. У просторі дано дві паралельні прямі а і b, а також точку А, що не належить їм. Скільки існує площин, які проходять через точку А і паралельні прямим а і b? (2 бали)

А) Одна; б) жодної; в) дві; г) безліч.

3. Які з вказаних фігур можуть бути паралельною проекцією трапеції? (2 бали)

А) Квадрат; б) трапеція; в) ромб; г) трикутник.

IV рівень

1. АВСDА1В1С1D1 – куб, К – середина ребра СС1. Визначити число сторін перерізу куба площиною, яка проходить через точки В, К, А. (3 бали)

А) 3; б) 4; в) 5; г) 6.

2. Яку фігуру утворюють усі відрізки, що сполучають будь-які точки двох мимобіжних відрізків? (3 бали)

А) Чотирикутник; б) площину; в) тетраедр; г) відрізок.

3. ABCD – квадрат зі стороною 6 см. Точка S віддалена від кожної вершини квадрата на 7 см. Знайдіть відстані від середини відрізка SA до середин сторін квадрата. (3 бали)

А) 2,5 см; б) 3,5 см; в) 4,5 см; г) 5,5 см.

І рівень

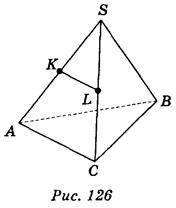
1. Дано зображення тетраедра SABC (рис. 126). Точки К, L – середини ребер SA і SB. Яка з вказаних площин паралельна прямій KL? (1 бал)

A) SAC; б) SAB; в) SBC; г) АВС.

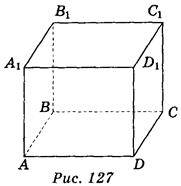
2. Дано зображення прямокутного паралелепіпеда ABCDA1B1C1D1 (рис. 127). Яка із вказаних площин паралельна площині АВС? (1 бал)

A) BDC1; б) А1В1С1; в) BCD; г) DCC1.

3. Дано зображення куба ABCDA1B1C1D1 (рис. 128). Яке взаємне розміщення площин АСВ1 і A1C1D? (1 бал)

А) Перетинаються; б) збігаються; в) паралельні; г) визначити неможливо.

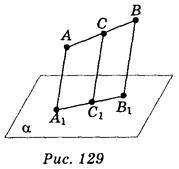
1. Відрізок АВ не перетинає площину?, С – середина відрізка АВ. Через точки А, В, С проведено паралельні прямі, які перетинають площину а відповідно в точках А1, В1, С1 (рис. 129). Знайдіть СС1, якщо АА1 = 2 см; ВВ1 = 4 см. (1 бал)

А) 4 см; б) 3 см; в) 2 см; г) 1 см.

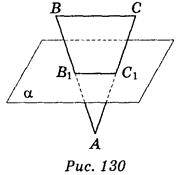
2. Площина? перетинає сторони АВ і АС трикутника АВС відповідно в точках В1 і С1, ВС || ? (рис. 130). Знайдіть АС, якщо АС1 = 2 см, ВС:В1С1=2:1. (1 бал)

А) 1 см; б) 2 см; в) 3 см; г) 4 см.

3. Дано площину? і точку А поза нею. Скільки існує площин, що проходять через точку А і паралельні?? (1 бал)

А) Одна; б) жодної; в) дві; r) безліч.

1. Точки К, L, М, N є серединами відповідно ребер SA, АС, ВС, BS тетраедра SABC. Знайдіть периметр чотирикутника KLMN, якщо кожне ребро тетраедра дорівнює а. (2 бали)

А) а; б) 2а; в) 3а; г) 4а.

2. У просторі дано дві мимобіжні прямі а і b і точку А, що не належить їм. Скільки існує площин, які проходять через точку А і паралельні прямим а і b? (2 бали)

А) Одна; б) жодної; в) дві; г) безліч.

3. Які з вказаних фігур можуть бути паралельною проекцією прямокутника? (2 бали)

А) Квадрат; б) трапеція; в) ромб; г) трикутник.

1. ABCDA1B1C1D1 – куб, К – середина ребра СС1. Визначити число сторін перерізу куба площиною, яка проходить через точки А, В1, К. (3 бали)

А) 3; б) 4; в) 5; r) 6.

2. Прямі а і b – мимобіжні. Знайдіть геометричне місце точок, утворене прямими, кожна з яких перетинає пряму b і паралельна прямій а. (3 бали)

А) Пряма; б) площина; в) тетраедр; г) відрізок.

3. Три паралельні площини перетинають дві мимобіжні прямі в точках А1, А2, А3 і В1, В2, В3. Відомо, що А1А2 = 4 см, В2В3 = 9 см, А2А3 = В1В2. Знайдіть довжину відрізка А1А3. (3 бали)

А) 5 см; б) 10 см; в) 13 см; г) 15 см.

Рівень	Номер завдання	Варіант 1	Варіант 2
1	Б	Г
2	Г	Б
3	В	В
ІІ	1	Б	Б
2	Г	Г
3	Г	А
ІІІ	1	В	Б
2	А, б	А
3	Б	А, в
IV	1	Б	Б
2	В	Б
3	Б, г	Б