Тематичне оцінювання № 3
Урок 34
Тема. Тематичне оцінювання № 3
Мета уроку: перевірка навчальних досягнень учнів з тем “Перпендикулярність прямих”, “Перпендикулярність прямої і площини”.
Хід уроку
Тематичне оцінювання № 3 можна провести у вигляді тематичної контрольної роботи.
1. Тематична контрольна робота № 3
Варіант А
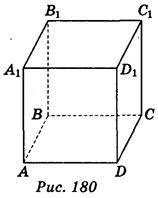
1. Користуючись зображенням куба ABCDA1B1C1D1 (рис. 180), запишіть ребра куба, які перпендикулярні до ребра АА1 і перетинають його. (3 бали)
2. Відстань від точки М до всіх вершин квадрата
3. З точки А, взятої поза площиною?, проведені до неї дві похилі, довжини яких дорівнюють 10 і 17 см. Різниця проекцій цих похилих на площину? дорівнює 9 см. Знайти проекції похилих. (3 бали)
4. Правильний трикутник розташований над площиною. Доведіть, що відстань від центра трикутника до даної площини дорівнює середньому арифметичному відстаней від вершин цього трикутника до цієї площини. (3 бали)
Варіант 2
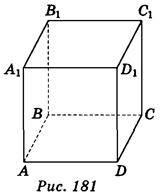
1. Користуючись зображенням куба ABCDA1B1С1D1 (рис. 181), запишіть ребра, які перпендикулярні до грані ABCD.
2. Відстані від точки М до всіх вершин квадрата дорівнюють по 13 см, а до площини квадрата – 12 см. Знайдіть діагональ квадрата. (3 бали).
3. З точки А, взятої поза площиною?, проведено до неї дві похилі. Знайдіть довжини похилої, якщо одна з них на 13 см більша другої, а проекції похилих на площину? дорівнюють 6 і 20 см. (3 бали)
4. Паралелограм розташований над площиною. Доведіть, що сума відстаней від протилежних вершин паралелограма до даної площини однакова. (3 бали)
Варіант 3
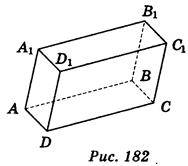
1. Користуючись зображенням прямокутного паралелепіпеда ABCDA1B1C1D1 (рис. 182), запишіть грані, які перпендикулярні до ребра АА1. (3 бали)
2. Відстані від точки S до всіх вершин правильного трикутника дорівнюють по 5 см, а до площини трикутника – 3 см. Знайдіть висоту трикутника. (3 бали)
3. Із деякої точки проведено до даної площини дві похилі. Знайти довжини похилих, якщо проекції похилих дорівнюють 2 і 14 см, а похилі відносяться як 1 : 2. (3 бали)
4. Квадрат розташований над площиною. Доведіть, що відстань від центра квадрата до площини в чотири рази менша суми відстаней від вершин квадрата до площини. (3 бали)
Варіант 4
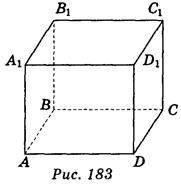
1. Користуючись зображенням прямокутного паралелепіпеда ABCDA1В1C1D1 (рис. 183), запишіть ребра, які перпендикулярні до ребра DC і перетинають його. (3 бали)
2. Відстань від точки М до кожної вершини правильного трикутника дорівнює 10 см. Знайти відстань від точки М до площини трикутника, якщо медіана трикутника дорівнює 9 см. (3 бали)
3. Із деякої точки простору проведено дві похилі, проекції яких дорівнюють 8 і 20 см. Знайти довжини похилих, якщо відомо, що їх різниця дорівнює 8 см. (3 бали)
4. Через вершину D паралелограма ABCD проведено площину, яка не перетинає його. Доведіть, що відстань від точки В до площини дорівнює сумі відстаней від точок А і С до даної площини. (3 бали)
Відповідь. Варіант 1. 1. А1В1, A1D1, AB, AD. 2. 8 см. 3. 6 см і 15 см.
Варіант 2. 1. АА1, ВВ1, СС1, DD1 2. 10 см. 3. 7,5 см і 20,5.см. Варіант 3. 1. ABCD, A1B1D1. 2. 6 см. 3. 8 см і 16 см. Варіант 4. 1. DD1, DA, BC, CC1. 2. 8см. 3. 25 см і 17см.
Варіант Б
Варіант 1
1. Через центр О правильного трикутника АВС проведено перпендикуляр SO до площини АВС.
А) Яка величина кута SOA? (2 бали)
Б) Доведіть, що SA = SB. (2 бали)
В) Знайдіть відстань від точки S до площини АВС, якщо SC = 5 см, 0В = 3 см. (2 бали)
2. Сторона квадрата ABCD дорівнює 8 см. Точка S знаходиться на відстані 16 см від його вершин. Знайдіть відстань від точки S до площини квадрата. (3 бали)
3. У прямокутному паралелепіпеді АВСDА1В1С1D1 АВ1 = 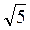 См, АС1 =
См, АС1 = 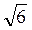 См, АВ = 2 см. Знайдіть відстань між прямою A1D1 та площиною АВ1С1. (3 бали)
См, АВ = 2 см. Знайдіть відстань між прямою A1D1 та площиною АВ1С1. (3 бали)
Варіант 2
1. Через центр О квадрата ABCD проведено перпендикуляр SO до площини АВС.
А) Яка величина кута SOD? (2 бали)
Б) Доведіть, що  SAO =
SAO =  SCO. (2 бали)
SCO. (2 бали)
В) Знайдіть відстань SC, якщо відстань від точки S до площини АВС дорівнює 5 см, a OD = 12 см. (2 бали)
2. Точка S знаходиться на відстані 6 см від вершин прямокутника і на відстані 4 см від його площини. Знайдіть сторони прямокутника, якщо одна з них вдвічі більша за другу. (3 бали)
3. Три відрізки SA, SB, SC мають однакову довжину а,  ASB=
ASB=  BSC =
BSC =  CSA = 60°. Знайдіть відстань від точки S до площини АВС. (3 бали)
CSA = 60°. Знайдіть відстань від точки S до площини АВС. (3 бали)
Варіант 3
1. Через центр О правильного шестикутника ABCDEF проведено перпендикуляр SO до площини АВС.
А) Чому дорівнює кут між прямими SO і AD? (2 бали)
Б) Доведіть, що  ASO =
ASO =  FSO. (2 бали)
FSO. (2 бали)
В) Знайдіть сторону шестикутника, якщо відстань від точки S до площини АВС дорівнює 4 см, а SC = 5 см. (2 бали)
2. Сторона правильного трикутника АВС дорівнює 12 см. Точка S знаходиться на однаковій відстані від його вершин і віддалена від площини трикутника на відстань 4 см. Знайдіть відстань від точки S до вершин трикутника АВС. (3 бали)
3. Ребро куба ABCDA1B1C1D1 дорівнює а. Знайдіть відстань від точки А, до площини AB1D1. (3 бали)
Варіант 4
1. Через точку О перетину діагоналей АС і BD прямокутника ABCD проведено перпендикуляр SO до площини АВС.
А) Чому дорівнює кут між прямими SO і АС? (2 бали)
Б) Доведіть, що SA = SC. (2 бали)
В) Знайдіть відстань від точки S до площини АВС, якщо SC = 10 см, OD = 6 см. (2 бали)
2. Точка S знаходиться на відстані 10 см від вершин рівнобедреного трикутника АВС (АВ = ВС) і на відстані 6 см від його площини. Знайдіть сторони трикутника, якщо  ВАС = 30°. (3 бали)
ВАС = 30°. (3 бали)
3. Три відрізки SA, SB, SC попарно перпендикулярні, SA = SB = SC = а. Знайдіть відстань від точки S до площини АВС. (3 бали)
Тематичне оцінювання № 3 можна провести за допомогою тесту, текст якого подано нижче.
При оцінюванні виконання тестів враховуються тільки ті шість із виконаних завдань, яким відповідає найбільша кількість балів.
Тест
Мета даного тесту – перевірити, чи вміє учень:
– зображати та знаходити на малюнку перпендикулярні прямі та площини;
– розв’язувати задачі, використовуючи ознаку перпендикулярності прямої і площини.
Варіант 1
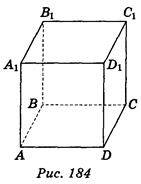
1. Дано зображення куба АВСDА1В1С1D1 (рис. 184). Укажіть пряму, яка перпендикулярна до прямої АА, і проходить через точку С. (1 бал)
А) АВ; б) AC; в) AD; г) АС.
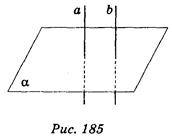
2. Відомо, що різні прямі а і b перпендикулярні до площини? (рис. 185). Як розміщені прямі а і b? (1 бал)
А) Перетинаються; б) мимобіжні; в) паралельні; г) перпендикулярні.
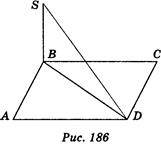
3. Відрізок SB перпендикулярний до площини прямокутника ABCD (рис. 186). Знайдіть відстань між точками S і D, якщо SB = 4 cm, BD = 3 cm. (1 бал)
А) 3 см; б) 4 см; в) 5 cm; r) 7 cm.
II рівень
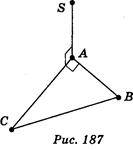
1. Точка S лежить поза площиною трикутника АВС, причому  SAC = 90°,
SAC = 90°,  CAB = 90° (рис. 187). Які з вказаних тверджень правильні? (1 бал)
CAB = 90° (рис. 187). Які з вказаних тверджень правильні? (1 бал)
А) Пряма SA перпендикулярна до площини АВС;
Б) пряма АВ перпендикулярна до площини SAC;
В) пряма АС перпендикулярна до площини SAB;
Г) пряма ВС перпендикулярна до площини ASC.
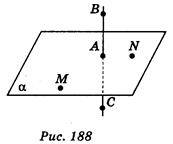
2. Точки А, В, С лежать на прямій, перпендикулярній до площини а, а точки А, М, N лежать у площині а (рис. 188). Які з вказаних кутів прямі? (1 бал)
A)  MAB; б)
MAB; б)  MCA; в)
MCA; в)  CAN ; г)
CAN ; г)  NBA.
NBA.
3. У просторі дано пряму а і точку А поза нею. Скільки існує прямих, перпендикулярних до прямої а і які проходять через точку А? (1 бал)
А) Жодної; б) безліч; в) одна; г) визначити неможливо.
III рівень
1. Прямі АВ і CD перпендикулярні до деякої площини і перетинають її в точках В і D відповідно. Знайдіть АС, якщо АВ = 9 см, CD = 15 см, BD = 8 см і відрізок AC не перетинає даної площини. (2 бали)
А) 8 см; б) 9 см; в) 10 см; г) 15 см.
2. Через вершину В квадрата ABCD проведено пряму BS, перпендикулярну до його площини. Які з наведених тверджень правильні? (2 бали)
А) Пряма SD перпендикулярна до площини АВС;
Б) пряма AD перпендикулярна до площини ASB;
В) пряма CD перпендикулярна до площини BSC;
Г) пряма BD перпендикулярна до площини SBC.
3. Через точку О перетину діагоналей прямокутника ABCD проведено перпендикуляр МО. Знайдіть МО, якщо АВ = 6 см, ВС = 8 см, МА = 13 см. (2 бали)
А) 10 см; б) 11 см; в) 12 см; г) визначити неможливо.
IV рівень
1. Дано паралелограм ABCD і площину?, яка його не перетинає. Через вершини паралелограма проведено прямі, перпендикулярні до площини і які перетинають площину відповідно в точках А1, В1, С1, D1. Знайдіть довжину відрізка DD1, якщо АА1 = 3 см, ВВ1 = 4 см, СС1 =5 см. (3 бали)
А) 2 см; б) 3 см; в) 4 см; г) 5 см.
2. Прямі АВ, АС і AD попарно перпендикулярні. Знайти площу трикутника BCD, якщо АВ = 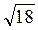 См, АС =
См, АС = 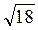 См, AD =
См, AD = 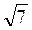 См. (3 бали)
См. (3 бали)
А) 25 см2; б) 16 см2; в) 15 см2; г) 12 см2.
3. Побудовано переріз куба ABCDA1В1C1D1 площиною, що проходить через точки В1 і D1 і середину ребра CD. Знайдіть периметр перерізу, якщо ребро куба дорівнює а. (3 бали)
A) 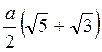 ; б)
; б) 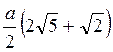 ; в)
; в) 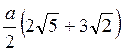 ; г)
; г) 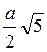 .
.
І рівень
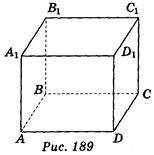
1. Дано зображення прямокутного паралелепіпеда АВСDА1В1С1D1 (рис. 189). Укажіть площину, яка перпендикулярна до прямої AA1 і проходить через точку А. (1 бал)
A) DCC1; б) А1B1С1; в) BCD; г) ВСС1.
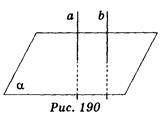
2. Як розташовані площина? і пряма b, якщо a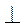 ?, а || b (рис. 190)? (1 бал)
?, а || b (рис. 190)? (1 бал)
А) Не перетинаються;
Б) паралельні;
В) перпендикулярні;
Г) визначити неможливо.
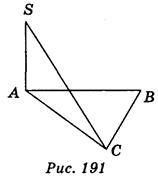
3. Відрізок SA перпендикулярний до площини трикутника АВС (рис. 191). Знайдіть відстань від точки А до точки С, якщо SA = 3 см, SC = 5 см. (1 бал)
А) 3 см; б) 4 см; в) 5 см; г) 6 см.
II рівень
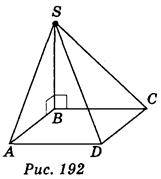
1. Точка S лежить поза площиною ромба ABCD, причому SB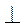 BC, SB
BC, SB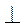 AS.
AS.  BAD = 30° (рис. 192). Які з вказаних тверджень правильні? (1 бал)
BAD = 30° (рис. 192). Які з вказаних тверджень правильні? (1 бал)
А) Пряма SB перпендикулярна до площини ADC;
Б) пряма АВ перпендикулярна до площини SBC;
В) пряма BC перпендикулярна до площини ABS;
Г) пряма SB перпендикулярна до прямої BD.
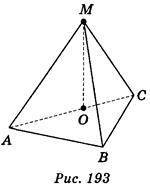
2.  ABC=90°, точка М лежить поза площиною АВС, МА = MB = МС. З точки М проведено відрізок ОМ, який перпендикулярний до площини АВС, точка О лежить у площині АВС (рис. 193). Які з вказаних тверджень правильні? (1 бал)
ABC=90°, точка М лежить поза площиною АВС, МА = MB = МС. З точки М проведено відрізок ОМ, який перпендикулярний до площини АВС, точка О лежить у площині АВС (рис. 193). Які з вказаних тверджень правильні? (1 бал)
А) Точка О лежить усередині трикутника АВС;
Б) точка О лежить поза трикутником АВС;
В) точка О лежить на відрізку АС, причому АО не дорівнює ОС;
Г) точка О лежить на гіпотенузі АС, причому АО дорівнює ОС.
3. У просторі дано пряму а і точку А на ній. Скільки існує прямих, перпендикулярних до прямої а, які проходять через точку А? (1 бал)
А) Жодної; б) безліч; в) тільки одна; г) визначити неможливо.
III рівень
1. Прямі АВ і CD перпендикулярні до деякої площини і перетинають її в точках відповідно. Знайдіть BD, якщо АВ = 6 см, CD = 9 см, AC = 5 см і відрізок АС не перетинає даної площини. (2 бали)
А) 1 см; б) 2 см; в) 3 см; г) 4 см.
2. Через точку О перетину діагоналей прямокутника ABCD проведено перпендикуляр МО до площини АВС. Які з наведених тверджень правильні? (2 бали)
А) Пряма МО перпендикулярна до прямої АС;
Б) пряма МО перпендикулярна до площини BCD;
В) пряма AC перпендикулярна до площини МАВ;
Г) пряма АС обов’язково перпендикулярна до площини MBD.
3. Через вершину В квадрата ABCD проведено пряму BS, перпендикулярну до його площини. Знайдіть відстань від точки S до вершини А квадрата ABCD, якщо АС = 2 cm, SB = 1 cm. (2 бали)
А)  см; б) 1 см; в)
см; б) 1 см; в) 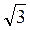 см; г) 2 cm.
см; г) 2 cm.
IV рівень
1. Точка О – точка перетину медіан трикутника АВС, ? – площина, яка не перетинає трикутник АВС. Через точки А, В, С, О проведено прямі, перпендикулярні до площини?, які перетинають площину відповідно в точках А1, В1, С1, О1. Знайдіть довжину відрізка OO1, якщо АА1 = 1 см, ВВ1 = 2 см, СС1 = 3 см. (3 бали)
А) 1 см; б) 2 см; в) 3 см; г) 1,5 см.
2. Дано прямокутний паралелепіпед ABCDA1B1C1D1, в якому BD = 13 см, DC = 5 см, СС1 = 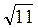 см. Знайдіть площу трикутника ADC1. (3 бали)
см. Знайдіть площу трикутника ADC1. (3 бали)
А) 25 см2; б) 36 см2; в) 72 см2; г) 18 см2,
3. У кубі ABCDA1B1C1D1 побудовано переріз площиною, що проходить через точки А, С, К, де К – середина ребра C1D1. Знайдіть периметр перерізу, якщо ребро куба дорівнює а. (3 бали)
А) 2а; б) 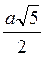 ; в)
; в) 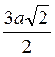 ; г)
; г) 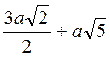 .
.
Відповіді до тестових завдань
Варіант 1 | Варіант 2 | ||
1 | Б | В | |
2 | В | В | |
3 | В | Б | |
ІІ | 1 | В | А, г |
2 | А, в | Г | |
3 | В | Б | |
1 | В | Г | |
2 | Б, в | А, б | |
3 | В | В | |
1 | В | Б | |
2 | Г | Б | |
3 | В | Г |
Якщо в класі виконувалася тематична контрольна робота № 3, то вдома можна запропонувати виконати тест, і навпаки.
У ході фронтальної бесіди з’ясувати, які завдання викликали труднощі, та відповісти на запитання учнів.