Головна ⇒ 📌Довідник з геометрії ⇒ Вектори в просторі – Декартові координати та вектори в просторі
Вектори в просторі – Декартові координати та вектори в просторі
Геометрія
Декартові координати та вектори в просторі
Вектори в просторі
Усі основні означення векторів у просторі залишаються такими самими, як означення векторів на площині (див. розділ “Геометрія. 8 клас”).
Координатами вектора 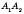 , де
, де 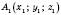 ,
, 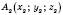 , називають числа
, називають числа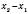 ,
, 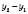 ,
, 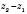 .
.
Вектори рівні тоді, й тільки тоді, коли вони мають відповідно рівні координати. Це дає підставу
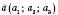 , або просто
, або просто 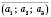 .
.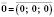 .
.Дії над векторами в просторі позначають так само, як і на площині:
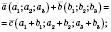
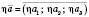 .
.Діють і геометричні правила: правило трикутника, правило паралелограма, правило многокутника.
Так само доводиться, що
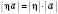 , а напрям вектора
, а напрям вектора 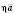 збігається з напрямом
збігається з напрямом 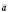 , якщо
, якщо 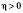 , і протилежний напряму
, і протилежний напряму 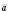 , якщо
, якщо 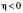
Зберігається поняття колінеарних векторів і його необхідна й достатня умова.
Скалярним добутком векторів
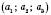 і
і 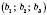 називається число
називається число 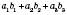 .
.Має місце теорема, за якою скалярний добуток векторів дорівнює добутку їх абсолютних величин і косинуса кута між векторами:
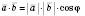 .
.Для того щоб два вектори були перпендикулярними, необхідно й достатньо, щоб їх скалярний добуток дорівнював нулю.
Кожний вектор у просторі можна єдиним способом розкласти за трьома координатними векторами
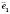 ,
, 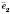 і
і 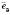 (див. рисунок).
(див. рисунок).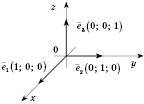
Related posts:
- Вектори у просторі – ВЕКТОРИ Формули й таблиці МАТЕМАТИКА ВЕКТОРИ Вектори у просторі Вектор – спрямований відрізок А – початок вектора В – кінець вектора Модуль вектора – довжина відрізка, який зображує вектор: ||. Два вектори рівні, якщо вони однаково спрямовані і мають рівні модулі. Координати вектора з початком у точці А(x1,y1,z1) і кінцем у точці В(х2,у2,z2). Рівні вектори мають […]...
- Перетворення в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Перетворення в просторі Поняття перетворення для фігур у просторі означають так само, як і на площині (див. розділ “Геометрія. 8 клас”). Рухом Називається перетворення, при якому зберігаються відстані між точками. Властивості руху в просторі: Прямі переходять у прямі, півпрямі – у півпрямі, відрізки – у відрізки, кути між […]...
- Подібність просторових фігур – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Подібність просторових фігур Перетворення фігури F називається Перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюють себе в одну й ту саму кількість разів. Як і на площині, перетворення подібності в просторі переводить прямі у прямі, півпрямі у півпрямі, відрізки у відрізки і зберігає кути між півпрямими. […]...
- Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Урок 58 Тема. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Мета уроку: формування знань учнів про вектори в просторі, дії над векторами, заданими координатами, Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі”. Хід уроку І. Перевірка домашнього […]...
- Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок). Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz. Прямі Ox, Oy, Oz називаються Координатними […]...
- Скалярний добуток векторів Геометрія Вектори Скалярний добуток векторів Скалярним добутком векторів і називається число . Позначення: . . Очевидно, що . Розподільна властивість скалярного добутку: . Кутом між ненульовими векторами і називається кут BAC. Кутом між будь-якими двома ненульовими векторами і називається кут між векторами, що дорівнюють даним і мають спільний початок. Вважають, що кут між однаково напрямленими […]...
- Кут між векторами. Скалярний добуток векторів Урок 59 Тема. Кут між векторами. Скалярний добуток векторів Мета уроку: формування понять кута між векторами, скалярного добутку векторів. Формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі” Хід уроку 1. Фронтальна бесіда з класом за контрольними запитаннями № 18- 20 з використанням схеми “Вектори в просторі” (див. с. 233). […]...
- Координати вектора УРОК № 43 Тема. Координати вектора Мета уроку: формування поняття координат вектора та вміння застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують координати вектора; застосовують вивчені означення і властивості до розв’язування задач. Хід уроку I. […]...
- Координати векторa Геометрія Вектори Координати векторa Нехай вектор має початком точку , а кінцем – точку . Координатами вектора називаються числа і . Позначення: або . . Очевидно, що . Теорема. Вектори рівні тоді й тільки тоді, коли вони мають рівні відповідні координати....
- Координати вектора. Дії над векторами, що задані координатами 1. Запишемо координати вектора: 1) 2) 3) 4) 2. 1) 2) 3) 4) 5) 6) 3. 1) Запишемо розклад за координатними векторами: 2) Запишемо розклад за координатними векторами: 3) Запишемо розклад за координатними векторами: 4) Знайдемо координати векторів : Знайдемо координати вектора Запишемо розклад за координатними векторами: 5) Знайдемо координати векторів Знайдемо координати вектора Запишемо […]...
- Скалярний добуток векторів УРОК № 49 Тема. Скалярний добуток векторів Мета уроку: формування поняття скалярного добутку векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: формулюють означення скалярного добутку, його властивості; застосовують вивчені означення та властивості до розв’язування […]...
- Колінеарні вектори УРОК № 48 Тема. Колінеарні вектори Мета уроку: формування поняття “колінеарні вектори”; вивчення властивості та ознаки колінеарних векторів; формування вмінь учнів застосовувати вивчені означення та властивості до розв’язування завдань. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують колінеарність векторів; застосовують вивчені означення та […]...
- Декартові координати у просторі – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Декартові координати у просторі М – точка у просторі М(х, у, x) Мхy – проекція точки М на площину хоу; Мхy(х, о, у) Мх, Му, Mz – проекції точки М на осі OX, OY, OZ відповідно. Мх(х, о, о); Му(о, у, о); Мz(о, о, z). Відстань між точками А(x1,y1,z1) і […]...
- Додавання векторів Геометрія Вектори Додавання векторів Сумою векторів і називається вектор . Додавання векторів має переставну та сполучну властивості: ; для будь-яких , , . Теорема. Які б не були точки A, B, C, справджується векторна рівність: . Правило трикутника додавання векторів Щоб знайти суму довільних векторів і , треба від кінця вектора (див. рисунок) відкласти вектор […]...
- Множення вектора на число Геометрія Вектори Множення вектора на число Добутком вектораНа число називається вектор , тобто . Для будь-якого вектора і чисел і . Для будь-яких двох векторів і і числа . Теорема 1. Абсолютна величина вектора дорівнює . Напрям вектора , якщо , збігається з напрямом вектора , якщо , і протилежний напряму вектора , якщо . […]...
- Розв’язування задач на застосування векторів Урок 60 Тема. Розв’язування задач на застосування векторів Мета уроку: формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: стінна таблиця “Вектори в просторі”. Хід уроку І. Перевірка домашнього завдання 1. Два учні відтворюють розв’язування задач № 55 (4), 56. 2. Фронтальне опитування. 1) Чому дорівнює скалярний добуток векторів, які задано координатами? 2) Як […]...
- Розкладання вектора за координатними осями Геометрія Вектори Розкладання вектора за координатними осями Вектор називається Одиничним, якщо його абсолютна величина дорівнює одиниці. Одиничні вектори, які мають напрями додатних координатних півосей, називаються Координатними векторами, або Ортами (див. рисунок). Позначення: ; . Оскільки координатні вектори відмінні від нуля й неколінеарні, то будь-який вектор можна розкласти за цими векторами: ....
- Координати і вектори у просторі 776. А(2; 0; 0), В(0; 0; 3), С(0; 5; -4), D(4; -3; 0), Е(2; 6; 4), F(6; -2; -6). 777. А(2; 0; 5), В(-4; 0; 2), С(4; 0; -2), D(1; 3; 1), A? хОz, В? xОz, C? xOz. Основа тетраедра ABC лежить у координатній площині хОz, Тому що yА = yB = yC = 0. […]...
- Розв’язування задач координатно-векторним методом 1. 1) Введемо прямокутну систему координат із початком у точці В і спрямуємо вісь Оx вздовж ребра BA, Oz – вздовж ВВ1. Довжину ребра куба позначимо як а. Тоді координати точок: А(а; 0; 0;); С(0; а; 0); R(а; а; 0); C1(0; а; а). Знайдемо координати векторів і Знайдемо довжини векторів: Знайдемо кут між векторами: Кут […]...
- Додавання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри Векторні величини (вектори) – це величини, які характеризуються числовими значеннями і напрямом: Скалярні величини (скаляри) – це величини, які характеризуються лише числовим значенням. Вони можуть бути додатними та від’ємними й додаються алгебраїчно. 3.1. Додавання векторів Якщо вектори спрямовані вздовж однієї прямої або якщо вони паралельні, то результуючий вектор дорівнює алгебраїчній сумі […]...
- Векторний добуток векторів 1. Векторний добуток векторів є вектором, а скалярний – числом. Векторний та скалярний добуток мають однакові властивості (крім комутативності). 2. За означенням модуля векторного добутку А отже, оскільки то 3. 1) За означенням У нашому випадку Скористаємось основною тригонометричною тотожністю: Тоді 2) За означенням У нашому випадку Скористаємось основою тригонометричною тотожністю: Тоді Оскільки 3) Рівність […]...
- Вектори у просторі 156. ABCDEF – правильний шестикутник. А) Б) В) Але 157. 158. А) Б) В) 159. 160. А) Б) В) 161. 162. А(х; у; z). Тому -5 – х = З, x = -8; 4 – у = 4, у = 0; 1 – z = 2, z = -1. Отже, А(-8; 0; -1). 163. С(-2; […]...
- Додавання векторів УРОК № 44 Тема. Додавання векторів Мета уроку: формування вміння додавати вектори, вивчення властивостей суми векторів; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують додавання векторів; відкладають вектор, що дорівнює сумі векторів; формулюють […]...
- ОПЕРАЦІЇ З ВЕКТОРНИМИ ВЕЛИЧИНАМИ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 1. ОСНОВИ КІНЕМАТИКИ 1.2. ОПЕРАЦІЇ З ВЕКТОРНИМИ ВЕЛИЧИНАМИ Вектор – напрямлений відрізок. Векторні величини мають числове значення (модуль), напрям, точку прикладання (рис. 3). Рис. З Проекція вектора на вісь Ох – довжина відрізка, який сполучає проекцію початку вектора на вісь Ох з проекцією кінця вектора на ту саму […]...
- Множення вектора на число УРОК № 47 Тема. Множення вектора на число Мета уроку: формування вміння множити вектор на число; вивчення властивостей множення вектора на число; формування вмінь застосовувати вивчені значення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують множення вектора на число; […]...
- Віднімання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри 3.3. Віднімання векторів Різницею двох векторів, спрямованих по одній прямій або паралельних один одному, є алгебраїчна різниця цих векторів. Щоб знайти різницю двох векторів, які мають різні напрями, треба розмістити обидва вектори так, щоб вони виходили з однієї точки. Потім сполучити кінці векторів вектором, спрямованим від від’ємника до зменшуваного. Цей вектор […]...
- Віднімання векторів УРОК № 45 Тема. Віднімання векторів Мета уроку: формування вмінь віднімати вектори, вивчення властивостей різниці векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують віднімання векторів; відкладають вектор, що дорівнює різниці векторів; формулюють властивості […]...
- Вектори і координати 74. 1) 2) B i C, A i D; 3 ) 4 ) 75. 76. I – паралелограм. 77. – паралелограм 80. 1) 2) 3) 81. 1) 2 ) 3) 4) 82. 1) φ = 60°. 2) φ = 180°, cos 180° = -1. 3) φ = 42°. 4) φ = 17°12′. 83. α ≈ […]...
- Вектор. Модуль і напрям вектора. Рівність векторів УРОК № 42 Тема. Вектор. Модуль і напрям вектора. Рівність векторів Мета уроку: формування понять вектора, модуля вектора, напряму вектора; рівності векторів; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують вектор, модуль і […]...
- Координати – Кінематика 5. Механіка 5.1. Кінематика 5.1.5. Координати Координати точки – це числа, які визначають положення фізичного тіла (матеріальної точки) на площині чи в просторі. В декартовій системі координат положення тіла (матеріальної точки) на лінії площини і в просторі визначається відповідно однією (а), двома (б) або трьома (в) координатами (X, Y, Z)....
ГАЛЬЯ »