Головна ⇒ 📌Довідник з математики ⇒ Розв’язування найпростіших тригонометричних нерівностей
Розв’язування найпростіших тригонометричних нерівностей
Математика – Алгебра
Тригонометричні функції
Розв’язування найпростіших тригонометричних нерівностей
Найзручнішим є спосіб розв’язування тригонометричних нерівностей за допомогою тригонометричного кола.
Приклади
1) 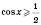 . Побудуємо одиничне коло (див. рисунок нижче). Проведемо пряму
. Побудуємо одиничне коло (див. рисунок нижче). Проведемо пряму 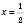 . Вона перетинає коло у двох точках. Одна з них відповідає куту
. Вона перетинає коло у двох точках. Одна з них відповідає куту 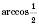 або
або 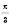 , друга – куту
, друга – куту 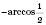 або
або 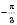
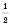 , другої дуги – меншу.
, другої дуги – меншу.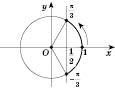
Щоб описати всі точки потрібної дуги, “пройдемо” по ній у додатному напрямку, тобто проти годинникової стрілки. Ураховуючи періодичність функції
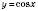 , дістанемо відповідь:
, дістанемо відповідь: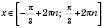 , n Є Z.
, n Є Z.2)
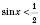 . Діючи аналогічно, отримаємо рисунок, на якому зображена пряма
. Діючи аналогічно, отримаємо рисунок, на якому зображена пряма 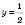 :
: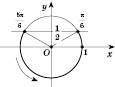
Умову задачі задовольняють
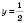 .
.Але щоб записати проміжок, треба точку
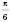 записати в другому вигляді. Для цього додамо
записати в другому вигляді. Для цього додамо  до
до 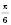 :
: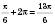 .
.Ураховуючи період, дістанемо відповідь:
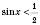 при
при 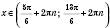 ,
, n Є Z.
3)
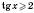 . Ураховуючи, що функція
. Ураховуючи, що функція 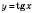 є зростаючою на кожному з проміжків виду
є зростаючою на кожному з проміжків виду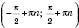 , n Є Z,
, n Є Z,отримуємо
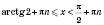 , n Є Z.
, n Є Z.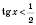 ,
, 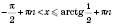 , n Є Z.
, n Є Z.



 (1 votes, average: 5.00 out of 5)
(1 votes, average: 5.00 out of 5)Related posts:
- Розв’язування найпростіших тригонометричних нерівностей УРОК 29 Тема. Розв’язування найпростіших тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати найпростіші тригонометричні нерівності: tg t > a, tgt < a, ctg t < a, ctg t > a (tgt a, tgt a, ctg t a, ctg t a). І. Перевірка домашнього завдання 1. Відповіді на запитання, які виникли в учнів у процесі […]...
- Розв’язування найпростіших тригонометричних рівнянь Математика – Алгебра Тригонометричні функції Розв’язування найпростіших тригонометричних рівнянь 1. cos x = a Розв’язки рівняння шукатимемо, спираючись на рисунок 1 або на рисунок 2. Якщо , розв’язків немає. , , . , , . , , . Рис. 2 Загальний випадок : , x = ±arccosa + 2πn,. У випадках, коли , , теж […]...
- Розв’язування тригонометричних нерівностей УРОК 30 Тема. Розв’язування тригонометричних нерівностей Мета уроку: формування умінь учнів розв’язувати тригонометричні нерівності. І. Перевірка домашнього завдання. 1. Відповіді на запитання, які виникли у учнів при виконанні домашнього завдання. 2. Фронтальна бесіда з учнями з використанням рис. 135. 1) Які дуги відповідають нерівностям: Tg t > a, tg t < a, tg t > […]...
- Розв’язування тригонометричних рівнянь, систем та нерівностей УРОК 31 Тема. Розв’язування тригонометричних рівнянь, систем та нерівностей Мета уроку. Систематизувати навички і уміння розв’язувати тригонометричні рівняння, нерівності, системи. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування нерівностей із домашнього завдання. 2. Колективне розв’язування нерівностей: A) sin 2x sin x – cos 2x cos х . Sin 2x sin x – cos 2x […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = a УРОК 21 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння sin t = а Мета уроку: засвоєння учнями виведення і застосування формули для коренів рівняння sin t = а. Обладнання: Таблиця “Рівняння sin t = а”. І. Перевірка домашнього завдання 1. Відповіді на питання, що виникли при виконанні домашніх завдань. 2. Самостійна робота. Варіант 1 Розв’яжіть рівняння: […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg t = a УРОК 22 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння tg T = a. Мета уроку: зсвоєння учнями виведення і застосування формули для знаходження коренів рівняння tg t = a (ctg t = а). Обладнання: Таблиця “Рівняння tg t = а і ctg t = a”. І. Перевірка домашнього завдання 1. Перевірити наявність домашніх завдань в зошитах […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos t = a УРОК 20 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos T = a Мета уроку: засвоєння учнями виведення і застосування формули для знаходження коренів рівняння cos t = a. Обладнання: Таблиця “Рівняння cos t = a”. І. Перевірка домашнього завдання Математичний диктант Обчисліть: 1) arcsin ; 2) arcos ; 3) arctg ; 4) arcsin; 5) arccos; […]...
- Розв’язування нерівностей з однією змінною Математика – Алгебра Нерівності Розв’язування нерівностей з однією змінною Розв’язком нерівності з однією змінною називається значення цієї змінної, яке перетворює її на правильну числову нерівність. Розв’язати нерівність означає знайти всі її розв’язки або довести, що їх немає. Дві нерівності називають Рівносильними, якщо вони мають одні й ті самі розв’язки або не мають розв’язків. Числові проміжки […]...
- Системи нерівностей з однією змінною Математика – Алгебра Нерівності Системи нерівностей з однією змінною Розв’язком системи нерівностей з однією змінною називають значення змінної, яке є розв’язком кожної нерівності даної системи. Розв’язати систему нерівностей означає знайти всі її розв’язки або показати, що їх немає. Щоб розв’язати систему нерівностей, кожну її нерівність поступово спрощують, замінюючи рівносильною. Розглянемо на простих прикладах, як застосувати […]...
- Деякі способи розв’язування тригонометричних рівнянь Математика – Алгебра Тригонометричні функції Деякі способи розв’язування тригонометричних рівнянь 1. Рівняння, що зводяться до квадратних . легко виразити через за допомогою основної тригонометричної тотожності : . Отже, ; . Нехай , . ; ; . 1) ; , k Є Z. 2) ; , k Є Z. Відповідь: , k Є Z; , k […]...
- Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання значення виразу УРОК № 6 Тема. Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання значення виразу Мета уроку: закріплення учнями змісту: властивостей числових нерівностей і теорем про почленне додавання та множення нерівностей; наслідків із властивостей числових нерівностей. Відпрацювання навичок: відтворювати зміст вивчених понять; застосовувати їх для розв’язування вправ: на порівняння виразів, на доведення нерівностей, […]...
- Розв’язування ірраціональних нерівностей УРОК 39 Тема. Розв’язування ірраціональних нерівностей Мета уроку. Познайомити учнів з узагальненим методом інтервалів. Формування умінь розв’язувати ірраціональні нерівності. І. Перевірка домашнього завдання 1. Перевірити розв’язування вправ № 71 (3), 67 (1), 79 (1) за розв’язаннями на дошці, заготовленими до уроку. 2. Самостійна робота Розв’яжіть рівняння: А) = . (4 бали) Б) – = 2. […]...
- Розв’язування нерівностей, що містять показникову функцію УРОК 49 Тема. Розв’язування нерівностей, що містять показникову функцію Мета уроку. Познайомити учнів зі способами розв’язування показникових нерівностей. І. Перевірка домашнього завдання Відповіді на запитання, що виникли в учнів під час виконання домашніх завдань. II. Аналіз самостійної роботи, проведеної на попередньому уроці ІІІ. Сприймання і усвідомлення розв’язування найпростіших показникових нерівностей та тих, що безпосередньо зводяться […]...
- Властивості числових нерівностей Математика – Алгебра Нерівності Властивості числових нерівностей a, b, с, d – довільні числа. 1. Якщо і , то . 2. Якщо до обох частин правильної нерівності додати одне й те саме число, то дістанемо правильну нерівність. 3. Якщо обидві частини правильної нерівності помножити на одне й те саме додатне число, то дістанемо правильну нерівність. […]...
- Розв’язування логарифмічних нерівностей УРОК 61 Тема. Розв’язування логарифмічних нерівностей Мета уроку. Формування умінь учнів розв’язувати логарифмічні нерівності І. Перевірка домашнього завдання Перевірити наявність виконаних домашніх завдань та відповісти на запитання, що виникли в учнів при виконанні цих завдань. II. Сприймання і усвідомлення розв’язування логарифмічних нерівностей (які розв’язуються введенням нової змінної) Приклад 1. Розв’яжіть нерівність log х – log5 […]...
- Розв’язування показникових рівнянь, систем і нерівностей УРОК 51 Тема. Розв’язування показникових рівнянь, систем і нерівностей Мета уроку. Формування умінь розв’язувати показникові рівняння, системи і нерівності. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування вправи № 2 (11; 13; 16). 2. Колективне розв’язування нерівностей, аналогічних домашнім: вправи № 2 (30; 31). II. Аналіз самостійної роботи, проведеної на попередньому уроці III. Формування […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- Циліндр, вписаний у кулю Геометрія Комбінації геометричних тіл Циліндр, вписаний у кулю Основи циліндра є рівновіддаленими від центра кулі (рисунок нижче зліва). Ця комбінація тіл є симетричною відносно будь-якої площини, що проходить через центр кулі паралельно твірним циліндра. У перерізі тіла такою площиною дістанемо прямокутник і описане навколо нього коло (рисунок справа). Прямокутник ABCD є осьовим перерізом циліндра, а […]...
- Конус, вписаний у кулю Геометрія Комбінації геометричних тіл Конус, вписаний у кулю Вершина конуса лежить на сфері (рисунок нижче зліва). Основа конуса лежить на сфері. Комбінація є симетричною відносно площини, що містить вісь конуса. У такому перерізі дістанемо трикутник, вписаний у коло (рисунок справа). Трикутник рівнобедрений. Бічні сторони – твірні конуса, коло – велике коло описаної кулі. Отже, радіус […]...
- Побудова графіків тригонометричних функцій УРОК 9 Тема. Побудова графіків тригонометричних функцій Мета уроку: побудова графіків функцій у = sin х, у = cos x, у = tg х, у = ctg x. Формування умінь будувати графіки функцій: у = Asin (kx + b), у = Acos (kx + b), у = Atg (kx + b), у = Actg (kx […]...
- Зображення нерівностей земної поверхні на плані та карті Географія Загальна географія Земля на плані та карті Зображення нерівностей земної поверхні на плані та карті Усі нерівності земної поверхні називають Рельєфом. Щоб зобразити його на плані чи карті, необхідно виміряти висоту окремих ділянок земної поверхні. Для цього використовують нівелір. За його допомогою визначають, на скільки метрів вершина горба вища за його підошву. Цей процес […]...
- Графіки тригонометричних функцій Математика – Алгебра Тригонометричні функції Графіки тригонометричних функцій Для побудування графіків тригонометричних функцій візьмемо . Побудуємо графік функції (див. рисунок). Ця крива називається синусоїдою. Графік функції можна дістати з графіка функції паралельним перенесенням його вліво вздовж осі Ox на одиниць. Це випливає з формули . Побудуємо графік функції : Зверніть увагу: значення , , не […]...
- Квадратна нерівність. Розв’язування квадратних нерівностей УРОК № 25 Тема. Квадратна нерівність. Розв’язування квадратних нерівностей Мета уроку: закріпити знання учнів про зміст означення квадратних нерівностей та схему їх розв’язування; удосконалити вміння учнів розв’язувати квадратні нерівності та нерівності, що зводяться до квадратних шляхом рівносильних перетворень, а також виробити вміння використовувати ці вміння під час розв’язування систем квадратних нерівностей та для розв’язування задач […]...
- Властивості тригонометричних функцій УРОК 10 Тема. Властивості тригонометричних функцій Мета уроку: вивчення властивостей тригонометричних функцій у = sin х, у = cos х, у = tg х, у = ctg x (область визначення; область значень; парність (непарність); симетричність графіків; періодичність; нулі; проміжки спадання (зростання); проміжки знакопостійності; найбільші і найменші значення). І. Перевірка домашнього завдання Перевірити правильність побудови графіків […]...
- Розв’язування показникових нерівностей УРОК 50 Тема. Розв’язування показникових нерівностей Мета уроку. Формування умінь учнів розв’язувати показникові нерівності. І. Перевірка домашнього завдання 1. Відповіді на запитання, що виникли в учнів при виконанні домашніх завдань. 2. Усне розв’язування показникових нерівностей з використанням таблиці 21 для усних обчислень “Показникові нерівності “. 1 2 3 4 5 1 2х > 8 2х […]...
- Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною УРОК № 14 Тема. Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною Мета уроку: закріплення учнями знань змісту понять: нерівність з однією змінною, розв’язок нерівності з однією змінною та що означає розв’язати нерівність з однією змінною; система нерівностей з однією змінною, розв’язок системи нерівностей з однією змінною та що означає розв’язати систему нерівностей з […]...
- Приклади розв’язування системи тригонометричних рівнянь Математика – Алгебра Тригонометричні функції Приклади розв’язування системи тригонометричних рівнянь 1) Відповідь: , n Є Z; , n Є Z. 2) а) б) Відповідь: , n, k Є Z; , n, k Є Z....
- Періодичність тригонометричних функцій Математика – Алгебра Тригонометричні функції Періодичність тригонометричних функцій Функція називається Періодичною з періодом , якщо для будь-якого x з області визначення функції числа і також належать області визначення й виконується умова: . Якщо T – період функції , то всі числа виду nT, де , , також є періодами функції. Щоб побудувати графік періодичної функції […]...
- Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Формування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...
- Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах2+bx+c. Розв’язування квадратних нерівностей” УРОК № 26 Тема. Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах 2 + b х + С. Розв’язування квадратних нерівностей” Мета уроку: повторити, систематизувати й узагальнити знання та вміння учнів щодо змісту вивчених у розділі “Функція та її властивості” понять і схем розв’язування типових задач шляхом складання загальних алгоритмів розв’язування задач. […]...
- Основні властивості числових нерівностей УРОК № 4 Тема. Основні властивості числових нерівностей Мета уроку: домогтися засвоєння учнями змісту поняття “оцінити значення виразу”; закріпити знання учнів про зміст властивостей числових нерівностей та їхніх наслідків. Продовжити роботу з вироблення вмінь: відтворювати зміст вивчених властивостей, наслідків із них і їх доведення; застосовувати властивості числових нерівностей та наслідки з них для розв’язування вправ […]...
- РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ТАБЛИЦЕЮ. СКЛАДАННЯ НЕРІВНОСТЕЙ Мета: формувати навички розв’язування задач на спосіб зведення до одиниці, складання нерівностей; удосконалювати знання таблиць множення і ділення, вміння використовувати їх на практиці; розвивати обчислювальні навички, логічне мислення, пізнавальну активність, творчі здібності; виховувати уважність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання – Прочитайте вираз до задачі 255. 35 : […]...
- Приклади розв’язування типових задач з геометрії для найпростіших фігур Геометрія Приклади розв’язування типових задач з геометрії для найпростіших фігур Треба добре розуміти: коли ми доводимо теорему або розв’язуємо задачу, кожне твердження треба обгрунтувати, тобто показати, що воно випливає з якої-небудь аксіоми чи раніше доведеної теореми. Якщо ви спираєтеся на якусь теорему, ретельно перевірте, чи повністю виконано її умову. Наприклад, при застосуванні першої ознаки рівності […]...
- Періодичність тригонометричних функцій УРОК 8 Тема. Періодичність тригонометричних функцій Мета уроку: Введення поняття періодичної функції; знаходження найменших додатних періодів тригонометричних функцій; формування умінь знаходити періоди функцій У = sin (kx + b), у = cos (kx + b), У = tg (kx + b), у = ctg (kx + b). І. Перевірка домашнього завдання 1. Побудуйте на одиничному […]...
- Числові нерівності. Доведення числових нерівностей УРОК № 2 Тема. Числові нерівності. Доведення числових нерівностей Мета уроку: домогтися засвоєння учнями змісту: додаткових нерівностей для суми взаємно обернених додатних чисел та середнього арифметичного двох невід’ємних чисел (у порівнянні з їх середнім геометричним) та доведення цих нерівностей; способу застосування доведених нерівностей при доведенні інших числових нерівностей. Продовжити роботу з вироблення вмінь: відтворювати зміст […]...
- Довжина кола і дуги кола УРОК № 20 Тема. Довжина кола і дуги кола Мета уроку: виведення формул для знаходження довжини кола та довжини дуги кола. Формування вмінь учнів застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Довжина кола і площа круга” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють формули довжини кола і […]...
- Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
- Зображення нерівностей земної поверхні на плані та карті РОЗДІЛ 2 ЗЕМЛЯ НА ПЛАНІ ТА КАРТІ Тема 1. Способи зображення Землі § 17. Зображення нерівностей земної поверхні на плані та карті Пригадайте Як ви зображували нерівності поверхні на своїх дитячих малюнках? Лінії рівних висот. Зовсім плоскі ділянки земної поверхні трапляються дуже рідко. Земна поверхня здебільшого нерівна і складається з опуклих й увігнутих ділянок, різноманітних […]...
- Розв’язування систем рівнянь Математика – Алгебра Розв’язування систем рівнянь Розглянемо системи рівнянь, в яких одне або обидва рівняння другого степеня. 1. Щоб розв’язати систему рівнянь графічним способом, треба побудувати в одній системі координат графіки обох рівнянь системи й знайти координати точок перетину графіків. Ці точки і будуть розв’язками системи рівнянь. Наприклад: Графіком першого рівняння є коло з центром […]...
- Перетворення графіків функцій – Функції та графіки Математика – Алгебра Функції та графіки Перетворення графіків функцій 1. Графіки функцій і є симетричними відносно осі Ox. 2. Щоб побудувати графік функції , треба графік функції розтягнути від осі Ox в k разів, якщо , або стиснути його в k разів до осі Ox, якщо . 3. Щоб побудувати графік функції , треба графік […]...