Кут між прямою і площиною
Урок 54
Тема. Кут між прямою і площиною
Мета уроку: формування поняття кута між прямою і площиною, а також умінь учнів знаходити кути між прямою і площиною.
Обладнання: стереометричний набір, модель куба.
Хід уроку
1. Фронтальне опитування.
1) Дайте означення кута між мимобіжними прямими.
2) Чи залежить кут між мимобіжними прямими від вибору прямих, які перетинаються і паралельні даним мимобіжним прямим?
3) Сформулюйте узагальнене означення перпендикулярності прямої і площини.
4) Сформулюйте узагальнену ознаку
5) Сформулюйте узагальнену теорему про три перпендикуляри.
2. Перевірка розв’язування задачі № 32.
Спроектуємо ортогональне прямі а, b, с на площину, яка паралельна їм, одержимо прямі а1, b1, с1 відповідно, які попарно перетинаються і паралельні прямим а, b, с. Можливі два випадки (рис. 279).
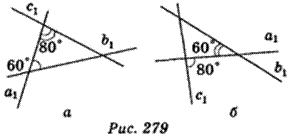
У випадку “а” маємо: кут між прямими b1 і с1 дорівнює 180° – 60° – 80° = 40°.
У випадку “б” маємо: кут між прямими b1 і с1 дорівнює 180° – (180° – 80°) – 60° = 20°.
А через те що b || b1, с || c1, кут між прямими b і с може дорівнювати або 40°, або 20°.
Відповідь.
3. Розв’язування задач.
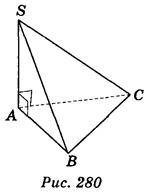
1) Грані SAB і SAC тетраедра SABC (рис. 280) – прямокутні трикутники з прямим кутом з вершиною в точці А. Доведіть, що ребра ВС і AS взаємно перпендикулярні.
2) Дано куб ABCDA1B1C1D1. Доведіть, що площина, яка проходить через точки А, В1, D1, перпендикулярна до діагоналі А1С.
У курсі геометрії 10 класу ми розглянули випадки розміщення прямої і площини: 1) пряма лежить у площині; 2) пряма паралельна площині; 3) пряма перпендикулярна до площини. Залишається дослідити випадок, коли пряма перетинає площину, але не перпендикулярна до неї.
Такі прямі можуть бути нахилені до площини під різними кутами. Що ж розуміють під кутом між прямою і площиною?
Якщо пряма паралельна площині або належить їй, то вважають, що кут між прямою і площиною дорівнює 0°. Якщо пряма перпендикулярна до площини, то кут між ними дорівнює 90°. У решті випадків кутом між прямою і площиною називають кут між прямою і її проекцією (ортогональною) на площину. На рис. 281 ВС
?, А – точка перетину прямої а з площиною?, тоді кут між прямою а і площиною? дорівнює куту ВАС = ?. Якщо? – кут між прямою і площиною, то 0° 
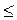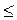? 90°.
Розв’язування задач
1. Задача № 35 із підручника (с. 56).
2. Дано зображення куба. Знайдіть кут між площиною АВС і прямою а (рис. 282).
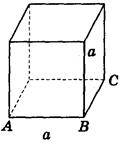
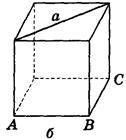
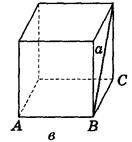
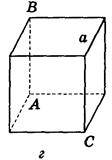
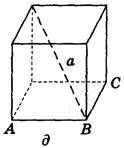
Рис. 282
(Відповідь, а) 90° ; б) 0°; в) 45° ; г) 45° ; д) arctg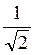 
).
3. Задача № 37 із підручника (с. 57).
4. Задача № 39 із підручника (с. 57).
5. Задача № 41 із підручника (с. 57).
6. Задача № 34 із підручника (с. 56).
§4, п. 32; контрольне запитання № 15; задачі № 36, 38, 40 (с. 57).
Запитання до класу
1) Дайте означення кута між прямою і площиною.
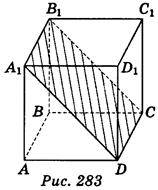
2) У кубі ABCDA1B1C1D1 проведено переріз січною площиною, яка проходить через точки А1, D, С (рис. 283). Укажіть, які з наведених тверджень правильні, а які – неправильні:
А) площина A1DB1 перпендикулярна до прямої АА1;
Б) кут між прямою AD і площиною A1DC, дорівнює 45°;
В) кут між прямою АВ і січною площиною дорівнює 0°;
Г) кут між прямою BC1 і площиною A1DC дорівнює 90°.
(1 votes, average: 5.00 out of 5)
Loading...