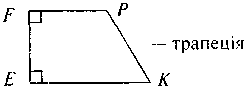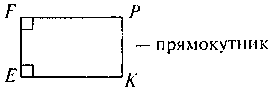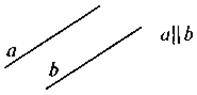Паралельні прямі
Урок № 109
Тема. Паралельні прямі
Мета: сформувати уявлення про зміст поняття “паралельні прямі”; виробити вміння знаходити на рисунку паралельні прямі та будувати за допомогою косинця і лінійки пряму, паралельну до даної, що проходить через точку поза даною прямою.
Тип уроку: засвоєння нових знань.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
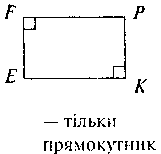
@ Перевіряємо найбільш цікаве завдання 3 з домашньої роботи і коментуємо наведені рисунки:
1) | 2) | 3) |
|
| |
|
@ Бажано прокоментувати два випадки: вид чотирикутника залежить не тільки від кутів, але й від співвідношення між сторонами чотирикутника.
III. Актуалізація опорних знань
1. Серед прямих, зображених на рисунку, знайдіть пари перпендикулярних прямих.
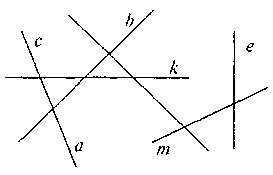
2. а якому з рисунків показано, як правильно побудувати пряму b, перпендикулярну до прямої а через т. А.
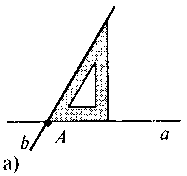
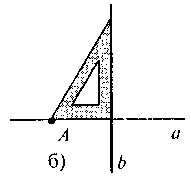
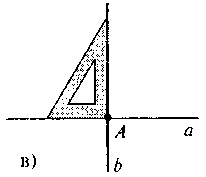
3. Чи можуть дві прямі:
А) перетинатись в одній точці;
Б) перетинатись удвох точках;
В) не перетинатись (не мати спільних точок)?
IV. Формування знань
@ Зважаючи на вік шестикласників та рівень їх математичної підготовки, означення паралельних прямих даємо на наочно-конкретному рівні (тобто йдемо від прикладів до означення, причому факт належності двох паралельних прямих одній площині проговорюємо, але не дуже зосереджуємося на цьому факті).
План викладення матеріалу
1. Приклади з навколишнього середовища, що дають уявлення про паралельні прямі.
2. Означення паралельних прямих, паралельних відрізків.
3. Властивість паралельних (перпендикулярних) прямих.
4. Побудова прямої, що проходить через точку поза даною прямою паралельно до даної прямої.
1. Звичайно, приклади з життя, які можуть бути пов’язані з уявленням
про паралельні прямі, учням добре знайомі: це рельси; відбиток полоззя санок; відбиток автомобільних шин на прямолінійному відрізку шляху і т. ін. Зрозуміло, що всі ці приклади лише ілюструють поняття паралельних прямих.
2. Означення паралельних прямих:
Дві прямі площини, що не мають спільних точок, називаються паралельними.
При цьому слід показати, що найпростіше зобразити дві паралельні прямі за допомогою лінійки (див. рис.), провівши дві прямі з обох боків лінійки, не відриваючи лінійки від аркуша.
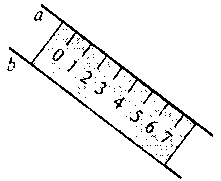
Зауваження. Для короткого способу позначення паралельних прямих, також як і для перпендикулярних прямих, використовуємо спеціальну позначку (символ); на рисунку а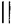 
b.
(Для допитливих учнів, якщо виникне таке питання, можна показати дві прямі, що не мають спільних точок, але не лежать в одній площині, за допомогою імпровізованих моделей прямих – двох ручок); але загострювати увагу не варто, бо учні мають не досить розвинену просторову уяву прямих, що “належать одній площині”, або не зрозуміють чи зрозуміють неправильно, а це відбере час на уроці.)
Так само, як і під час вивчення теми “Перпендикулярні прямі”, разом із поняттям паралельних прямих розглядаємо поняття “паралельних відрізків” як таких, що лежать на паралельних прямих (або відрізки паралельних прямих).
У програмі не передбачено вивчення властивостей паралельних прямих, але автор вважає за доцільне принаймні дві з них розглянути, бо вони є основою для розв’язування задачі на побудову прямої, паралельної даній, яка проходить через дану точку поза даною прямою. Такими властивостями є:
А) через точку, що не лежить на даній прямій, можна провести тільки одну пряму, паралельну до даної;
Б) якщо дві прямі перпендикулярні до третьої, то вони між собою не паралельні.
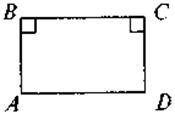
Приклад: у прямокутнику ABDC сторони АВ і CD перпендикулярні до ВС, тому відрізки АВ і CD паралельні (прямі АВ і CD – паралельні).
АВ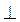
ВС, CD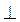BC, отже, AB 
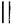CD.
3. З попереднього пункту випливає алгоритм побудови прямої, паралельної даній прямій, що про ходить через дану точку поза даною прямою. (Бажано прокоментувати побудову відповідно до запису у п. 3 (б).)
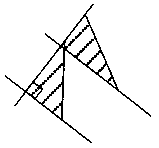
1) с
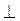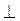А; 2) bC, cB (b проходить через т. А), отже, аС, bС i a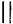
b. Усі записи і коментарі, які учні і вчитель виконують у ході пояснень у зошитах і на дошці, відповідно можуть мати вигляд конспекту 36.
Конспект 36 | |
Паралельні прямі | |
1. Якщо прямі а і b не перетинаються, то вони паралельні.
| 2. Якщо а
|
3. Через точку А, що не належить прямій а, можна провести єдину пряму b так, що а | |
| 1-й крок: провести с 2-й крок: провести через т. А пряму b, b 3-й крок: маємо: а |
V. Закріплення знань, вироблення вмінь
Усні вправи
1. Які з прямих на рисунку паралельні? Встановіть спочатку “на око”, а потім перевірте за допомогою лінійки та косинця.
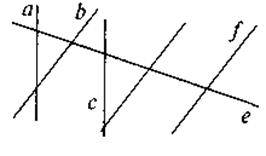
2. Наведіть приклади паралельних прямих на предметах, що вас оточують.
3. На рисунку 1 KLMN – прямокутник. Назвіть паралельні відрізки.
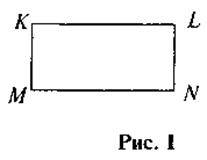
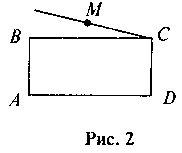
4. На рисунку 2 ABCD – прямокутник. Чи паралельні прямі МС i АD.
Письмові вправи
1. Через точку, що не належить прямій b, проведіть пряму с, паралельну до b.
2. Накресліть дві паралельні прямі а i b. На прямій а виберіть точки А i В. Проведіть із цих точок перпендикуляри до прямої b. Виміряйте довжини цих перпендикулярів та порівняйте їх.
@ Після виконання цього завдання доречно буде дати означення (яке не є обов’язковим для розгляду) відстані між двома паралельними прямими.
3. Накресліть трикутник ABC. Виміряйте довжину АВ та позначте середину сторони AB точкою D. Через точку D проведіть пряму, паралельну прямій АС. У якому відношенні ділить побудована пряма сторону ВС?
4. Сума двох чисел дорівнює 47. Одне з них більше від другого на 9. Знайдіть ці числа.
VI. Підсумки уроку
Ігровий момент
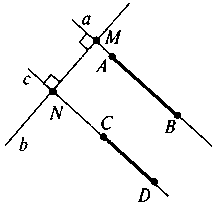
Учитель. Зараз ми перевіримо, чи добре ви засвоїли нові поняття та поняття, що були розглянуті на попередніх двох уроках. Виконаємо “німий диктант”. (На готовому рисунку, який виконано на відкидній дошці заздалегідь, учитель показує різні фрагменти, а учні повинні назвати ці фрагменти, використовуючи вивчену термінологію, і записати ці терміни в зошит), потім перевіримо записи і проведемо рефлексію “як я засвоїв поняття перпендикулярних та паралельних прямих”.
VII. Домашнє завдання
1. Доданої прямої а проведіть дві паралельні прямі b і с (b а та с 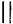а). Користуючись лінійкою і косинцем, переконайтеся, що b 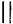с.
2. Накресліть прямокутник KLMN зі сторонами KL = 4 см і LM = 2 см. Через середину сторони KL проведіть пряму, паралельну до LM. Переконайтеся, що пряма ділить сторону навпіл.
3. Сума двох чисел дорівнює 13. Одне з них більше за інше на 25. Знайдіть ці числа.
(1 votes, average: 5.00 out of 5)
Loading...