Перпендикулярність прямих у просторі
Урок 25
Тема. Перпендикулярність прямих у просторі
Мета уроку: формування поняття про перпендикулярні прямі. Вивчення теореми про прямі, що перетинаються і паралельні двом перпендикулярним прямим.
Обладнання: стереометричний набір.
Хід уроку
В кінці уроку збираються учнівські зошити для перевірки їх ведення та виконання домашнього завдання.
III. Сприйняття й усвідомлення нового матеріалу
Означення перпендикулярних прямих у просторі
Поряд із відношенням паралельності в геометрії важливе значення має відношення
У стереометрії розглядають три випадки перпендикулярності: перпендикулярність прямих, перпендикулярність прямої і площини, перпендикулярність площин. На наступних уроках ми займемося послідовним вивченням цих трьох відношень. Почнемо з випадку перпендикулярності прямих у просторі.
Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
Розв’язування задач
1. Назвіть в оточенні моделі прямих,
2. Дано зображення куба АBСDA1B1C1D1. Укажіть ребра куба, які перпендикулярні до прямої АА1.
3. Задача № 3 (1, 4) із підручника (с. 34).
Теорема про прямі, що перетинаються і паралельні двом перпендикулярним прямим
Питання до класу: що можна стверджувати про взаємне розташування прямих а1 і b1, які перетинаються і а1 || а, b1 || b, а 
b? Учні висувають гіпотезу, що a1 B1. Для ілюстрації цього твердження використовується каркасна модель куба або прямокутного паралелепіпеда.
Далі формулюємо теорему:
Якщо дві прямі, які перетинаються, паралельні відповідно двом перпендикулярним прямим, то вони теж перпендикулярні.
Доведення цієї теореми проводить учитель. Подаємо запис доведення теореми, який рекомендується зробити на дошці і в зошитах учнів.
Дано: aB, а
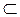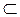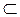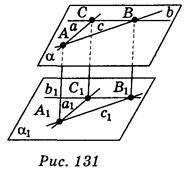
?, b?; а1||а, b1||b, а1?1, b1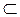?1, а1 і b, перетинаються (рис. 131).
Довести: а1 b1
Номер п/п | Твердження | Аргумент |
1 | А і b лежать в?, а1 і b1 лежать в?1 | Сз |
2 | А || а1 | Теорема 2.4 |
3 | Нехай точка С – точка перетину а і b, точка С1 – точка перетину а1 і b1 | Означення |
4 | AA1 || СС1, ВВ1 || CC1 | Теорема 2.1 |
5 | A1A2 || BB1 | Теорема 2.2 |
6 | CAA1C1 і CBB1C1 – паралелограми, отже, AC = А1С1, BC = B1C1 | AC||A1C1;AA1 || CC1, СВ || С1В1, ВВ1 || СС1 |
7 | АВB1А1 – паралелограм, отже, АВ = А1B1 | АВ||А1B1, AA1 || ВВ1 |
8 | ?АВС =?А1В1С1, отже, <A1C1B1= <ACB = 90°, тоді а1 | Третя ознака рівності трикутників |
Розв’язування задач
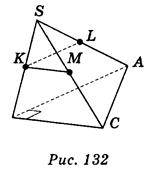
1. SABC – тетраедр; 
ABC = 90°; точки К, L, М – середини ребер SB, SA, SC відповідно (рис. 132). Знайти MKL.
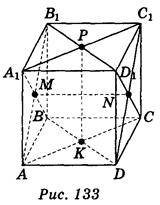
2. Дано зображення куба ABCDA1B1C1D1 (рис. 133). Точки М, N, Р, К – точки перетину діагоналей граней АВВ1А1, CDD1C1, А1B1С1D1 і ABCD відповідно. Довести, що MNРК.
3. Дано куб ABCDA1B1C1D1. Через точку М, що належить ребру АА1 в грані AA1DD1, проведіть пряму MN так, щоб MOD1 = 90°, де точка О – точка перетину прямих MN і AD1.
Розв’язання
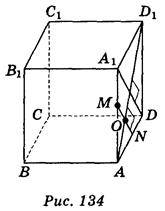
Проведемо в квадраті A1ADD1 діагоналі AD1 і A1D (AD1A1D) (рис. 134). Через точку М ребра АА1 в грані АDD1А1 проведемо пряму MN || А1D. За теоремою 3.1 MNAD1, оскільки A1OD1 = 90°.
4. Дано куб ABCDA1B1C1D1. Через точку О грані А1АDD1 проведіть прямі ОМ і ON так, щоб ОМ || ВС, ON || СС1. Доведіть, що MON = 90° .
5. Через точку О перетину діагоналей куба ABCDA1B1C1D1 проведіть площину?, паралельну основі А1B1С1D1 куба. Доведіть, що MON = 90°, де точки М, N – точки перетину ребер СС1 і BВ1 з площиною?.
IV. Домашнє завдання
§3, п. 14; контрольні запитання № 1, 2; задача № 3 (2; 3) (с. 34).
V. Підведення підсумку уроку
Запитання до класу
1) Які прямі в просторі називаються перпендикулярними?
2) Чи визначають площину дві перпендикулярні прямі? Чому?
3) Сформулюйте теорему про прямі, які перетинаються і відповідно паралельні перпендикулярним прямим.
4) Сторони двох трикутників відповідно паралельні. Чи паралельні відповідні висоти цих трикутників?
5) Ребро куба дорівнює а. Знайдіть довжину діагоналі грані куба. (Відповідь. а
)
6) Довжина діагоналі грані куба дорівнює а. Знайдіть ребро куба. (Відповідь.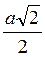 
)
(1 votes, average: 5.00 out of 5)
Loading...