Теорема Гульдіна
1379.
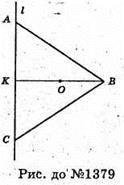
У трикутнику ABC AB = ВС, AC = a, BK + AC, BK = h.
Центром мас трикутника ABC є точка O – точка перетину медіан трикутника ABC: 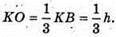 Тоді
Тоді 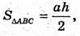
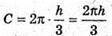 і
і 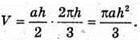
Відповідь: 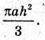
1380.
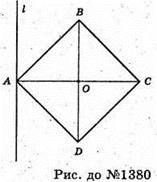
ABCD – ромб, AB = a, ∠BAD = a, BD? I. SABCD = AB2 sin∠BAD = а2 sin α.
Центром мас ромба ABCD є точка O перетину його діагоналей,
Тоді із ΔABO маємо: 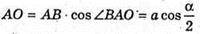 І
І 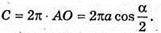
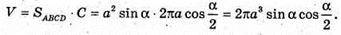
Відповідь:
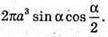
1381.
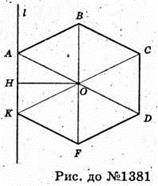
ABCDFK – правильний шестикутник, AB = а = = 27 см,
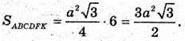
Центром мас правильного шестикутника е точка перетину його діагоналей.
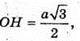
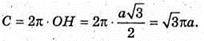
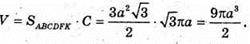
Якщо а = 27 см, то 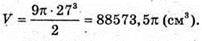
Відповідь: 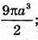 88573,5π см3.
88573,5π см3.
1382.
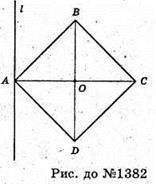
ABCD– квадрат, AC + l, AC = d.
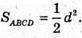 Центром мас квадрата ABCD є точка O перетину діагоналей.
Центром мас квадрата ABCD є точка O перетину діагоналей.
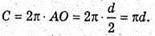
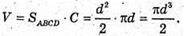
Відповідь: 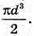
1383 .
Щоб довизначити задачу слід вказати, чи лежить вісь у площині квадрата.
1384.
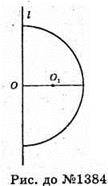
Знайдемо об’єм кулі, використовуючи теорему Гульдіна.
Нехай O1- центр мас півкола, тоді 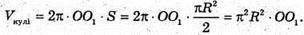
З іншого боку 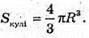 Тоді
Тоді 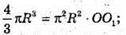
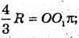
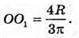
Відповідь: 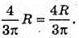
1385.
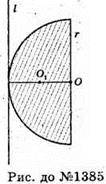
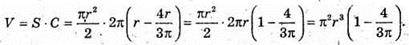
Відповідь: 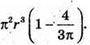
1386.
V = S × C = πг2 × 2πг = 2π2r3. Якщо г – 25, то V = 2π2×253 = 31 250π2(см3).
Відповідь: 2π2r3 = 31 250π2(см3).
1387.
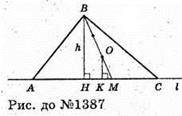
Розглянемо випадок обертання трикутника ABC навколо сторони АС.
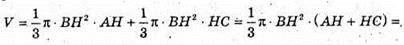
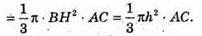
Враховуючи, що O – центр мас трикутника, то 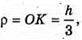 Звідси h = 3ρ.
Звідси h = 3ρ.
Тоді 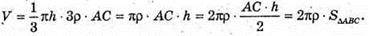
Отже, теорема доведена.
1388.
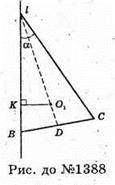
AB = AC = b, ∠BAC = α. 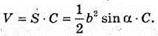
Проведемо AD + BC:
Із ΔABD: 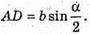
Оскільки O1- точка перетину медіан трикутника ABC, то
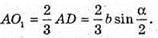
Проведемо O1K + l, тоді із ΔAO1K:
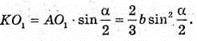
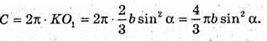
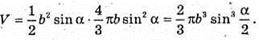
Відповідь: 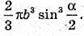
1389.
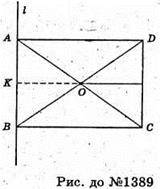
Нехай AB = a, AD = b, 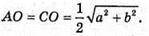
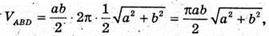
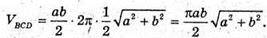
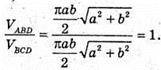
1390.
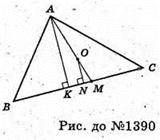
В трикутнику ABC AB = с, AC = b, BC = а,
O – точка перетину медіан трикутника. S – площа трикутника ABC.
Нехай AM – медіана трикутника ABC, проведемо ON + BC, AK + BC,
Тоді ΔAKM ~ ΔONM, тоді 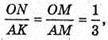 тоді
тоді 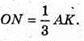
Отже, відстань від точки O до сторони трикутника дорівнює третині висоти трикутника, проведеної до цієї сторони.
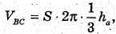
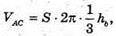
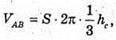
Де ha, hb, hc – висоти проведені до сторін а, b, с, тоді 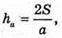
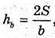
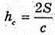
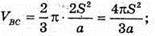
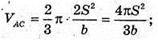
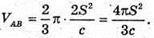
Звідси 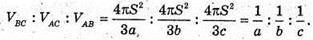
Відповідь: 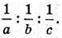
1391.
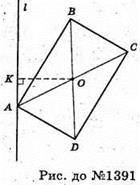
Оскільки SABCD = S, тоді 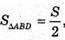 з іншого боку,
з іншого боку,
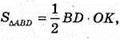
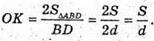
Тоді шуканий об’єм 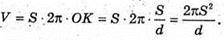
Відповідь: 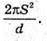
1392.
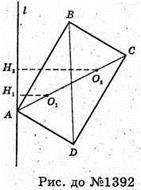
ABCD – паралелограм, AK? BD.
Нехай SΔABD = S, тоді SΔBCD = S, O1 і O2- центри мас трикутників ABD і BCD і
O1H1 + AK, O2H2 + АК, тоді (згідно з результатом задачі 1390) 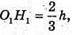
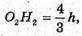
Де h – висота трикутника ABD.
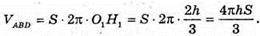
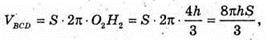
Тоді 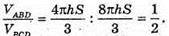
Відповідь: 1:2.
1393.
Оскільки 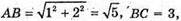
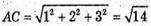
І AB2 + BC2 = AC2, то ΔABC – прямокутний (АС – гіпотенуза).
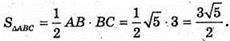
Нехай O – центр мас трикутника ABC.
А)
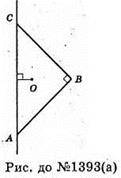
Враховуючи розв’язання задачі 1390, маємо:
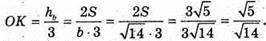
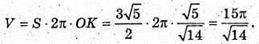
Відповідь: 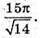
Б)
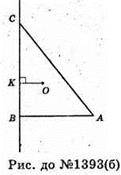
Враховуючи розв’язання задачі 1390, маємо:
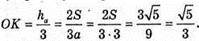
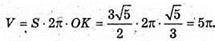
Відповідь: 5π.
1394.
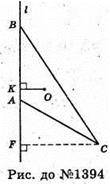
AB = a, ∠ABC = α, ∠BAC = 90 + α. O – центр мас, точка перетину медіан трикутника ABC, OK + AB, CF + AB. FC = BC sin∠ABC = a sin α, тоді
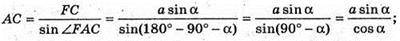
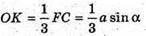
(див. розв’язання задачі 1390).
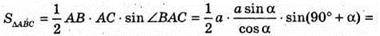

Тоді 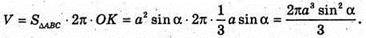
Якщо а = 18 дм, α = 41°, тоді
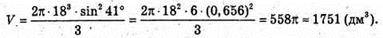
Відповідь: 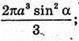 π 1751 дм3.
π 1751 дм3.
1395.
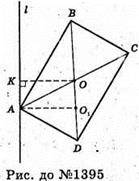
ABCD – прямокутник, BD? l, BD = d, ∠ADB = α.
Із ΔABD: AD = BD × cos∠ADB = d cos α; AB = BD × sin∠ADB = d sin α,
Тоді SABCD = AD × AB = d2 sin α cos α. OK + l, AO1+ l,
Тоді AO1 = AD × sin∠ADB = d cos × sin α,
Звідси KO = d cos α sin α.
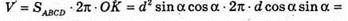
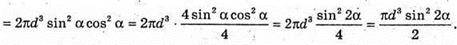
Відповідь: 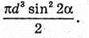
1396.
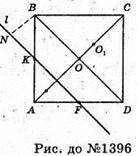
ABCD – квадрат, AS = a, AK = KB, AF = FD. Шуканий об’єм дорівнює сумі об’єму V1циліндра з твірною BD і радіусом основи OM без об’ємів двох конусів з твірною BK і радіусом основи MO та об’єму V2тіла обертання трикутника BCD навколо l.
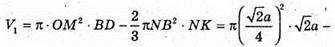
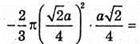
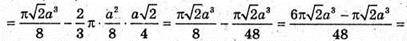
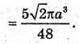
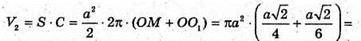
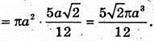
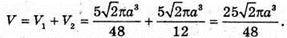
Відповідь: 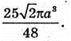
1397.
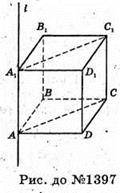
Шуканий об’єм дорівнює об’єму тіла утвореного обертання прямокутника
AA1C1C навколо AA1. Оскільки AB = а, тоді 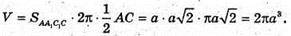
Відповідь: 2πα3.
1398.
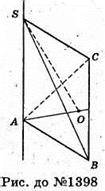
Шуканий об’єм дорівнює об’єму тіла, утвореного обертанням трикутників SCA і ACB навколо SA:
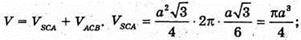
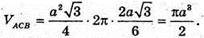
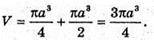
Відповідь: 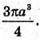
1399.
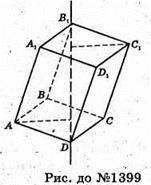
Нехай а – ребро куба, тоді
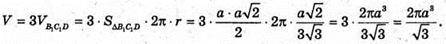
Враховуючи, що 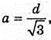 тоді
тоді 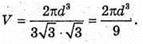
Відповідь: 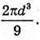
§ 36. Площі поверхонь
1410.
Знайдемо площу поверхні кулі з діаметром 8 см: S1 = 4π × φ2= 64π (см2), а також площу поверхні 15 куль діаметром 2 см: S2 = 15 × 4π × 12 = 60π (см2). Отже, на нікелювання однієї кулі діаметром 8 см витрачається матеріалу більше, ніж на нікелювання 15 куль діаметром 2см.
1411.
Перетворимо рівняння сфери: x2 – 4x + у2 + 2у + z2 = 4;
(х2 – 4х + 4) + (y2 + 2у + I) + z2 = 4 + 5; (х – 2)2 + (у + 1)2 + z2 = 9.
Отже, радіус сфери r = 3, тоді S = 4πг2 = 4π × 9 = 36π.
Відповідь: 36π.
1412.
Знайдемо довжину діаметра АВ:
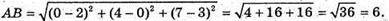
Отже, радіус сфери г = 3, тоді S = 4πг2 = 4π × 9 = 36π.
Відповідь: 36π.
1413.
Знайдемо радіус сфери:
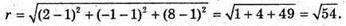
Отже, площа сфери S = 4πг2 = 4π × 54 = 216π.
Відповідь: 216π.
1414.
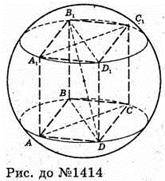
Нехай радіус сфери, вписаної в куб, дорівнює г. Тоді S = 4πг2, оскільки сфера вписана в куб, то ребро куба а дорівнює діаметру сфери: а = 2г.
Звідси 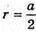 і
і 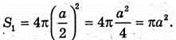
З ΔABD: BD2 = AB2 + AD2= 2а2.
З ΔB1BD: 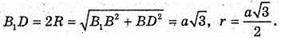
Отже, площа поверхні сфери, описаної навколо квадрата,
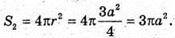
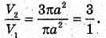
Відповідь: 1 : 3.
1415.
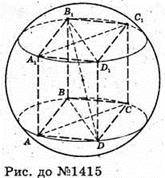
Оскільки прямокутний паралелепіпед вписаний у сферу,
То B1D = 2г, AB = 3 дм, BC = 4 дм, BB1 = 5 дм.
З Δ ABD: BD2 = AB2 + AD2 = 9 + 16 = 25 (дм).
З Δ BBD: 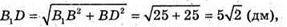
Звідси 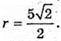
Отже, площа поверхні сфери S дорівнює
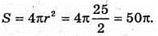
Відповідь: 50π дм2.
1416.
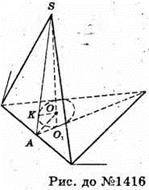
SA – апофема правильної піраміди, ∠ SAO1= α.
Центр O сфери, вписаної в піраміду, лежить на висоті SO1.
Нехай куля дотикається до деякої бічної грані в точці К,
Яка лежить на апофемі SA.
3 Δ SAO1: AO1 = AS × cos ∠ SAO1 = m × cos α.
ΔKOA = Δ O1OA (за катетом і гіпотенузою: KO = OO1, AO – спільна гіпотенуза).
Звідси: 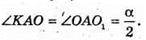
З Δ OA1A: 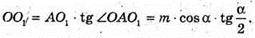
Отже, площа сфери S дорівнює:
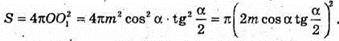
Обчислимо при m = 15, α = 60°:
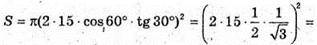
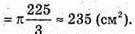
Відповідь: ≈ 235 см2.
1417.
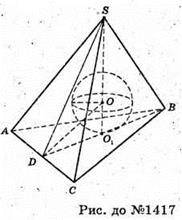
Нехай SABC – правильна трикутна піраміда, AB = BC = CA = а.
З вершини S проведемо SD + АС, оскільки Δ SAC – рівнобедрений, то SO – медіана, бісектриса і висота. В ΔABC проведемо BD + АС, тоді BD – бісектриса, медіана і висота. ∠SDO1= α.
Нехай г – радіус вписаної кулі. Проведемо OK + SD. OO 1 = OK = r.
ΔOKD ~ Δ ΟΟ1D.
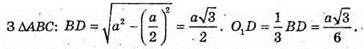
Тоді з ΔΟΟ,Ο: 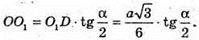
Отже, площа поверхні кулі V дорівнює:
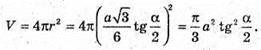
Відповідь: 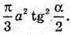
1418.
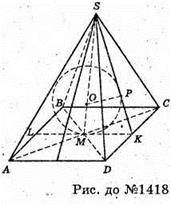
Нехай SABCD – задана чотирикутна піраміда, O – центр вписаного кола,
SO : OM = 5 : З, SO = 5х, OM = 3х,
В точках M і P куля дотикається основи і бічної сторони, отже, OA + LK,
OP + SK.
ΔSMK ~ ΔSOP. З подібності трикутників маємо:
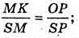
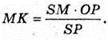
Знайдемо SP з ΔSOP: 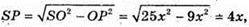
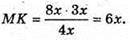
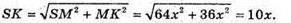
Отже, площа поверхні кулі S1 = 4π × 9х2 = 36πг2,
Площа бічної поверхні піраміди
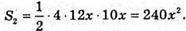
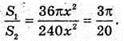
Відповідь: 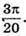
1419.
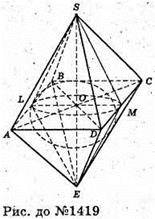
Нехай SABCDE – правильний октаедр, AB = BC = CD = DA = SA = … AE = а.
У ΔSCD: SM + DC, 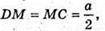 тоді з ΔSMD:
тоді з ΔSMD: 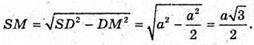
Площа поверхні октаедра 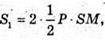 де P – периметр ABCD.
де P – периметр ABCD.
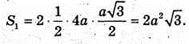 За умовою
За умовою 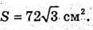 Отже,
Отже, 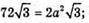
А2 = 36; а = 6 (см), тоді 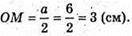
Площа поверхні сфери S2дорівнює: S2 = 4π × OM2 = = 4π × 9 = 36π (см2).
Відповідь: 36π см2.
1420.
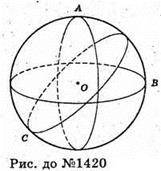
Нехай OA + OB, OB + ОС, ОС + ОА.
Площа поверхні частини кулі, обмеженої площинами АОВ, BOC і СОА,
Дорівнює 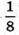 площі поверхні кулі, отже,
площі поверхні кулі, отже, 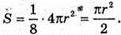
Відповідь: 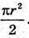
1421.
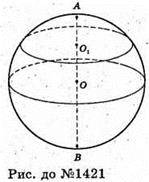
Нехай 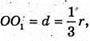 тоді
тоді 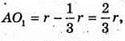
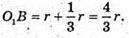
S 1 – площа першого сферичного сегмента:
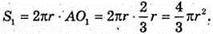
S2 – площа другого сферичного сегмента:
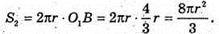
Відповідь: 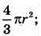
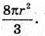
1422.
Площа поверхні кульового сегмента S = 2πrh = 2πr × 0,5г = πг2.
Відповідь: πг2.