Існування площини, паралельної даній площині
Урок 17
Тема. Існування площини, паралельної даній площині
Мета уроку: вивчення теореми про існування єдино! площини, яка паралельна даній площині і проходить через дану точку, що не належить даній площині.
Обладнання: стереометричний набір.
Хід уроку
Перевірка правильності розв’язування задачі № 25.
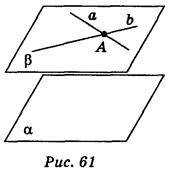
Через дану точку А проведемо дві довільні прямі а і b, паралельні площині а (рис. 61). Прямі а і b визначають площину b. Площина b паралельна площині a.
Будь-яка пряма с, яка проходить через точку А і паралельна площині a, лежить
Запитання до класу щодо розв’язання задачі № 25.
1) На підставі чого можна стверджувати, що прямі а і b визначають площину b?
2) Скільки площин можна провести через прямі а і b?
3) Поясніть, чому площина b паралельна площині a.
4) На підставі чого можна стверджувати, що пряма с, якщо перетинає площину b, то перетинає і площину a?
II. Сприйняття й усвідомлення нового матеріалу
Теорема про існування площини, що паралельна даній площині
Перед вивченням нового матеріалу доцільно
При обговоренні звернути увагу учнів на розгляд двох випадків: 1) дана точка належить даній площині; 2) дана точка лежить поза даною площиною.
Далі повідомляється тема і формулюється теорема.
Теорема.
Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну.
Доведення розіб’ємо на дві частини.
1. Доведемо, що через точку поза даною площиною можна провести площину, паралельну даній площині.
Наводимо зразок запису доведення першої частини на дошці.
Дано: a, А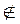 
a (рис. 62).
Довести: існує b, b || a, А I b.
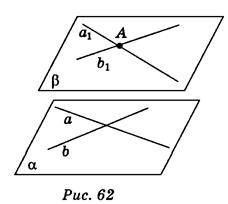
Проводимо в площині а дві прямі а і b, які перетинаються.
Через точку А проведемо прямі а1 і b1 такі, що а1 || а, b1 || b (теорема 2.1).
Через прямі а1 і b1 проведемо площину b, яка паралельна a (теорема 2.4).
Звертаємо увагу учнів на те, що безпосередньо з доведення існування площини b не випливає, що b – єдина, бо прямі а і b вибрані довільно, тому може статися, що другій парі таких прямих буде відповідати друга площина b1, паралельна а.
2. Доведемо, що через точку поза даною площиною проходить тільки одна площина, паралельна даній площині. Наводимо зразок запису доведення другої частини на дошці.
Дано: a, А 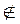a, b, b || a, А 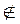b (рис. 63).
Довести: b – єдина.
Припустимо, через точку А проходить b1 така, що b1 || a.
Візьмемо точку С таку, що С I b1, С 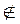b.
Візьмемо точку В, В I a.
Через точки А, B, С проведемо?, яка перетинає a по прямій b, b – по а, b1 – по с.
Тоді а || b, с || b. Отже, через точку А проходять дві різні прямі а і с, які паралельні прямій b, що суперечить теоремі 2.1.
Виконання вправ
1. Через пряму а, яка паралельна площині a, проведіть площину, паралельну даній площині a. Скільки площин можна провести?
2. Задача № 23 із підручника (с. 20).
3. Доведіть, що якщо площина? перетинає одну з паралельних площин a або b, то вона перетинає і другу площину.
4. Доведіть, що через будь-які мимобіжні прямі можна провести єдину пару паралельних площин.
§2, п. 11; контрольне запитання № 9; задача № 24 (с. 20).
Запитання до класу
Скільки площин, паралельних даній площині, можна провести через точку, яка:
А) належить даній площині;
Б) не належить даній площині?
(1 votes, average: 5.00 out of 5)
Loading...