Розв’язування задач на застосування ознаки перпендикулярності прямої і площини
Урок 28
Тема. Розв’язування задач на застосування ознаки перпендикулярності прямої і площини
Мета уроку: формування вмінь учнів застосовувати означення та ознаку перпендикулярності прямої і площини до розв’язування задач.
Обладнання: стереометричний набір, модель куба.
Хід уроку
І. Перевірка домашнього завдання
1. Перевірка правильності розв’язання задачі № 7 за записами (з пропусками), зробленими на дошці до початку уроку.
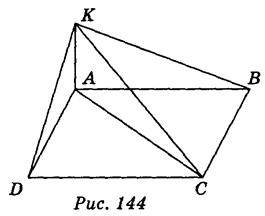
Розв’язання задачі № 7
Нехай ABCD – прямокутник; КА…(АВС);
KB = 7 м, КС
Із? КВА АВ =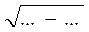 
= 
= 
.
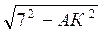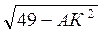Із? КAD AD =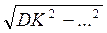 
= 
.
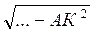Із? АСD AC2 = AD2 + DC2 = AD2 +… = 36 – АК2 + + 49 – АК2 = … – 2АК2.
Із? АСK КС2 = АК2 + АС2; … = АK2 + 85 – АК2; АК2 = 85 – …; АК2 = 4 ; АК = 2 (м). Відповідь. 2 м.
2. Математичний диктант.
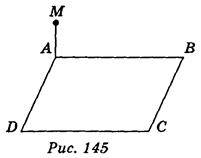
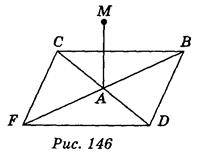
Відрізок МА перпендикулярний до площини АВС:
Варіант 1 – прямокутника ABCD (рис. 145);
Варіант 2 – ромба CBDF (рис. 146), в якому АВ = 3 см, AD = 4 см, МА = 1 см.
Користуючись зображенням, знайдіть:
1) відстань між
2) довжину відрізка MD; (2 бали)
3) відстань між точками А і С; (2 бали)
4) довжину відрізка BD; (2 бали)
5) відстань між точками М і С; (2 бали)
6) площу трикутника МАС. (2 бали)
Відповідь. Варіант 1. 1)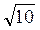 
См; 2) 
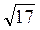См; 3) 5см; 4) 5 см; 5) 
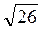См; 6) 2,5 см2.
Варіант 2. 1) 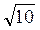См; 2) 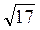См; 3) 4 см; 4) 5 см; 5) 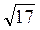См; 6) 2 см2.
1. Три промені ОА, ОВ і ОС попарно перпендикулярні. Як розташований кожний із променів відносно площини, яка визначається двома іншими променями?
2. Через точку О перетину діагоналей квадрата зі стороною а проведено пряму ОК, перпендикулярну до площини квадрата. Знайдіть відстань від точки К до вершин квадрата, якщо OK = b.
(Відповідь.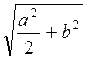 
)
3. У трикутнику АВС 
C = 90°, AC = 6 см, ВС = 8 см, CM – медіана. Через вершину С проведено пряму СК, яка перпендикулярна до площини трикутника АВС, причому СК =12 см. Знайдіть KM.
(Відповідь. 13 см)
4. Пряма CD перпендикулярна до площини правильного трикутника АВС. Через центр О цього трикутника проведена пряма ОК, паралельна до прямої CD. Відомо, що АВ = 16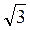
См, ОК = 12см, CD = 16см. Знайдіть відстань від точок D і К до вершин А і В трикутника.
(Відповідь. КА = КВ = 20 см; DA = DB = 32 см)
5. Ребро куба дорівнює а. Знайдіть відстань від точки перетину діагоналей однієї із граней до вершин протилежної їй грані.
(Відповідь.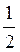 
A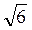
)
6. Діагональ BD1 прямокутного паралелепіпеда ABCDA1B1C1D1 дорівнює d, діагональ AD1 грані дорівнює b. Знайдіть АВ.
(Відповідь.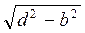 
)
7. Задача № 5 із підручника (с. 34).
III. Домашнє завдання
§3, п. 15; задача № 8 (с. 35).
IV. Підведення підсумку уроку
Запитання до класу
1) Дайте означення прямої, перпендикулярної до площини.
2) Сформулюйте ознаку перпендикулярності прямої і площини.
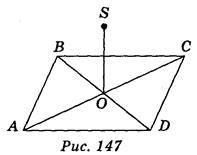
3) Відстань від точки S до кожної із вершин прямокутника ABCD однакова (рис. 147), точка О – точка перетину діагоналей АС і BD прямокутника ABCD. Укажіть, які з поданих нижче тверджень правильні, а які – неправильні:
А) пряма SO перпендикулярна до прямої BD;
Б) пряма SO не перпендикулярна до прямої АС;
В) пряма SO не перпендикулярна до площини АВС;
Г) пряма АС обов’язково перпендикулярна до площини BDS;
Д) якщо АВ = 6 cm; BC = 8 см і AS = 13 см, то SO = 12 cm.
4) Відстань від точки S до всіх вершин прямокутного трикутника АВС (C = 90°) однакова, точка О – середина гіпотенузи АВ. Укажіть, які з поданих нижче тверджень правильні, а які – неправильні:
А) пряма CO не може бути перпендикулярна до площини SAB;
Б) пряма CO обов’язково перпендикулярна до прямої SO;
В) пряма SO обов’язково перпендикулярна до площини АВС;
Г) якщо АС = 6 см, BC = 8 см і CS = 13 см, то SO = 12 см.