Векторний добуток векторів
1.
Векторний добуток векторів є вектором, а скалярний – числом.
Векторний та скалярний добуток мають однакові властивості (крім комутативності).
2.
За означенням модуля векторного добутку 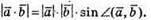
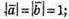
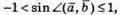
А отже, оскільки 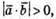 то
то 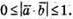
3.
1) 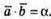 За означенням
За означенням 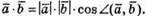
У нашому випадку 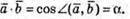
Скористаємось основною тригонометричною тотожністю:
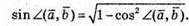
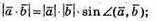
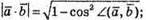
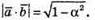
2) 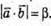 За означенням
За означенням 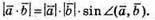
У нашому випадку 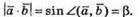
Скористаємось основою тригонометричною тотожністю:
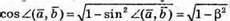 Тоді
Тоді 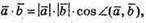
Оскільки 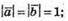
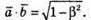
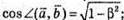
3) Рівність виконується, якщо 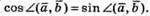
Тобто якщо кут між векторами дорівнює 45°.
4. За означеннями 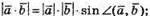
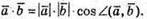
Маємо: 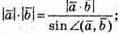
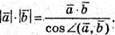
Порівняємо ці співвідношення.
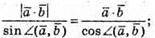
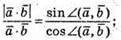
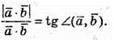
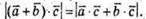
5.
Скористаємось тим, що 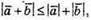 тоді маємо
тоді маємо 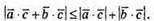
Геометричне тлумачення: площа діагонального перерізу прямого паралелепіпеда менша за суму площ двох його суміжних граней. Рівність виконується, якщо 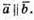
6.
1) 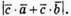
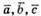 – одиничні вектори, що йдуть від центра правильного трикутника до його вершин, отже, кути між векторами становлять 120°.
– одиничні вектори, що йдуть від центра правильного трикутника до його вершин, отже, кути між векторами становлять 120°.
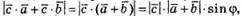 де φ – кут між векторами
де φ – кут між векторами 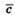 і
і 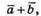 , а κуτ між ними становить 0°, а отже, sin 0° = 0. Тоді і векторний добуток дорівнює 0.
, а κуτ між ними становить 0°, а отже, sin 0° = 0. Тоді і векторний добуток дорівнює 0.
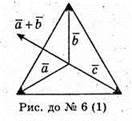
2) 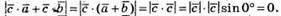
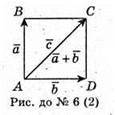
3) 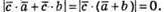
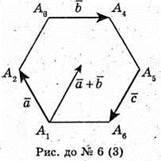
Оскільки вектори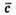 і
і 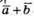 колінеарні
колінеарні
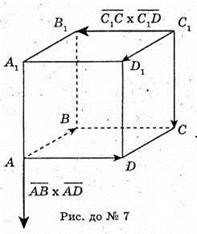
7.
Related posts:
- Скалярний добуток векторів Геометрія Вектори Скалярний добуток векторів Скалярним добутком векторів і називається число . Позначення: . . Очевидно, що . Розподільна властивість скалярного добутку: . Кутом між ненульовими векторами і називається кут BAC. Кутом між будь-якими двома ненульовими векторами і називається кут між векторами, що дорівнюють даним і мають спільний початок. Вважають, що кут між однаково напрямленими […]...
- Кут між векторами. Скалярний добуток векторів Урок 59 Тема. Кут між векторами. Скалярний добуток векторів Мета уроку: формування понять кута між векторами, скалярного добутку векторів. Формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі” Хід уроку 1. Фронтальна бесіда з класом за контрольними запитаннями № 18- 20 з використанням схеми “Вектори в просторі” (див. с. 233). […]...
- Скалярний добуток векторів УРОК № 49 Тема. Скалярний добуток векторів Мета уроку: формування поняття скалярного добутку векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: формулюють означення скалярного добутку, його властивості; застосовують вивчені означення та властивості до розв’язування […]...
- Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Урок 58 Тема. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами Мета уроку: формування знань учнів про вектори в просторі, дії над векторами, заданими координатами, Формування вмінь застосовувати вивчений матеріал до розв’язування задач. Обладнання: схема “Вектори в просторі”. Хід уроку І. Перевірка домашнього […]...
- Скалярний добуток векторів. Кут між векторами 233. А) Якщо то α = 90°, α – кут між векторами. Б) то α – гострий; А) то α – тупий. 234. А) Б) В) Г) 235. А) Б) 236. А) Б) В) Г) 237. А) Б) В) 238. α – кут між векторами А) Б) В) Г) 239. А) Звідси Б) Звідси В) […]...
- Розв’язування задач координатно-векторним методом 1. 1) Введемо прямокутну систему координат із початком у точці В і спрямуємо вісь Оx вздовж ребра BA, Oz – вздовж ВВ1. Довжину ребра куба позначимо як а. Тоді координати точок: А(а; 0; 0;); С(0; а; 0); R(а; а; 0); C1(0; а; а). Знайдемо координати векторів і Знайдемо довжини векторів: Знайдемо кут між векторами: Кут […]...
- Розв’язування задач на застосування векторів Урок 60 Тема. Розв’язування задач на застосування векторів Мета уроку: формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: стінна таблиця “Вектори в просторі”. Хід уроку І. Перевірка домашнього завдання 1. Два учні відтворюють розв’язування задач № 55 (4), 56. 2. Фронтальне опитування. 1) Чому дорівнює скалярний добуток векторів, які задано координатами? 2) Як […]...
- Алгебра векторів 1. Побудуємо вектори – одиничний вектор 2. Побудуємо вектори 3. Побудуємо вектори 4. Побудуємо вектори 5. 6. 1) Побудуємо вектори 2) Побудуємо вектори 7. Побудуємо вектори 8. 1) 2) 9. Побудуємо вектори Вектори та рівні. 10. Накреслимо два ненульові вектори Побудуємо Побудуємо Таким чином, 11. Побудуємо вектори Вектори протилежно напрямлені. 12. Побудуємо вектори 13. 1) […]...
- Координати вектора. Дії над векторами, що задані координатами 1. Запишемо координати вектора: 1) 2) 3) 4) 2. 1) 2) 3) 4) 5) 6) 3. 1) Запишемо розклад за координатними векторами: 2) Запишемо розклад за координатними векторами: 3) Запишемо розклад за координатними векторами: 4) Знайдемо координати векторів : Знайдемо координати вектора Запишемо розклад за координатними векторами: 5) Знайдемо координати векторів Знайдемо координати вектора Запишемо […]...
- Застосування векторів 269. 5(х – 2) + 0 × (у + 1) – 3(z – 4) = 0; 5x – 10 – Зz + 12 = 0; 5x – Зz + 2 = 0 – рівняння шуканої площини. 270. 3(x – 1) – 4(y – 2) + 7(z + 3) = 0; 3x – 3 – 4у […]...
- Додавання векторів Геометрія Вектори Додавання векторів Сумою векторів і називається вектор . Додавання векторів має переставну та сполучну властивості: ; для будь-яких , , . Теорема. Які б не були точки A, B, C, справджується векторна рівність: . Правило трикутника додавання векторів Щоб знайти суму довільних векторів і , треба від кінця вектора (див. рисунок) відкласти вектор […]...
- Додавання векторів УРОК № 44 Тема. Додавання векторів Мета уроку: формування вміння додавати вектори, вивчення властивостей суми векторів; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують додавання векторів; відкладають вектор, що дорівнює сумі векторів; формулюють […]...
- Вектори в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Вектори в просторі Усі основні означення векторів у просторі залишаються такими самими, як означення векторів на площині (див. розділ “Геометрія. 8 клас”). Координатами вектора , де , , називають числа, , . Вектори рівні тоді, й тільки тоді, коли вони мають відповідно рівні координати. Це дає підставу позначити […]...
- Віднімання векторів УРОК № 45 Тема. Віднімання векторів Мета уроку: формування вмінь віднімати вектори, вивчення властивостей різниці векторів; формування вмінь застосовувати вивчені означення та властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують віднімання векторів; відкладають вектор, що дорівнює різниці векторів; формулюють властивості […]...
- Вектор. Модуль і напрям вектора. Рівність векторів УРОК № 42 Тема. Вектор. Модуль і напрям вектора. Рівність векторів Мета уроку: формування понять вектора, модуля вектора, напряму вектора; рівності векторів; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують вектор, модуль і […]...
- Тотожно рівні вирази. Тотожності 132. 1) Переставна властивість додавання; 2) сполучна властивість додавання; 3) переставна властивість множення; 4) переставна властивість множення і додавання; 5) розподільна властивість множення. 133. 1) 2х – 12 = 2(х – 6) – тотожність; 2) а – b = -(b – а) – тотожність; 3) 3m + 9 = 3(m + 9) – не є […]...
- Додавання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри Векторні величини (вектори) – це величини, які характеризуються числовими значеннями і напрямом: Скалярні величини (скаляри) – це величини, які характеризуються лише числовим значенням. Вони можуть бути додатними та від’ємними й додаються алгебраїчно. 3.1. Додавання векторів Якщо вектори спрямовані вздовж однієї прямої або якщо вони паралельні, то результуючий вектор дорівнює алгебраїчній сумі […]...
- Розкладання вектора за координатними осями Геометрія Вектори Розкладання вектора за координатними осями Вектор називається Одиничним, якщо його абсолютна величина дорівнює одиниці. Одиничні вектори, які мають напрями додатних координатних півосей, називаються Координатними векторами, або Ортами (див. рисунок). Позначення: ; . Оскільки координатні вектори відмінні від нуля й неколінеарні, то будь-який вектор можна розкласти за цими векторами: ....
- Вектори у просторі – ВЕКТОРИ Формули й таблиці МАТЕМАТИКА ВЕКТОРИ Вектори у просторі Вектор – спрямований відрізок А – початок вектора В – кінець вектора Модуль вектора – довжина відрізка, який зображує вектор: ||. Два вектори рівні, якщо вони однаково спрямовані і мають рівні модулі. Координати вектора з початком у точці А(x1,y1,z1) і кінцем у точці В(х2,у2,z2). Рівні вектори мають […]...
- ДОВЕДЕННЯ ТОТОЖНОСТЕЙ Цілі: – навчальна: удосконалити вміння учнів доводити тотожності; – розвивальна: формувати вміння міркувати за аналогією; розвивати творчі здібності, кмітливість учнів; – виховна: виховувати упевненість у власних силах, уміння самоорганізовуватися, спостережливість; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ ______________________________________________________ ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ […]...
- Відрізок і його довжина § 1. Найпростіші геометричні фігури та їхні властивості 2. Відрізок і його довжина Практичні завдання 20. Точки С, D, Е належать відрізку AB, а точки F, M, K не належать відрізку АВ. 21. Утворилося три відрізки АВ, ВС, АС. 22. Точка С лежить між точками А і В, а точка D – між точками В […]...
- Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...
- Добуток різниці та суми двох виразів Рівняння коренів не має; Коренем рівняння є будь-яке число; Отже, значення виразу не залежить від значення змінної. 2) (2a – b)(2a + b) + (b – с)(b + с) + (с – 2а)(с + 2а) = 4а2 – b2 + b2 – с2 + с2 – 4а2 = 0. Отже, значення виразу не залежить від […]...
- Властивості степеня з натуральним показником. Добуток степенів з однаковою основою Урок № 21 Тема. Властивості степеня з натуральним показником. Добуток степенів з однаковою основою Мета: домогтися свідомого розуміння учнями властивості добутку степенів з однією основою та сформувати вміння перетворювати числові та буквені вирази з використанням цієї властивості. Тип уроку: засвоєння знань, умінь та навичок. Хід уроку I. Перевірка домашнього завдання (Зібрати зошити) II. Актуалізація, опорних […]...
- Колінеарні вектори УРОК № 48 Тема. Колінеарні вектори Мета уроку: формування поняття “колінеарні вектори”; вивчення властивості та ознаки колінеарних векторів; формування вмінь учнів застосовувати вивчені означення та властивості до розв’язування завдань. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують колінеарність векторів; застосовують вивчені означення та […]...
- Перетворення многочлена на квадрат суми або різниці двох виразів 624. а2 – 18а + 81 = (а – 9)2. 625. Тотожністю є рівність 2) а2 + 8аb + 16b2 = (а + 4b)2. 628. 1) Якщо у = -4, то у2 – 8у + 16 = (у – 4)2 = (-4 – 4)2 = 64. 2) Якщо с = -10, то с2 + 24с […]...
- Властивості степеня з натуральним показником Розділ 1. ЦІЛІ ВИРАЗИ & 4. Властивості степеня з натуральним показником Розглянемо властивості степеня з натуральним показником. Вираз а3а2 є добутком двох степенів з однаковими основами. Застосувавши означення степеня, цей добуток можна переписати так: А3а2 = (ааа) ∙ (аа) = ааааа = а5. Отже, а3а2 = а5, тобто a5 = а2 + 3. У той […]...
- Тотожність Розв’яжіть задачі 132. 1) Ні; 2) ні; 3) так. 133. 1) Ні; 2) ні; 3) так. 134. 1) Ні; 2) так. 135. Так. Наприклад: 12 = 12. 136. 1) Ні; 2) ні; 3) так; 4) ні; 5) так; 6) так, при а, с ≠ 0. 137. 1) Ні; 2) ні; 3) так; 4) так, 138. […]...
- Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...
- Добуток розчинності – Рівновага розчинності ХІМІЧНА РІВНОВАГА 3. Рівновага розчинності 3.2 . Добуток розчинності Якщо до насиченого розчину солі у воді ще додати цю ж сіль, то ця добавка випаде в нерозчинений осад. Якщо до нього додати сіль, що містить один з іонів розчиненої солі, то утвориться такий самий осад. Приклад. Якщо до насиченого розчину кальцій сульфату додати трохи кальцій […]...
- Відрізок. Вимірювання відрізків. Відстань між двома точками Розділ 1. Елементарні геометричні фігури та їхні властивості § 2. Відрізок. Вимірювання відрізків. Відстань між двома точками 13. На рисунку зображені відрізки: AB, AK, BK, ВМ. AK = 38 мм, MB = 12 мм. 14. На рисунку зображені відрізки: PC, PD, CD, PT. PC = 9 мм. PD = 31 MM. PT = 27 мм. […]...
- Суміжні та вертикальні кути § 1. Найпростіші геометричні фігури та їхні властивості § 4. Суміжні та вертикальні кути Практичні завдання 86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС. ∠АОВ – прямий, ∠COA – суміжний до кута АОВ. ∠BOC – тупий, ∠AOB – суміжний до кута ВОС. 87. ∠AOC і ∠COB – суміжні. 88. а) ∠ABD i ∠CBD; […]...
- Розкладання многочленів на множники 702. Перетворити його в добуток кількох виразів. 703. 1) ні; 2) ні; 3) так. 704. 1) ні; 2) так; 3) ні. 705. 1) ні; 2) ні; 3) так. 706. 1) ні; 2) ні; 3) так. 707. ні; 2) так; 3) ні. 708. ні; 2) ні; 3) так. Жодна з рівностей не є тотожністю. 1) ні, […]...
- Додавання векторів за правилом паралелограма – Елементи векторної алгебри 3. Елементи векторної алгебри 3.2. Додавання векторів за правилом паралелограма Щоб додати два вектори за правилом паралелограма, треба розмістити їх так, не змінюючи їх напряму, щоб вони виходили з однієї точки, й добудувати на кінцях векторів паралельні прямі. Діагональ одержаного паралелограма, проведена з точки, в якій суміщені початки обох векторів, є їх сумою....
- Віднімання векторів – Елементи векторної алгебри 3. Елементи векторної алгебри 3.3. Віднімання векторів Різницею двох векторів, спрямованих по одній прямій або паралельних один одному, є алгебраїчна різниця цих векторів. Щоб знайти різницю двох векторів, які мають різні напрями, треба розмістити обидва вектори так, щоб вони виходили з однієї точки. Потім сполучити кінці векторів вектором, спрямованим від від’ємника до зменшуваного. Цей вектор […]...
- Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...
- Розкладання многочлена на многочлени. Винесення спільного множника за дужки 437. 1) Якщо х = 4,32, то 6,32х – х2 = х(6,32 – х) = 4,32 • (6,32 – 4,32) = 4,32 • 2 = 8,64. 2) Якщо а = 1,5, b = -2,5, то а3 + а2b = а2(а + b) = 1,52 • (1,5 – 2,5) = 2,25 • (-1) = -2,25. 3) […]...
- Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...
- Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...
- Пропорція. Основна властивість пропорції Розділ 3 Відношення і пропорції §21. Пропорція. Основна властивість пропорції Відношення 12 : 3 і 20 : 5 рівні, оскільки їх значення дорівнюють 4. Тому можна записати рівність Рівність двох відношень називають пропорцією. Слово “пропорція” походить від латинського proportio, що означає “співрозмірність”, тобто певне відношення частин між собою. За допомогою букв пропорцію записують так: Ці […]...