Властивості паралельних площин
Урок 18
Тема. Властивості паралельних площин
Мета уроку: формування знань учнів про властивості паралельних площин.
Обладнання: стереометричний набір.
Хід уроку
І. Перевірка домашнього завдання
1. Один учень відтворює розв’язування задачі № 24, у цей час клас пише математичний диктант.
2. Математичний диктант.
Дано зображення куба: варіант 1 – рис. 64, варіант 2 – рис. 65.
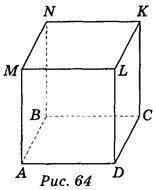
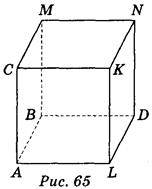
Користуючись зображенням, запишіть:
1) площину, яка паралельна площині АВС;
2) площину, яка паралельна площині СNL; (2 бали)
3) площину, яка паралельна площині МКD; (2 бали)
4) паралельні площини, які містять мимобіжні прямі МК і АВ; (2 бали)
5) паралельні площини, які проходять через мимобіжні прямі АВ і КD; (2 бали)
6) площину, яка паралельна площині МNК і містить пряму АD. (2 бали)
Відповідь.
Варіант 1. 1) МNК; 2) ВDМ; 3) АСN; 4) АВС і КLМ; 5) АВМ і СКD; 6) АВС.
Варіант 2. 1) LNК; 2) АDМ; 3) ВСL; 4) АВD і СКМ; 5) АВС і DКL; 6) АВD.
3. Перевірити математичний диктант та заслухати розв’язання задачі № 24.
II. Сприйняття й усвідомлення нового матеріалу
Запитання до класу
1) Знайдіть у класній
2) Покажіть лінії перетину цих площин третьою площиною.
3) Що можна сказати про взаємне розташування цих прямих? Далі формулюється теорема.
Теорема.
Якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні.
Цю теорему можна сформулювати по-іншому:
Доведемо теорему. Наводимо запис, який можна зробити на дошці і в зошитах учнів.
Дано: a || b; ? перетинає a по прямій а; ? перетинає b по прямій b.
Довести: а || b (рис. 66).
Припустимо, що а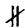
b. Оскільки а і b лежать в?, то вони перетинаються в деякій точці А; А I a, бо a I a; А I b, бо b I b. Отже, a і b перетинаються, що суперечить умові: a || b. Отже, а || b.
1. Паралельні площини a і b перетинають сторону АВ кута ВАС відповідно в точках А1 і А2, а сторону АС цього кута – відповідно в точках В1 і В2. Знайдіть:
А) АА2 і АB2, якщо А1А2 = 2А1А, А1А2 = 12 см, АВ1 = 5 см;
Б) А2В2 і АА2, якщо А1В1 = 18 см, АА1 = 24 см, АА2 =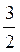 
А1А2.
(Відповідь, а) АА2 = 18 см; АВ2 = 15 см; б) А2В2 = 54 см, АА2 = 72 см.)
2. Задача № 33 із підручника (с. 21).
Теорема про відрізки паралельних прямих, які містяться між двома паралельними площинами
Можна запропонувати довести теорему самостійно. Наводимо запис, який можна зробити на дошці та в зошитах учнів.
Теорема.
Дано: a1 || a2; А1 I a1, В1 I a1, А2 I a2, А1А2 || В1В2.
Довести: А1А2 = В1В2 (рис. 67).
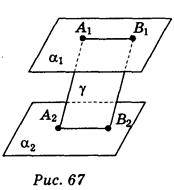
Проведемо площину у через прямі А1А2 і В1В2.
Чотирикутник А1В1В2А2 – паралелограм, бо А1А2 || В1В2 (за умовою), А1В1 || А2В2 (за теоремою про паралельність ліній перетину двох паралельних площин третьою площиною). Отже, А1А2 = В1В2.
Паралельні відрізки А1А2, В1B2, С1С2 розміщені між паралельними площинами a і b (рис. 68).
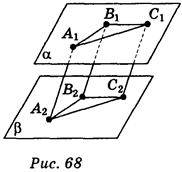
А) Визначте вид чотирикутників А1В1B2A2, В1С1C2В2, А1C1С2A2.
Б) Доведіть, що DА1В1С1 = DА2B2С2.
III. Домашнє завдання
§2, п. 12; контрольні запитання № 10, 11; задачі № 29, 32 (с. 21).
IV. Підведення підсумку уроку
1) Сформулюйте теорему про лінії перетину двох паралельних площин третьою площиною.
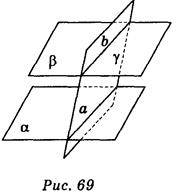
2) Дві паралельні площини a і b перетинаються площиною? по прямих а і b (рис. 69). Укажіть, які з тверджень правильні, а які – неправильні:
А) прямі а і b можуть бути мимобіжними;
Б) прямі а і b обов’язково паралельні;
В) пряма а паралельна площині b;
Г) будь-яка пряма, яка лежить у площині?, обов’язково перетинає обидві площини a і b.
3) Сформулюйте теорему про властивість паралельних відрізків, які лежать між паралельними площинами.
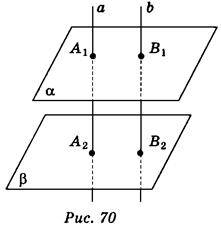
4) Площини a і b паралельні (рис. 70). Паралельні прямі а і b перетинають площину a в точках А1, В1, а площину b – в точках А2, В2. Укажіть, які з тверджень правильні, а які – неправильні:
А) А1А2 = В1B2;
Б) прямі А1B1 і А2В2 паралельні;
В) прямі А1В2 і А2В1 мимобіжні;
Г) прямі А1В2 і А2B1 перетинаються.
(1 votes, average: 5.00 out of 5)
Loading...